人教版七年级数学下册第八章 二元一次方程组8.2 消元——解二元一次方程组课件(2课时共58张)
文档属性
| 名称 | 人教版七年级数学下册第八章 二元一次方程组8.2 消元——解二元一次方程组课件(2课时共58张) |

|
|
| 格式 | zip | ||
| 文件大小 | 3.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-26 00:00:00 | ||
图片预览









文档简介
课件58张PPT。8.2消元——解二元一次方程组
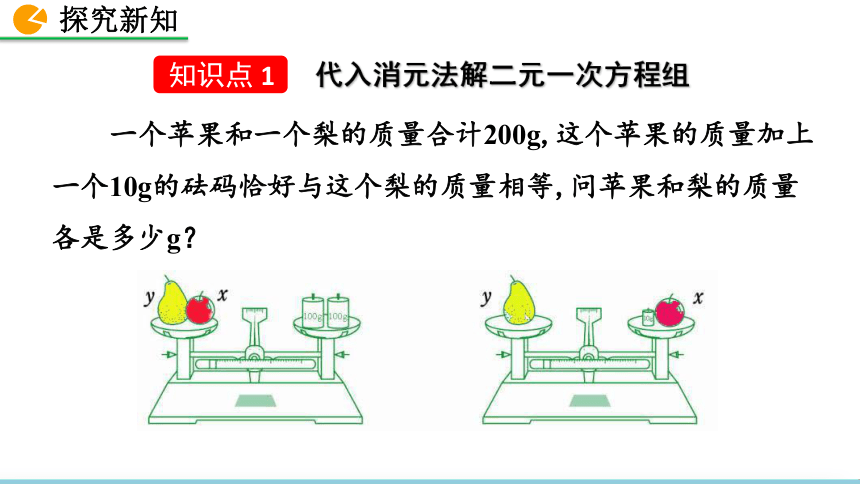
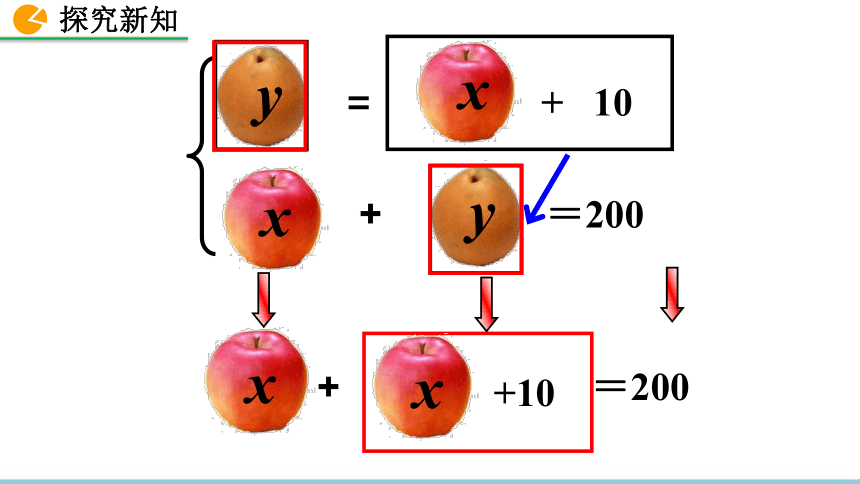
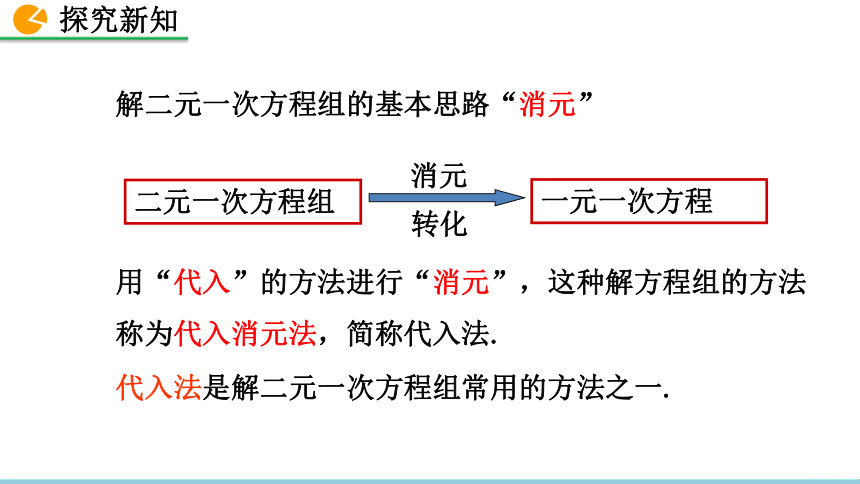
人教版 数学 七年级 下册代入消元法解二元一次方程组返回 篮球联赛中,每场比赛都要分出胜负,每队胜1场得2分,负1场得1分.某队在10场比赛中得到16分,那么这个队胜负场数分别是多少?(1)如果设胜的场数是x,则负的场数是10-x,可得一元一次方程;(2)如果设胜的场数是x ,负的场数是y,可得二元一次方程组那么怎样解这个二元一次方程组呢?1.掌握代入消元法解二元一次方程组的步骤.2.了解解二元一次方程组的基本思路.素养目标3.初步体会化归思想在数学学习中的运用. 一个苹果和一个梨的质量合计200g,这个苹果的质量加上一个10g的砝码恰好与这个梨的质量相等,问苹果和梨的质量各是多少g?代入消元法解二元一次方程组+=200xy=+ 10xy+10+=200xx x + y = 200y = x + 10(x+10)x +( x +10) = 200①②x = 95y = 105将未知数的个数由多化少,逐一解决的思想,叫做消元思想.转化求方程组解的过程叫做解方程组.解二元一次方程组的基本思路“消元”用“代入”的方法进行“消元”,这种解方程组的方法称为代入消元法,简称代入法. 代入法是解二元一次方程组常用的方法之一.解:由② ,得x=13 - 4y ③
将③代入① ,得 2(13 - 4y)+3y=16
26 –8y +3y =16,
-5y= -10, y=2将y=2代入③ ,得x=5.
所以原方程组的解是利用代入消元法解二元一次方程组
解二元一次方程组的步骤:
第一步:在已知方程组的两个方程中选择一个适当的方程,将它的某个未知数用含有另一个未知数的代数式表示出来.
第二步:把此代数式代入没有变形的一个方程中,可得一个一元一次方程.
第三步:解这个一元一次方程,得到一个未知数的值.
第四步:回代求出另一个未知数的值.
第五步:把方程组的解表示出来.
第六步:检验(口算或在草稿纸上进行笔算),即把求得的解代入每一个方程看是否成立.1. 用代入法解下列方程组:
解:把①代入②,得
3x+2( )=_
解这个方程,得x= .
把x= 代入①,得y= __
∴原方程组的解是2x-3822211 2-12x-522x-5-122例2 根据市场调查,某种消毒液的大瓶装(500 g)和小瓶装(250 g)两种产品的销售数量(按瓶计算)比为2:5.某厂每天生产这种消毒液22.5t,这些消毒液应该分装大、小瓶两种产品各多少瓶?分析:等量关系: (1)大瓶数 小瓶数 (2)大瓶所装消毒液 小瓶所装消毒液 总生产量. 利用二元一次方程组解答实际问题解:设这些消毒液应该分装x大瓶、y小瓶.根据题意可列方程组:解得:x=20000答:这些消毒液应该分装20000大瓶和50000小瓶.二元一次方程组
变形代入解得解得代入消元法的思路 用代入消元法解二元一次方程组时,尽量选取未知数系数的绝对值是1的方程进行变形;若未知数系数的绝对值都不是1,则选取系数的绝对值较小的方程变形. 累死我了真的?!他们各驮多少包裹?2.根据对话解答问题.解:设马驼了x个包裹,骆驼驼了y个包裹,由题意得:答:马驼了5个包裹,骆驼驼了7个包裹.解: ,
由①得,x=y+1 ③ ,
把③代入②得,y+1+3y=9,解得y=2,
把y=2代入x=y+1得x=3.
故原方程组的解为 . 巩固练习①②(2019?广州)解方程组:
1.二元一次方程组 的解是( ) D A.由①,得y=3x-2 ③,把③代入②,得3x=11-2(3x-2).B.由①,得 ③,把③代入②,得 .C.由②,得 ③,把③代入①,得 .D.把②代入 ①,得11-2y-y=2,(把3x看作一个整体)D 3.把下列方程分别用含x的式子表示y,含y的式子表示x:
(1)2x-y=3 (2)3x+2y=1解:(1)(2)解:由②变形得x=y+3③
将③代入① ,得3(y+3)+2y=143y+9+2y=14 将y=1代入②,得 x=45y=5,y=1
篮球联赛中,每场比赛都要分出胜负,胜一场得2分.负一场得1分,某队为了争取较好的名次,想在全部20场比赛中得到35分,那么这个队胜负场数分别是多少?解:设胜的场数是x,负的场数是y,可列方程组:
由①得y=20-x . ③
将③代入②,得 2x+20-x=35 .
解得 x=15.
将 x=15代入③得y=5.则这个方程组的解是
答:这个队胜15场,负5场.
①
②
李大叔去年承包了10亩地种植甲、乙两种蔬菜,共获利18000元,其中甲种蔬菜每亩获利2000元,乙种蔬菜每亩获利1500元,李大叔去年甲、乙两种蔬菜各种植了多少亩?解: 设甲、乙两种蔬菜各种植了x、y亩,依题意得:
x+y=10 ①
2000x+1500y=18000 ②
由①得y=10-x . ③
将③代入②,得 2000x+1500(10-x)=18000 .
解得 x=6.将x=6代入③,得y=4.
答:李大叔去年甲、乙两种蔬菜各种植了6亩、4亩.解二元一次方程组基本思路“消元”代入法解二元一次方程组的一般步骤加减法解二元一次方程组返回 一个长方形的周长是50cm,长比宽多5cm,设长为xcm,
宽为ycm,可列出的二元一次方程组是上面方程组的两个方程中,y的系数有什么关系?
利用这种关系你能发现新的消元方法吗?
2.熟练运用消元法解简单的二元一次方程组.1.掌握用加减消元法解二元一次方程组的步骤.素养目标3.培养学生的分析能力,能迅速根据所给的二元一次方程组,选择一种简单的方法解方程组.怎样解下面的二元一次方程组呢?①②加减法解二元一次方程组把②变形得:代入①,不就消去x了!把②变形得可以直接代入①呀!小明(3x+5y)+(2x-5y)= 21 + (-11)3x+5y = 21
2x-5y = -11按小丽的思路,你能消去
一个未知数吗?小丽分析: ①左边 + ②左边 = ①右边 + ②右边把x=2代入①,得y=3, x=23x+5y+2x-5y=10 5x+0y=10
5x=10 参考小丽的思路,怎样解下面的二元一次方程组呢?分析:观察方程组中的两个方程,未知数x的系数相等,即都是2.所以把这两个方程两边分别相减,就可以消去未知数x,得到一个一元一次方程.解:由 ②-①得:8y=-8
y=-1
把y =-1代入①,得
2x-5×(-1)=7
解得:x=1
所以原方程组的解是上面这些方程组的特点是什么?
解这类方程组的基本思路是什么?主要步骤有哪些?主要步骤: 特点:基本思路:写解求解加减二元一元.加减消元:消去一个元;分别求出两个未知数的值;写出原方程组的解.同一个未知数的系数相同或互为相反数.
例1 解下列二元一次方程组加减法解系数相等的二元一次方程组1.解方程组解:由②-①得:将x=5代入①得:15+2y=23y=4.2x=10x=5.解:把 ①+②得: 18x=10.8 x=0.6把x=0.6代入①,得:
3×0.6+10y=2.8解得:y=0.1例2 解方程组加减法解系数为相反数的二元一次方程组互为相反数相加 同一未知数的
系数 _
时,把两个方程
的两边分别 !解:由①+②得: 把x=2代入①,得:
y=3 x=25x=102.解二元一次方程组: 像上面这种解二元一次方程组的方法,叫做加减消元法,简称加减法. 当方程组中两个方程的某个未知数的系数互为相反数或相等时,可以把方程的两边分别相加(系数互为相反数)或相减(系数相等)来消去这个未知数,得到一个一元一次方程,进而求得二元一次方程组的解.例3 用加减法解方程组:①②解: ①×2得: 4x - 6y =8 ③ ③ + ②得:7x =14 x =2 把x =1代入①,得:y =0∴原方程组的解是加减法解找系数最小公倍数的二元一次方程组 同一未知数的系数 时,利等
式的性质,使得未知数的系数 .
不相等也不互为相反数相等或互为相反数 3.用加减法解方程组:①×3得:所以原方程组的解是解: ③-④得: y=2 把y=2代入①,
解得: x=3 ②×2得:6x+9y=36 ③6x+8y=34 ④解: ②×4得:所以原方程组的解为①4.解方程组:②③ ①+③得:7x = 35,解得:x = 5.把x = 5代入②得,y = 1.4x-4y=16例4 2台大收割机和5台小收割机均工作2h共收割小麦3.6 hm2,3台大收割机和2台小收割机同时工作5h共收割小麦8 hm2.1台大收割机和1台小收割机每小时各收割小麦多少公顷?
分析:题目中存在的两个等量关系:
2×(2台大收割量+5台小收割量)=______
5×(3台大收割量+2台小收割量)=______3.6hm28hm2列二元一次方程组解实际问题3.6
整理,得解:设一台大收割机和一台小收割机每小时各收割小麦x hm2和y hm2.根据题意,得
②-①,得 __________
解得 x=_______
把x=_____ 代入①,得y=_______
∴这个方程组的解为
答:一台大收割机和一台小收割机每小时分别收割小麦0.4hm2和0.2hm24x+10y15x+10y 811x=4.40.40.40.20.20.4①②
利用二元一次方程组解决实际问题的基本步骤是:
(1)依题意,找________关系;
(2)根据等量关系设_______;
(3)列__________;
(4)解__________;
(5)检验并作答.等量关系未知数方程组方程组
5.一条船顺流航行,每小时行20km,逆流航行,每小时行16km,求轮船在静水中的速度与水的速度.解:设轮船在静水中的速度为xkm/h,水流的速度为ykm/h
由题意得:
解得
答:轮船在静水中的速度为18km/h,水流的速度为2km/h.
1.(2019?贺州)已知方程组 ,则2x+6y的值是( )
A.﹣2 B.2 C.﹣4 D.4 巩固练习2.(2019?菏泽)已知 是方程组 的解 ,
则a+b的值是( )
A.﹣1 B.1 C.﹣5 D.5 CA1.方程组 的解是 .①②2. 用加减法解方程组6x+7y=-19①6x-5y=17 ②应用( )A.①-②消去y B.①-②消去xC. ②- ①消去常数项D. 以上都不对B (1)(2)解:①-②得2x=4,x=2
把x=2代入②得
2+2y=4,2y=2
y=1
所以方程组的解是解:①+②得4x=12,x=3
把x=3代入②得
3+y=4,y=1
所以方程组的解是3.解方程组4.已知x、y满足方程组 求代数式x-y的值.解:
②-①得2x-2y=-1-5,
得x-y=-3.①
② 解方程组 解:由① + ②,得 4(x+y)=36 所以 x+y=9 ③由① - ②,得 6(x-y)=24 所以 x-y=4 ④解由③④组成的方程组解得 2辆大卡车和5辆小卡车工作2小时可运送垃圾36吨,3辆大卡车和2辆小卡车工作5小时可运输垃圾80 吨, 那么1辆大卡车和1辆小卡车每小时各运多少吨垃圾?解:设1辆大卡车和1辆小卡车每小时各运x吨和y吨垃圾.②-①得 11x=44,解得x=4.将x=4代入①可得y=2.因此这个方程组的解 .答:1辆大卡车和1辆小卡车每小时各运4吨和2吨垃圾.解二元一次方程组基本思路“消元”加减法解二元一次方程组的一般步骤课后作业作业
内容教材作业从课后习题中选取自主安排配套练习册练习
人教版 数学 七年级 下册代入消元法解二元一次方程组返回 篮球联赛中,每场比赛都要分出胜负,每队胜1场得2分,负1场得1分.某队在10场比赛中得到16分,那么这个队胜负场数分别是多少?(1)如果设胜的场数是x,则负的场数是10-x,可得一元一次方程;(2)如果设胜的场数是x ,负的场数是y,可得二元一次方程组那么怎样解这个二元一次方程组呢?1.掌握代入消元法解二元一次方程组的步骤.2.了解解二元一次方程组的基本思路.素养目标3.初步体会化归思想在数学学习中的运用. 一个苹果和一个梨的质量合计200g,这个苹果的质量加上一个10g的砝码恰好与这个梨的质量相等,问苹果和梨的质量各是多少g?代入消元法解二元一次方程组+=200xy=+ 10xy+10+=200xx x + y = 200y = x + 10(x+10)x +( x +10) = 200①②x = 95y = 105将未知数的个数由多化少,逐一解决的思想,叫做消元思想.转化求方程组解的过程叫做解方程组.解二元一次方程组的基本思路“消元”用“代入”的方法进行“消元”,这种解方程组的方法称为代入消元法,简称代入法. 代入法是解二元一次方程组常用的方法之一.解:由② ,得x=13 - 4y ③
将③代入① ,得 2(13 - 4y)+3y=16
26 –8y +3y =16,
-5y= -10, y=2将y=2代入③ ,得x=5.
所以原方程组的解是利用代入消元法解二元一次方程组
解二元一次方程组的步骤:
第一步:在已知方程组的两个方程中选择一个适当的方程,将它的某个未知数用含有另一个未知数的代数式表示出来.
第二步:把此代数式代入没有变形的一个方程中,可得一个一元一次方程.
第三步:解这个一元一次方程,得到一个未知数的值.
第四步:回代求出另一个未知数的值.
第五步:把方程组的解表示出来.
第六步:检验(口算或在草稿纸上进行笔算),即把求得的解代入每一个方程看是否成立.1. 用代入法解下列方程组:
解:把①代入②,得
3x+2( )=_
解这个方程,得x= .
把x= 代入①,得y= __
∴原方程组的解是2x-3822211 2-12x-522x-5-122例2 根据市场调查,某种消毒液的大瓶装(500 g)和小瓶装(250 g)两种产品的销售数量(按瓶计算)比为2:5.某厂每天生产这种消毒液22.5t,这些消毒液应该分装大、小瓶两种产品各多少瓶?分析:等量关系: (1)大瓶数 小瓶数 (2)大瓶所装消毒液 小瓶所装消毒液 总生产量. 利用二元一次方程组解答实际问题解:设这些消毒液应该分装x大瓶、y小瓶.根据题意可列方程组:解得:x=20000答:这些消毒液应该分装20000大瓶和50000小瓶.二元一次方程组
变形代入解得解得代入消元法的思路 用代入消元法解二元一次方程组时,尽量选取未知数系数的绝对值是1的方程进行变形;若未知数系数的绝对值都不是1,则选取系数的绝对值较小的方程变形. 累死我了真的?!他们各驮多少包裹?2.根据对话解答问题.解:设马驼了x个包裹,骆驼驼了y个包裹,由题意得:答:马驼了5个包裹,骆驼驼了7个包裹.解: ,
由①得,x=y+1 ③ ,
把③代入②得,y+1+3y=9,解得y=2,
把y=2代入x=y+1得x=3.
故原方程组的解为 . 巩固练习①②(2019?广州)解方程组:
1.二元一次方程组 的解是( ) D A.由①,得y=3x-2 ③,把③代入②,得3x=11-2(3x-2).B.由①,得 ③,把③代入②,得 .C.由②,得 ③,把③代入①,得 .D.把②代入 ①,得11-2y-y=2,(把3x看作一个整体)D 3.把下列方程分别用含x的式子表示y,含y的式子表示x:
(1)2x-y=3 (2)3x+2y=1解:(1)(2)解:由②变形得x=y+3③
将③代入① ,得3(y+3)+2y=143y+9+2y=14 将y=1代入②,得 x=45y=5,y=1
篮球联赛中,每场比赛都要分出胜负,胜一场得2分.负一场得1分,某队为了争取较好的名次,想在全部20场比赛中得到35分,那么这个队胜负场数分别是多少?解:设胜的场数是x,负的场数是y,可列方程组:
由①得y=20-x . ③
将③代入②,得 2x+20-x=35 .
解得 x=15.
将 x=15代入③得y=5.则这个方程组的解是
答:这个队胜15场,负5场.
①
②
李大叔去年承包了10亩地种植甲、乙两种蔬菜,共获利18000元,其中甲种蔬菜每亩获利2000元,乙种蔬菜每亩获利1500元,李大叔去年甲、乙两种蔬菜各种植了多少亩?解: 设甲、乙两种蔬菜各种植了x、y亩,依题意得:
x+y=10 ①
2000x+1500y=18000 ②
由①得y=10-x . ③
将③代入②,得 2000x+1500(10-x)=18000 .
解得 x=6.将x=6代入③,得y=4.
答:李大叔去年甲、乙两种蔬菜各种植了6亩、4亩.解二元一次方程组基本思路“消元”代入法解二元一次方程组的一般步骤加减法解二元一次方程组返回 一个长方形的周长是50cm,长比宽多5cm,设长为xcm,
宽为ycm,可列出的二元一次方程组是上面方程组的两个方程中,y的系数有什么关系?
利用这种关系你能发现新的消元方法吗?
2.熟练运用消元法解简单的二元一次方程组.1.掌握用加减消元法解二元一次方程组的步骤.素养目标3.培养学生的分析能力,能迅速根据所给的二元一次方程组,选择一种简单的方法解方程组.怎样解下面的二元一次方程组呢?①②加减法解二元一次方程组把②变形得:代入①,不就消去x了!把②变形得可以直接代入①呀!小明(3x+5y)+(2x-5y)= 21 + (-11)3x+5y = 21
2x-5y = -11按小丽的思路,你能消去
一个未知数吗?小丽分析: ①左边 + ②左边 = ①右边 + ②右边把x=2代入①,得y=3, x=23x+5y+2x-5y=10 5x+0y=10
5x=10 参考小丽的思路,怎样解下面的二元一次方程组呢?分析:观察方程组中的两个方程,未知数x的系数相等,即都是2.所以把这两个方程两边分别相减,就可以消去未知数x,得到一个一元一次方程.解:由 ②-①得:8y=-8
y=-1
把y =-1代入①,得
2x-5×(-1)=7
解得:x=1
所以原方程组的解是上面这些方程组的特点是什么?
解这类方程组的基本思路是什么?主要步骤有哪些?主要步骤: 特点:基本思路:写解求解加减二元一元.加减消元:消去一个元;分别求出两个未知数的值;写出原方程组的解.同一个未知数的系数相同或互为相反数.
例1 解下列二元一次方程组加减法解系数相等的二元一次方程组1.解方程组解:由②-①得:将x=5代入①得:15+2y=23y=4.2x=10x=5.解:把 ①+②得: 18x=10.8 x=0.6把x=0.6代入①,得:
3×0.6+10y=2.8解得:y=0.1例2 解方程组加减法解系数为相反数的二元一次方程组互为相反数相加 同一未知数的
系数 _
时,把两个方程
的两边分别 !解:由①+②得: 把x=2代入①,得:
y=3 x=25x=102.解二元一次方程组: 像上面这种解二元一次方程组的方法,叫做加减消元法,简称加减法. 当方程组中两个方程的某个未知数的系数互为相反数或相等时,可以把方程的两边分别相加(系数互为相反数)或相减(系数相等)来消去这个未知数,得到一个一元一次方程,进而求得二元一次方程组的解.例3 用加减法解方程组:①②解: ①×2得: 4x - 6y =8 ③ ③ + ②得:7x =14 x =2 把x =1代入①,得:y =0∴原方程组的解是加减法解找系数最小公倍数的二元一次方程组 同一未知数的系数 时,利等
式的性质,使得未知数的系数 .
不相等也不互为相反数相等或互为相反数 3.用加减法解方程组:①×3得:所以原方程组的解是解: ③-④得: y=2 把y=2代入①,
解得: x=3 ②×2得:6x+9y=36 ③6x+8y=34 ④解: ②×4得:所以原方程组的解为①4.解方程组:②③ ①+③得:7x = 35,解得:x = 5.把x = 5代入②得,y = 1.4x-4y=16例4 2台大收割机和5台小收割机均工作2h共收割小麦3.6 hm2,3台大收割机和2台小收割机同时工作5h共收割小麦8 hm2.1台大收割机和1台小收割机每小时各收割小麦多少公顷?
分析:题目中存在的两个等量关系:
2×(2台大收割量+5台小收割量)=______
5×(3台大收割量+2台小收割量)=______3.6hm28hm2列二元一次方程组解实际问题3.6
整理,得解:设一台大收割机和一台小收割机每小时各收割小麦x hm2和y hm2.根据题意,得
②-①,得 __________
解得 x=_______
把x=_____ 代入①,得y=_______
∴这个方程组的解为
答:一台大收割机和一台小收割机每小时分别收割小麦0.4hm2和0.2hm24x+10y15x+10y 811x=4.40.40.40.20.20.4①②
利用二元一次方程组解决实际问题的基本步骤是:
(1)依题意,找________关系;
(2)根据等量关系设_______;
(3)列__________;
(4)解__________;
(5)检验并作答.等量关系未知数方程组方程组
5.一条船顺流航行,每小时行20km,逆流航行,每小时行16km,求轮船在静水中的速度与水的速度.解:设轮船在静水中的速度为xkm/h,水流的速度为ykm/h
由题意得:
解得
答:轮船在静水中的速度为18km/h,水流的速度为2km/h.
1.(2019?贺州)已知方程组 ,则2x+6y的值是( )
A.﹣2 B.2 C.﹣4 D.4 巩固练习2.(2019?菏泽)已知 是方程组 的解 ,
则a+b的值是( )
A.﹣1 B.1 C.﹣5 D.5 CA1.方程组 的解是 .①②2. 用加减法解方程组6x+7y=-19①6x-5y=17 ②应用( )A.①-②消去y B.①-②消去xC. ②- ①消去常数项D. 以上都不对B (1)(2)解:①-②得2x=4,x=2
把x=2代入②得
2+2y=4,2y=2
y=1
所以方程组的解是解:①+②得4x=12,x=3
把x=3代入②得
3+y=4,y=1
所以方程组的解是3.解方程组4.已知x、y满足方程组 求代数式x-y的值.解:
②-①得2x-2y=-1-5,
得x-y=-3.①
② 解方程组 解:由① + ②,得 4(x+y)=36 所以 x+y=9 ③由① - ②,得 6(x-y)=24 所以 x-y=4 ④解由③④组成的方程组解得 2辆大卡车和5辆小卡车工作2小时可运送垃圾36吨,3辆大卡车和2辆小卡车工作5小时可运输垃圾80 吨, 那么1辆大卡车和1辆小卡车每小时各运多少吨垃圾?解:设1辆大卡车和1辆小卡车每小时各运x吨和y吨垃圾.②-①得 11x=44,解得x=4.将x=4代入①可得y=2.因此这个方程组的解 .答:1辆大卡车和1辆小卡车每小时各运4吨和2吨垃圾.解二元一次方程组基本思路“消元”加减法解二元一次方程组的一般步骤课后作业作业
内容教材作业从课后习题中选取自主安排配套练习册练习
