人教高中数学必修二2.2.2平面与平面平行的判定定理 教案
文档属性
| 名称 | 人教高中数学必修二2.2.2平面与平面平行的判定定理 教案 |

|
|
| 格式 | zip | ||
| 文件大小 | 158.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-27 00:00:00 | ||
图片预览

文档简介
平面与平面平行的判定
学习内容分析
本节课选自《普通高中标准实验教科书—数学必修二》(人教版)第二章点、直线、平面之间的位置关系第二节直线、平面平行的判定及其性质,主要研究平面与平面平行的判定方法。根据课标要求和学生情况,本节课分为四个课时,今天学习第二课时。本节课是建立在学习空间中直线与直线、直线与平面位置关系基础上的一节课,并为后续学习平面与平面平行性质奠定基础。
教材首先通过观察三角板所在平面与桌面位置关系引入课题,然后将两个平面平行的问题转化为一个平面内的直线与另一个平面平行的问题,体现数学中的转化思想。接着根据两个平面中直线的关系探究两个平面的位置关系,体现分类讨论思想,培养了学生自主探究的能力。
学习者分析
从已有知识来看,学生已经学习了空间点、直线、平面之间的位置关系,掌握了直线与平面平行的判定定理;
从已有经验来看,学生已经掌握了分类讨论、转化的思想;
从已有能力来看,学生已经具有了自主探索、简单的空间想象能力。
但对于高二学生来说,他们初次接触空间立体几何,对于空间的部分问题仍有较大困惑,空间想象能力还不是很强。
教学目标
知识与技能目标:
①通过直观感知,操作确认,归纳出平面与平面平行的判定定理;
②理解并掌握两平面平行的判定方法;
③能够运用两个平面平行的判定方法解决相关问题。
过程与方法目标:
①通过观察相关模型以及实物,培养分析、归纳的能力;
②在探究平面与平面平行判定定理的过程中,体会分类讨论、转化的思想。
情感、态度与价值观目标:
在发现中学习,提高学习数学的积极性,培养主动探究、合作交流的意识
教学重难点
教学重点:两个平面平行的判定;
教学难点:探究平面与平面平行的判定定理以及应用判定定理解决相关问题。
教学过程
复习旧知,导入新课
问题一:
①平面几何中,判定两直线平行有哪几种方法?
②直线与平面平行有哪些方法?
③平面与平面有哪些位置关系?
师生活动:教师提出问题,引导学生进行回答。
【设计意图】通过回顾两直线平行、直线与平面平行的判定方法引出平面与平面之间的关系,从而引入课题:平面与平面平行的判定。在探索平面与平面平行的判定定理以及应用定理进行证明过程中,仍然要用到直线平行以及直线与平面平行的判定。在导入新课前对此类的复习,有助于学生回忆以及应用。
自主探索,归纳定理
两个平面平行的定义:如果两个平面没有公共点,那么这两个平面互相平行,也叫作平行平面。如果平面平行于平面,我们把它记作。
判定平面与平面平行的方法:
判定方法一:定义法
如果两个平面没有交点,那么这两个平面互相平行。(若两个平面存在交点,则由公理三,它们有且只有一条过该点的直线,此时可以将平面与平面平行问题转化为直线与平面平行问题。)
问题二:
①如果平面内的一条直线平行于平面,那么平面平行于平面么?
②如果平面内的两条直线平行于平面,那么平面平行于平面么?
【师生活动】教师提出问题,引导学生思考并回答。
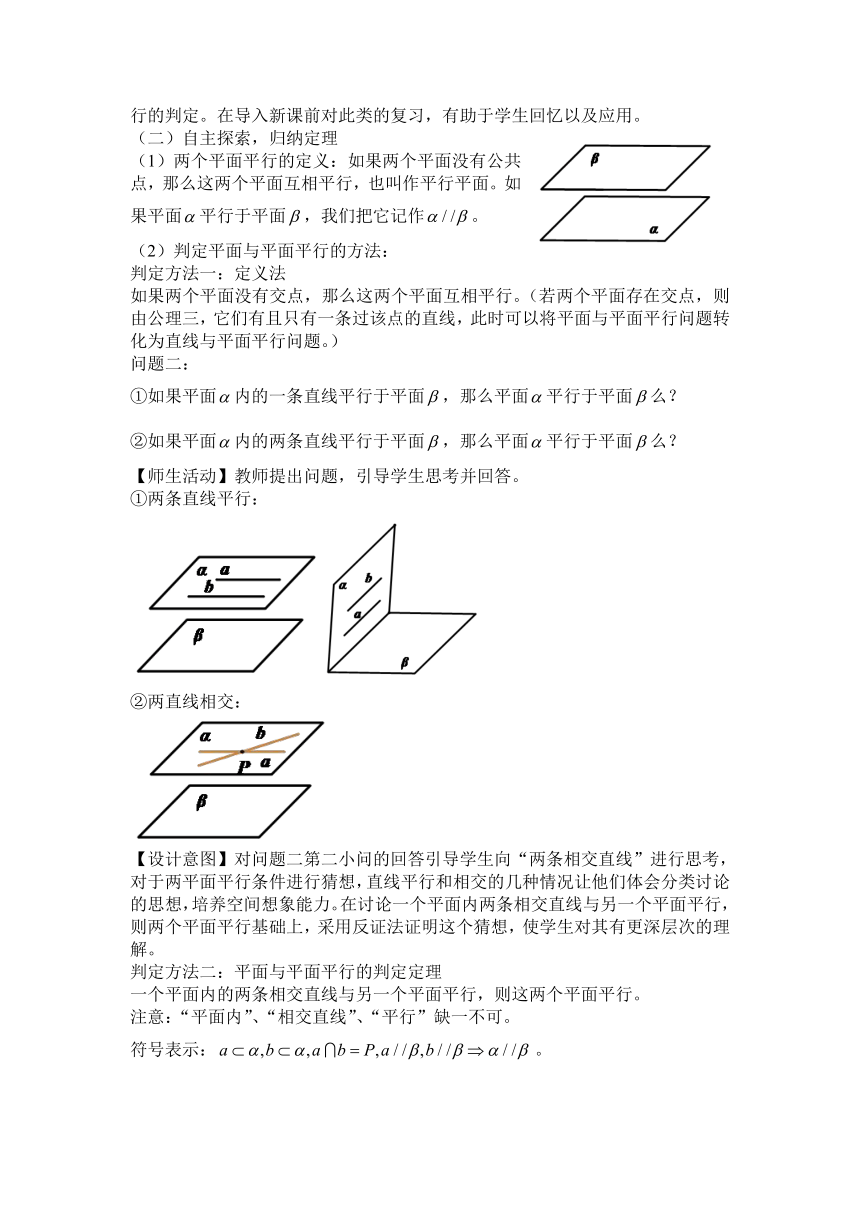
①两条直线平行:
②两直线相交:
【设计意图】对问题二第二小问的回答引导学生向“两条相交直线”进行思考,对于两平面平行条件进行猜想,直线平行和相交的几种情况让他们体会分类讨论的思想,培养空间想象能力。在讨论一个平面内两条相交直线与另一个平面平行,则两个平面平行基础上,采用反证法证明这个猜想,使学生对其有更深层次的理解。
判定方法二:平面与平面平行的判定定理
一个平面内的两条相交直线与另一个平面平行,则这两个平面平行。
注意:“平面内”、“相交直线”、“平行”缺一不可。
符号表示:。
利用反证法证明定理:
假设平面
判定方法三:一个平面内的两条相交直线分别与另一个平面内的两条相交直线平行,则这两个平面平行。
巩固练习,加深理解
例1:判断下列命题是否正确,请说明理由。
①若平面内的两条直线分别与平面平行,则与平行;
②若平面内有无数条直线分别与平面平行,则与平行;
③一个平面内两条不平行的直线都平行于平面,则与平行;
④如果一个平面内的任何直线都平行于另一个平面,那么这两个平面平行;
⑤如果一个平面内的一条直线平行于另一个平面,那么这两个平面平行。
例2:。
例3:
例4:
复习小结,深化内涵
1、平面与平面平行的判定:
定义法;
判定定理:如果一个平面内的两条相交直线平行于另一个平面,那么这两个平面平行。
定理:如果一个平面内的两条相交直线分别与另一个平面内的两条相交直线平行,那么这两个平面平行。
平面平行的传递性。
思想方法:
面面平行——线面平行——线线平行
布置作业
板书设计
2.2.2平面与平面平行的判定 判定定理:如果一个平面内的两条相交直线平行于另一个平面,那么这两个平面平行。 (1)反证法: (2)例1:
学习内容分析
本节课选自《普通高中标准实验教科书—数学必修二》(人教版)第二章点、直线、平面之间的位置关系第二节直线、平面平行的判定及其性质,主要研究平面与平面平行的判定方法。根据课标要求和学生情况,本节课分为四个课时,今天学习第二课时。本节课是建立在学习空间中直线与直线、直线与平面位置关系基础上的一节课,并为后续学习平面与平面平行性质奠定基础。
教材首先通过观察三角板所在平面与桌面位置关系引入课题,然后将两个平面平行的问题转化为一个平面内的直线与另一个平面平行的问题,体现数学中的转化思想。接着根据两个平面中直线的关系探究两个平面的位置关系,体现分类讨论思想,培养了学生自主探究的能力。
学习者分析
从已有知识来看,学生已经学习了空间点、直线、平面之间的位置关系,掌握了直线与平面平行的判定定理;
从已有经验来看,学生已经掌握了分类讨论、转化的思想;
从已有能力来看,学生已经具有了自主探索、简单的空间想象能力。
但对于高二学生来说,他们初次接触空间立体几何,对于空间的部分问题仍有较大困惑,空间想象能力还不是很强。
教学目标
知识与技能目标:
①通过直观感知,操作确认,归纳出平面与平面平行的判定定理;
②理解并掌握两平面平行的判定方法;
③能够运用两个平面平行的判定方法解决相关问题。
过程与方法目标:
①通过观察相关模型以及实物,培养分析、归纳的能力;
②在探究平面与平面平行判定定理的过程中,体会分类讨论、转化的思想。
情感、态度与价值观目标:
在发现中学习,提高学习数学的积极性,培养主动探究、合作交流的意识
教学重难点
教学重点:两个平面平行的判定;
教学难点:探究平面与平面平行的判定定理以及应用判定定理解决相关问题。
教学过程
复习旧知,导入新课
问题一:
①平面几何中,判定两直线平行有哪几种方法?
②直线与平面平行有哪些方法?
③平面与平面有哪些位置关系?
师生活动:教师提出问题,引导学生进行回答。
【设计意图】通过回顾两直线平行、直线与平面平行的判定方法引出平面与平面之间的关系,从而引入课题:平面与平面平行的判定。在探索平面与平面平行的判定定理以及应用定理进行证明过程中,仍然要用到直线平行以及直线与平面平行的判定。在导入新课前对此类的复习,有助于学生回忆以及应用。
自主探索,归纳定理
两个平面平行的定义:如果两个平面没有公共点,那么这两个平面互相平行,也叫作平行平面。如果平面平行于平面,我们把它记作。
判定平面与平面平行的方法:
判定方法一:定义法
如果两个平面没有交点,那么这两个平面互相平行。(若两个平面存在交点,则由公理三,它们有且只有一条过该点的直线,此时可以将平面与平面平行问题转化为直线与平面平行问题。)
问题二:
①如果平面内的一条直线平行于平面,那么平面平行于平面么?
②如果平面内的两条直线平行于平面,那么平面平行于平面么?
【师生活动】教师提出问题,引导学生思考并回答。
①两条直线平行:
②两直线相交:
【设计意图】对问题二第二小问的回答引导学生向“两条相交直线”进行思考,对于两平面平行条件进行猜想,直线平行和相交的几种情况让他们体会分类讨论的思想,培养空间想象能力。在讨论一个平面内两条相交直线与另一个平面平行,则两个平面平行基础上,采用反证法证明这个猜想,使学生对其有更深层次的理解。
判定方法二:平面与平面平行的判定定理
一个平面内的两条相交直线与另一个平面平行,则这两个平面平行。
注意:“平面内”、“相交直线”、“平行”缺一不可。
符号表示:。
利用反证法证明定理:
假设平面
判定方法三:一个平面内的两条相交直线分别与另一个平面内的两条相交直线平行,则这两个平面平行。
巩固练习,加深理解
例1:判断下列命题是否正确,请说明理由。
①若平面内的两条直线分别与平面平行,则与平行;
②若平面内有无数条直线分别与平面平行,则与平行;
③一个平面内两条不平行的直线都平行于平面,则与平行;
④如果一个平面内的任何直线都平行于另一个平面,那么这两个平面平行;
⑤如果一个平面内的一条直线平行于另一个平面,那么这两个平面平行。
例2:。
例3:
例4:
复习小结,深化内涵
1、平面与平面平行的判定:
定义法;
判定定理:如果一个平面内的两条相交直线平行于另一个平面,那么这两个平面平行。
定理:如果一个平面内的两条相交直线分别与另一个平面内的两条相交直线平行,那么这两个平面平行。
平面平行的传递性。
思想方法:
面面平行——线面平行——线线平行
布置作业
板书设计
2.2.2平面与平面平行的判定 判定定理:如果一个平面内的两条相交直线平行于另一个平面,那么这两个平面平行。 (1)反证法: (2)例1:
