人教版七年级数学下册第五章 相交线与平行线5.3.1平行线的性质课件(2课时共49张)
文档属性
| 名称 | 人教版七年级数学下册第五章 相交线与平行线5.3.1平行线的性质课件(2课时共49张) |  | |
| 格式 | zip | ||
| 文件大小 | 2.3MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-26 16:57:26 | ||
图片预览







文档简介
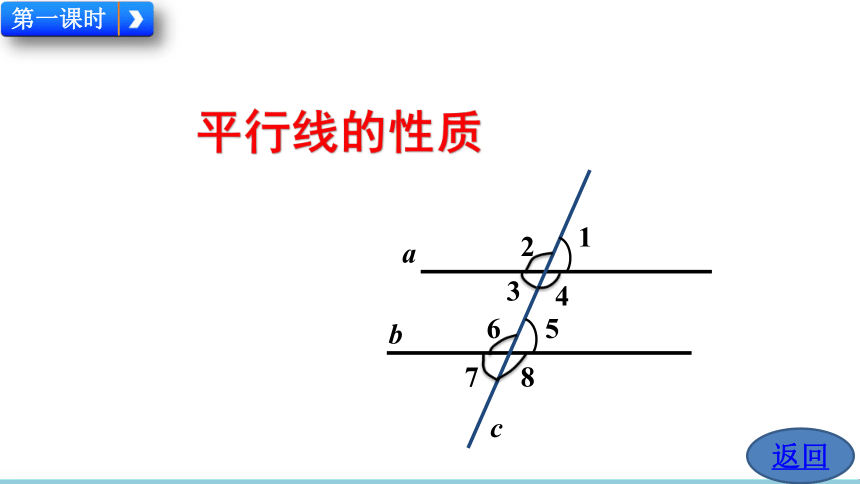
课件49张PPT。5.3 平行线的性质
5.3.1 平行线的性质人教版 数学 七年级 下册平行线的性质返回【思考】根据同位角相等可以判定两直线平行,反过来如果两直线平行,同位角之间有什么关系呢?内错角、同旁内角之间又有什么关系呢?
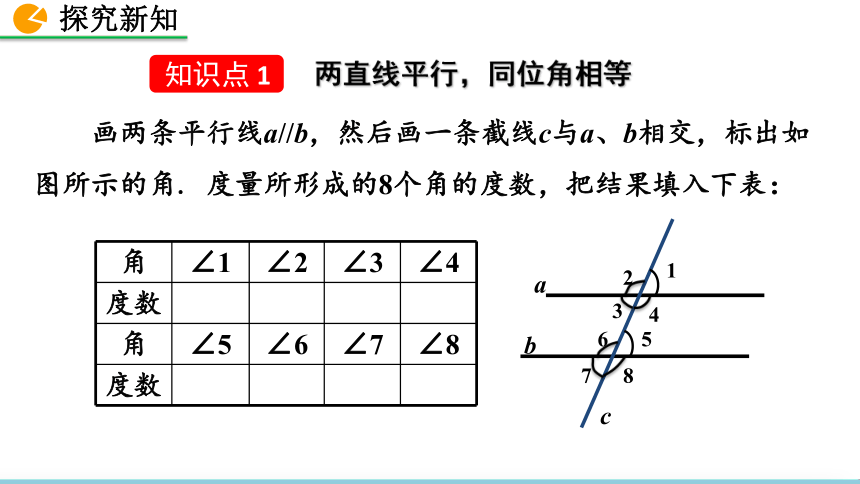
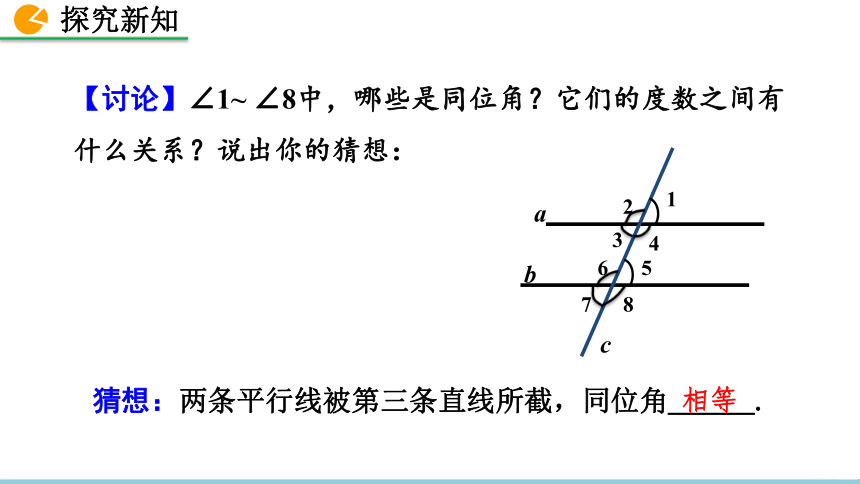
1. 掌握平行线的性质,会运用两条直线是平行关系判断角相等或互补.2. 能够根据平行线的性质进行简单的推理.素养目标3. 区分平行线的性质和判定的关系,培养学生逆向思维的能力. 画两条平行线a//b,然后画一条截线c与a、b相交,标出如图所示的角. 度量所形成的8个角的度数,把结果填入下表:【讨论】∠1~ ∠8中,哪些是同位角?它们的度数之间有什么关系?说出你的猜想: 猜想:两条平行线被第三条直线所截,同位角___.
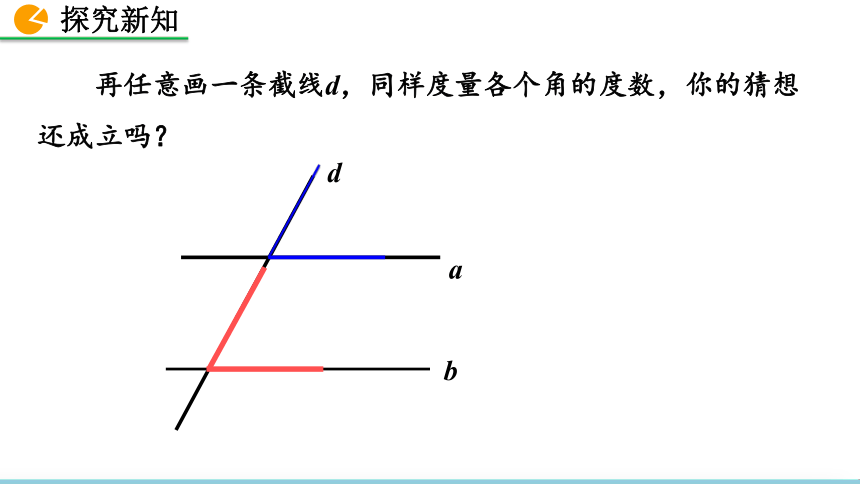
相等abd 再任意画一条截线d,同样度量各个角的度数,你的猜想还成立吗?如果两直线不平行,上述结论还成立吗?一般地,平行线具有如下性质:性质1:两条平行线被第三条直线所截,同位角相等.∴∠1=∠2
(两直线平行,同位角相等)∵a∥b(已知)几何语言:简单说成:两直线平行,同位角相等. 例1 如图,D是AB上一点,E是AC上一点,∠ADE=60°,∠B=60°, ∠AED=40°.(1)DE和BC平行吗?为什么? (2)∠C是多少度?为什么? 答:(1)DE∥BC,
∵∠ADE=60°,∠B=60°,∴∠ADE= ∠B.
∴DE∥BC ( )同位角相等,两直线平行(2) ∠C =40°.
( )
∵∠AED=40°,∴∠C =40°.两直线平行,同位角相等∵DE∥BC ,∴∠C = ∠AED.1. 如图所示,∠1=70°,若m∥n,则∠2= .
2.如图所示,直线m∥n,∠1=70°,∠2=30°,则∠A等于 ( )
A. 30° B. 35°
C. 40° D. 50°70°Cnm21 在上一节中,我们利用“同位角相等,两直线平行”推出了“内错角相等,两直线平行线”,类似地,已知两直线平行,同位角相等,能否得到内错角之间的数量关系? 如图,已知a//b,那么?2与?3相等吗?为什么?解:∵ a∥b(已知),
∴∠1=∠2(两直线平行,同位角相等).
又∵ ∠1=∠3(对顶角相等),
∴ ∠2=∠3(等量代换).性质2:两条平行线被第三条直线所截,内错角相等. ∴∠2=∠3
(两直线平行,内错角相等)∵a∥b(已知)几何语言:简单说成:两直线平行,内错角相等.例2 如图,已知直线a∥b,∠1 = 50°, 求∠2的度数.abc12∴∠ 2= 50° (等量代换)解:∵ a∥b(已知)∴∠ 1= ∠ 2
(两直线平行,内错角相等)又∵∠ 1 = 50° (已知)利用“两直线平行,内错角相等”求角的度数3.如图所示,AC∥BD,∠A=70°,∠C=50°,则
∠1= ,∠2= ,∠3= .70°50°60°如图,已知a//b,那么?2与?4有什么关系呢?为什么?解: ∵a//b (已知), ∴? 1= ? 2(两直线平行,同位角相等).∵ ? 1+ ? 4=180°(邻补角的性质),∴? 2+ ? 4=180°(等量代换).类似地,已知两直线平行,能否得到同旁内角之间的数量关系? 性质3:两条平行线被第三条直线所截,同旁内角互补. ∴∠2+∠4=180 °
(两直线平行,同旁内角互补)∵a∥b(已知)几何语言:简单说成:两直线平行,同旁内角互补. 例3 如图是一块梯形铁片的残余部分,量得∠A=100°,∠B=115°,梯形的另外两个角的度数分别是多少?解:∵梯形上、下底互相平行,
∴ ∠A与∠D互补, ∠B与∠C互补.∴梯形的另外两个角分别是80°、65°.于是∠D=180 °-∠A=180°-100°=80°
∠C= 180 °-∠B=180°-115°=65°4.如图所示,直线a∥b,直线l与a,b分别相交于A、B两点,过点A作直线l的垂线交直线b于点C,若∠1=58°,则∠2的度数为( )
A. 58° B. 42°
C. 32° D. 28°C(2019?日照)如图,将一块三角尺的直角顶点放在直尺的一边上,当∠1=35°时,∠2的度数为( )
A.35° B.45°
C.55° D.65°巩固练习C
1.如图所示,直线a∥b,直线c与直线a,b相交,若∠1=56°,则∠2等于 ( )
A. 24°
B. 34°
C. 56°
D. 124°C2.如图所示,AB∥CD,直线EF与AB,CD分别交于点M,N,过点N的直线GH与AB交于点P,则下列结论错误的是( )
A. ∠EMB=∠END
B. ∠BMN=∠MNC
C. ∠CNH=∠BPG
D. ∠DNG=∠AMED3. 如图所示,直线a∥b,点B在直线a上,AB⊥BC,若
∠1=38°,则∠2的度数为 ( )
A. 38° B. 52° C. 76° D. 142°B4.如图所示,AB∥CD,∠E=40°,∠A=110°,则∠C的度数为( )
A. 60° B. 80° C. 75° D. 70°D5. 如图所示,直线a∥b,Rt△ABC的直角顶点C在直线b上,∠1=20°,则∠2= °. 70解: ∵ AB∥DE( )
∴∠A= ______ ( )
∵AC∥DF( )
∴∠D+ _______=180o ( )
∴∠A+∠D=180o( ) 有这样一道题:如图,若AB∥DE , AC∥DF,试说明∠A+∠D=180o.请补全下面的解答过程,括号内填写依据.已知∠CPD两直线平行,同位角相等已知∠CPD两直线平行,同旁内角互补等量代换 如图,潜望镜中的两面镜子是互相平行放置的,光线经过镜子反射时,∠1=∠2,∠3=∠4,∠2和∠3有什么关系?为什么进入潜望镜的光线和离开潜望镜的光线是平行的?解:∠2=∠3,
∵两直线平行,内错角相等;∴∠2=∠3,∵∠1=∠2,∠3=∠4,
∴∠1=∠2=∠3=∠4,∴ ∠5=∠6,
∴进入潜望镜的光线和离开潜望镜
的光线平行.同位角相等
内错角相等
同旁内角互补两直线平行判定性质平行线的判定与性质的综合应用返回 一辆汽车沿AB方向行驶,在C处拐了一个弯,行驶一段时间到D处又一次改变方向,此时车子与原来的方向是否一致?为什么?2. 进一步熟悉平行线的判定方法和性质.1. 分清平行线的性质和判定;已知平行用性质,要证平行用判定 .素养目标3. 能够综合运用平行线性质和判定进行推理证明.证明:∵ AD ∥BC(已知)
∴ ∠A+∠B=180°( )
∵ ∠AEF=∠B(已知)
∴ ∠A+∠AEF=180°(等量代换)
∴ AD∥EF( )
【思考】在填写依据时要注意什么问题?两直线平行,同旁内角互补同旁内角互补,两直线平行如图,已知:AD∥BC, ∠AEF=∠B,
求证:AD∥EF.1.如图,AB∥EF,∠ECD=∠E,则∠A=∠ECD.
理由如下:
∵∠ECD=∠E,
∴CD∥EF( )
又AB∥EF,
∴CD∥AB( _____ ).
∴∠A=∠ECD( __ ).内错角相等,两直线平行平行于同一直线的两条直线互相平行两直线平行,同位角相等 如图,若AB//CD,你能确定∠B、∠D与∠BED 的大小关系吗?说说你的看法. 解:过点E作EF//AB.
∴∠B=∠BEF.
∵AB//CD.
∴∠D =∠DEF.
∴∠B+∠D=∠BEF+∠DEF=∠DEB.
即∠B+∠D=∠DEB. F∴EF//CD.2.如图,AB//CD,探索∠B、∠D与∠DEB的大小关系 .解:过点E作EF//AB.
∴∠B+∠BEF=180°.
∵AB//CD.
∴EF//CD.
∴∠D +∠DEF=180°.
∴∠B+∠D+∠DEB
=∠B+∠D+∠BEF+∠DEF
=360°.
即∠B+∠D+∠DEB=360°. F 【讨论1】如图,AB∥CD,则 :当有一个拐点时: ∠A+∠E+∠C= 360° 当有两个拐点时: ∠A+∠ E1 + ∠ E2 +∠C = 540° 当有三个拐点时: ∠A+∠ E1 + ∠ E2 +∠ E3 +∠C = 720° …若有n个拐点,你能找到规律吗?【讨论2】如图,若AB∥CD, 则:当左边有两个角,右边有一个角时: ∠A+∠C= ∠E当左边有两个角,右边有两个角时: ∠A+∠F= ∠E +∠D当左边有三个角,右边有两个角时: ∠A+∠ F1 +∠C
= ∠ E1 +∠ E2若左边有n个角,右边有m个角;你能找到规律吗?(2019?遵义)如图,∠1+∠2=180°,∠3=104°,则∠4的度数是( )
A.74° B.76°
C.84° D.86°巩固练习B561. 如图所示,AB∥CD∥EF,那么∠BAC+∠ACE+∠CEF= ( )
A. 180° B. 270° C. 360° D. 540° C2.如图所示,在△ABC中,∠B=∠C,∠BAC=80°,AD∥EF,∠1=∠2,求∠BDG的度数. 解:∵AD∥EF,∴∠2=∠DAC.
∵∠1=∠2,∴∠1=∠DAC.
∴GD∥AC.
∵∠BAC=80°,∠B=∠C,
∴2∠C=180°-∠BAC=100°.
∴∠C=50°.
∴∠BDG=50°. ∴∠BDG=∠C.3.已知AB⊥BF,CD⊥BF,∠1= ∠2,
试说明∠3=∠E.∵∠1=∠2∴AB∥EF(内错角相等,两直线平行).(已知),∵AB⊥BF,CD⊥BF,∴AB∥CD∴EF∥CD∴ ∠3= ∠E(垂直于同一条直线的两条直线平行).(平行于同一条直线的两条直线平行). (两直线平行,同位角相等).解: 如图,EF∥AD,∠1=∠2,∠BAC=70 °,
求∠AGD的度数.∵EF∥AD,(已知) ∴∠2=∠3.又∵∠1=∠2,∴∠1=∠3.∴DG∥AB.∴∠BAC+∠AGD=180°.∴∠AGD=180°-∠BAC=180°-70°=110°.(两直线平行,同位角相等)(已知)(等量代换)(内错角相等,两直线平行)(两直线平行,同旁内角互补)解: 如图,AB∥CD,猜想∠A、∠P 、∠PCD的数量关系,并说明理由.ABCDPE解法一:作∠PCE =∠APC,交AB于E.
∴ AP∥CE
∴ ∠A+∠P=∠PCE+∠AEC,
∵AB∥CD ∴ ∠ECD=∠AEC,
∴∠A+∠P =∠PCE+∠ECD=∠PCD.∴ ∠AEC=∠A,∠P=∠PCE. 如图,AB∥CD,猜想∠BAP、∠APC 、∠PCD的数量关系,并说明理由.ABCDPE解法二:作∠APE =∠BAP.
∴ EP∥AB,
∴ EP∥CD,∴∠EPC=∠PCD
∴ ∠APE+∠APC= ∠PCD
即∠BAP+∠APC =∠PCD.∵AB∥CD 判定:已知角的关系得平行的关系.
推平行,用判定.性质:已知平行的关系得角的关系.
知平行,用性质.平行线的“判定”与“性质”有什么不同:课后作业作业
内容教材作业从课后习题中选取自主安排配套练习册练习
5.3.1 平行线的性质人教版 数学 七年级 下册平行线的性质返回【思考】根据同位角相等可以判定两直线平行,反过来如果两直线平行,同位角之间有什么关系呢?内错角、同旁内角之间又有什么关系呢?
1. 掌握平行线的性质,会运用两条直线是平行关系判断角相等或互补.2. 能够根据平行线的性质进行简单的推理.素养目标3. 区分平行线的性质和判定的关系,培养学生逆向思维的能力. 画两条平行线a//b,然后画一条截线c与a、b相交,标出如图所示的角. 度量所形成的8个角的度数,把结果填入下表:【讨论】∠1~ ∠8中,哪些是同位角?它们的度数之间有什么关系?说出你的猜想: 猜想:两条平行线被第三条直线所截,同位角___.
相等abd 再任意画一条截线d,同样度量各个角的度数,你的猜想还成立吗?如果两直线不平行,上述结论还成立吗?一般地,平行线具有如下性质:性质1:两条平行线被第三条直线所截,同位角相等.∴∠1=∠2
(两直线平行,同位角相等)∵a∥b(已知)几何语言:简单说成:两直线平行,同位角相等. 例1 如图,D是AB上一点,E是AC上一点,∠ADE=60°,∠B=60°, ∠AED=40°.(1)DE和BC平行吗?为什么? (2)∠C是多少度?为什么? 答:(1)DE∥BC,
∵∠ADE=60°,∠B=60°,∴∠ADE= ∠B.
∴DE∥BC ( )同位角相等,两直线平行(2) ∠C =40°.
( )
∵∠AED=40°,∴∠C =40°.两直线平行,同位角相等∵DE∥BC ,∴∠C = ∠AED.1. 如图所示,∠1=70°,若m∥n,则∠2= .
2.如图所示,直线m∥n,∠1=70°,∠2=30°,则∠A等于 ( )
A. 30° B. 35°
C. 40° D. 50°70°Cnm21 在上一节中,我们利用“同位角相等,两直线平行”推出了“内错角相等,两直线平行线”,类似地,已知两直线平行,同位角相等,能否得到内错角之间的数量关系? 如图,已知a//b,那么?2与?3相等吗?为什么?解:∵ a∥b(已知),
∴∠1=∠2(两直线平行,同位角相等).
又∵ ∠1=∠3(对顶角相等),
∴ ∠2=∠3(等量代换).性质2:两条平行线被第三条直线所截,内错角相等. ∴∠2=∠3
(两直线平行,内错角相等)∵a∥b(已知)几何语言:简单说成:两直线平行,内错角相等.例2 如图,已知直线a∥b,∠1 = 50°, 求∠2的度数.abc12∴∠ 2= 50° (等量代换)解:∵ a∥b(已知)∴∠ 1= ∠ 2
(两直线平行,内错角相等)又∵∠ 1 = 50° (已知)利用“两直线平行,内错角相等”求角的度数3.如图所示,AC∥BD,∠A=70°,∠C=50°,则
∠1= ,∠2= ,∠3= .70°50°60°如图,已知a//b,那么?2与?4有什么关系呢?为什么?解: ∵a//b (已知), ∴? 1= ? 2(两直线平行,同位角相等).∵ ? 1+ ? 4=180°(邻补角的性质),∴? 2+ ? 4=180°(等量代换).类似地,已知两直线平行,能否得到同旁内角之间的数量关系? 性质3:两条平行线被第三条直线所截,同旁内角互补. ∴∠2+∠4=180 °
(两直线平行,同旁内角互补)∵a∥b(已知)几何语言:简单说成:两直线平行,同旁内角互补. 例3 如图是一块梯形铁片的残余部分,量得∠A=100°,∠B=115°,梯形的另外两个角的度数分别是多少?解:∵梯形上、下底互相平行,
∴ ∠A与∠D互补, ∠B与∠C互补.∴梯形的另外两个角分别是80°、65°.于是∠D=180 °-∠A=180°-100°=80°
∠C= 180 °-∠B=180°-115°=65°4.如图所示,直线a∥b,直线l与a,b分别相交于A、B两点,过点A作直线l的垂线交直线b于点C,若∠1=58°,则∠2的度数为( )
A. 58° B. 42°
C. 32° D. 28°C(2019?日照)如图,将一块三角尺的直角顶点放在直尺的一边上,当∠1=35°时,∠2的度数为( )
A.35° B.45°
C.55° D.65°巩固练习C
1.如图所示,直线a∥b,直线c与直线a,b相交,若∠1=56°,则∠2等于 ( )
A. 24°
B. 34°
C. 56°
D. 124°C2.如图所示,AB∥CD,直线EF与AB,CD分别交于点M,N,过点N的直线GH与AB交于点P,则下列结论错误的是( )
A. ∠EMB=∠END
B. ∠BMN=∠MNC
C. ∠CNH=∠BPG
D. ∠DNG=∠AMED3. 如图所示,直线a∥b,点B在直线a上,AB⊥BC,若
∠1=38°,则∠2的度数为 ( )
A. 38° B. 52° C. 76° D. 142°B4.如图所示,AB∥CD,∠E=40°,∠A=110°,则∠C的度数为( )
A. 60° B. 80° C. 75° D. 70°D5. 如图所示,直线a∥b,Rt△ABC的直角顶点C在直线b上,∠1=20°,则∠2= °. 70解: ∵ AB∥DE( )
∴∠A= ______ ( )
∵AC∥DF( )
∴∠D+ _______=180o ( )
∴∠A+∠D=180o( ) 有这样一道题:如图,若AB∥DE , AC∥DF,试说明∠A+∠D=180o.请补全下面的解答过程,括号内填写依据.已知∠CPD两直线平行,同位角相等已知∠CPD两直线平行,同旁内角互补等量代换 如图,潜望镜中的两面镜子是互相平行放置的,光线经过镜子反射时,∠1=∠2,∠3=∠4,∠2和∠3有什么关系?为什么进入潜望镜的光线和离开潜望镜的光线是平行的?解:∠2=∠3,
∵两直线平行,内错角相等;∴∠2=∠3,∵∠1=∠2,∠3=∠4,
∴∠1=∠2=∠3=∠4,∴ ∠5=∠6,
∴进入潜望镜的光线和离开潜望镜
的光线平行.同位角相等
内错角相等
同旁内角互补两直线平行判定性质平行线的判定与性质的综合应用返回 一辆汽车沿AB方向行驶,在C处拐了一个弯,行驶一段时间到D处又一次改变方向,此时车子与原来的方向是否一致?为什么?2. 进一步熟悉平行线的判定方法和性质.1. 分清平行线的性质和判定;已知平行用性质,要证平行用判定 .素养目标3. 能够综合运用平行线性质和判定进行推理证明.证明:∵ AD ∥BC(已知)
∴ ∠A+∠B=180°( )
∵ ∠AEF=∠B(已知)
∴ ∠A+∠AEF=180°(等量代换)
∴ AD∥EF( )
【思考】在填写依据时要注意什么问题?两直线平行,同旁内角互补同旁内角互补,两直线平行如图,已知:AD∥BC, ∠AEF=∠B,
求证:AD∥EF.1.如图,AB∥EF,∠ECD=∠E,则∠A=∠ECD.
理由如下:
∵∠ECD=∠E,
∴CD∥EF( )
又AB∥EF,
∴CD∥AB( _____ ).
∴∠A=∠ECD( __ ).内错角相等,两直线平行平行于同一直线的两条直线互相平行两直线平行,同位角相等 如图,若AB//CD,你能确定∠B、∠D与∠BED 的大小关系吗?说说你的看法. 解:过点E作EF//AB.
∴∠B=∠BEF.
∵AB//CD.
∴∠D =∠DEF.
∴∠B+∠D=∠BEF+∠DEF=∠DEB.
即∠B+∠D=∠DEB. F∴EF//CD.2.如图,AB//CD,探索∠B、∠D与∠DEB的大小关系 .解:过点E作EF//AB.
∴∠B+∠BEF=180°.
∵AB//CD.
∴EF//CD.
∴∠D +∠DEF=180°.
∴∠B+∠D+∠DEB
=∠B+∠D+∠BEF+∠DEF
=360°.
即∠B+∠D+∠DEB=360°. F 【讨论1】如图,AB∥CD,则 :当有一个拐点时: ∠A+∠E+∠C= 360° 当有两个拐点时: ∠A+∠ E1 + ∠ E2 +∠C = 540° 当有三个拐点时: ∠A+∠ E1 + ∠ E2 +∠ E3 +∠C = 720° …若有n个拐点,你能找到规律吗?【讨论2】如图,若AB∥CD, 则:当左边有两个角,右边有一个角时: ∠A+∠C= ∠E当左边有两个角,右边有两个角时: ∠A+∠F= ∠E +∠D当左边有三个角,右边有两个角时: ∠A+∠ F1 +∠C
= ∠ E1 +∠ E2若左边有n个角,右边有m个角;你能找到规律吗?(2019?遵义)如图,∠1+∠2=180°,∠3=104°,则∠4的度数是( )
A.74° B.76°
C.84° D.86°巩固练习B561. 如图所示,AB∥CD∥EF,那么∠BAC+∠ACE+∠CEF= ( )
A. 180° B. 270° C. 360° D. 540° C2.如图所示,在△ABC中,∠B=∠C,∠BAC=80°,AD∥EF,∠1=∠2,求∠BDG的度数. 解:∵AD∥EF,∴∠2=∠DAC.
∵∠1=∠2,∴∠1=∠DAC.
∴GD∥AC.
∵∠BAC=80°,∠B=∠C,
∴2∠C=180°-∠BAC=100°.
∴∠C=50°.
∴∠BDG=50°. ∴∠BDG=∠C.3.已知AB⊥BF,CD⊥BF,∠1= ∠2,
试说明∠3=∠E.∵∠1=∠2∴AB∥EF(内错角相等,两直线平行).(已知),∵AB⊥BF,CD⊥BF,∴AB∥CD∴EF∥CD∴ ∠3= ∠E(垂直于同一条直线的两条直线平行).(平行于同一条直线的两条直线平行). (两直线平行,同位角相等).解: 如图,EF∥AD,∠1=∠2,∠BAC=70 °,
求∠AGD的度数.∵EF∥AD,(已知) ∴∠2=∠3.又∵∠1=∠2,∴∠1=∠3.∴DG∥AB.∴∠BAC+∠AGD=180°.∴∠AGD=180°-∠BAC=180°-70°=110°.(两直线平行,同位角相等)(已知)(等量代换)(内错角相等,两直线平行)(两直线平行,同旁内角互补)解: 如图,AB∥CD,猜想∠A、∠P 、∠PCD的数量关系,并说明理由.ABCDPE解法一:作∠PCE =∠APC,交AB于E.
∴ AP∥CE
∴ ∠A+∠P=∠PCE+∠AEC,
∵AB∥CD ∴ ∠ECD=∠AEC,
∴∠A+∠P =∠PCE+∠ECD=∠PCD.∴ ∠AEC=∠A,∠P=∠PCE. 如图,AB∥CD,猜想∠BAP、∠APC 、∠PCD的数量关系,并说明理由.ABCDPE解法二:作∠APE =∠BAP.
∴ EP∥AB,
∴ EP∥CD,∴∠EPC=∠PCD
∴ ∠APE+∠APC= ∠PCD
即∠BAP+∠APC =∠PCD.∵AB∥CD 判定:已知角的关系得平行的关系.
推平行,用判定.性质:已知平行的关系得角的关系.
知平行,用性质.平行线的“判定”与“性质”有什么不同:课后作业作业
内容教材作业从课后习题中选取自主安排配套练习册练习
