人教版七年级上册数学:3.4实际问题与一元一次方程---方案选择问题 课件(16张ppt)
文档属性
| 名称 | 人教版七年级上册数学:3.4实际问题与一元一次方程---方案选择问题 课件(16张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 180.7KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-27 08:13:17 | ||
图片预览




文档简介
(共16张PPT)
3.4.5 实际问题与一元一次方程
---方案选择问题
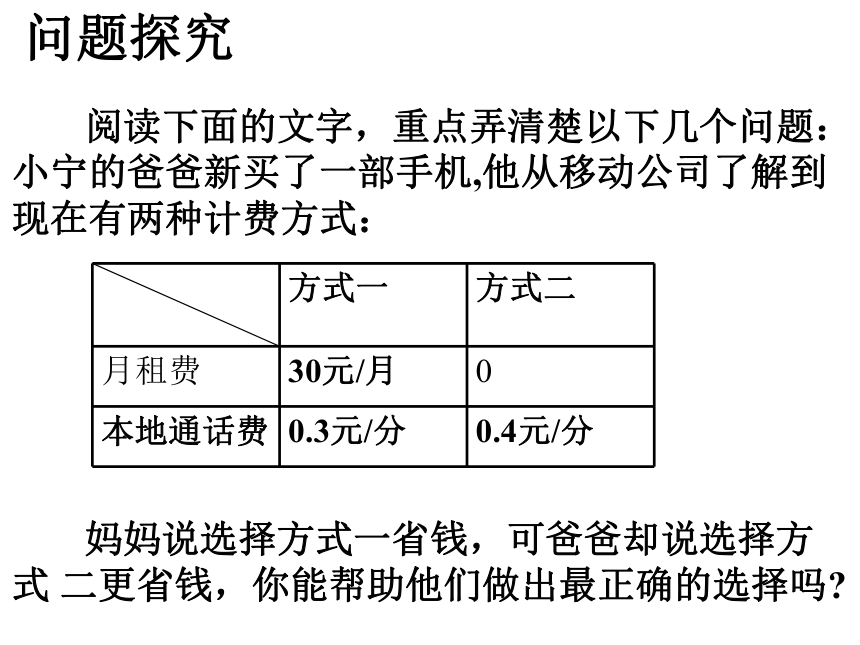
为响应国家提速降费号召,近日中国电信、中国移动和中国联通相对以往的套餐确实作出了改变,相继降低资费。作为消费者,我们该如何选择呢?
情境导入
阅读下面的文字,重点弄清楚以下几个问题:小宁的爸爸新买了一部手机,他从移动公司了解到现在有两种计费方式:
妈妈说选择方式一省钱,可爸爸却说选择方式 二更省钱,你能帮助他们做出最正确的选择吗?
方式一 方式二
月租费 30元/月 0
本地通话费 0.3元/分 0.4元/分
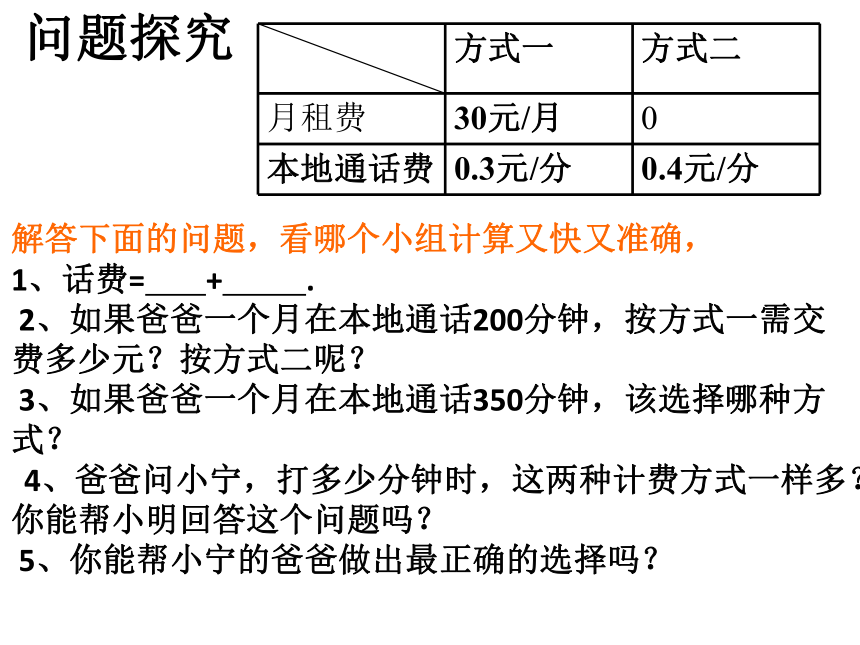
问题探究
解答下面的问题,看哪个小组计算又快又准确,
1、话费= + .
2、如果爸爸一个月在本地通话200分钟,按方式一需交费多少元?按方式二呢?
3、如果爸爸一个月在本地通话350分钟,该选择哪种方式?
4、爸爸问小宁,打多少分钟时,这两种计费方式一样多?你能帮小明回答这个问题吗?
5、你能帮小宁的爸爸做出最正确的选择吗?
问题探究
方式一 方式二
月租费 30元/月 0
本地通话费 0.3元/分 0.4元/分
1、话费= 月租费+本地通话费.
2、如果爸爸一个月在本地通话200分钟,按方式一需交费多少元?按方式二呢?
解:方式一:30+0.3×200=90(元)
方式二:0.4×200=80(元)
所以选方式二.
解:方式一:30+0.3×350=135(元)
方式二:0.4×350=140(元)
所以选方式一.
3、如果爸爸一个月在本地通话350分钟,该选择哪种方式?
问题探究
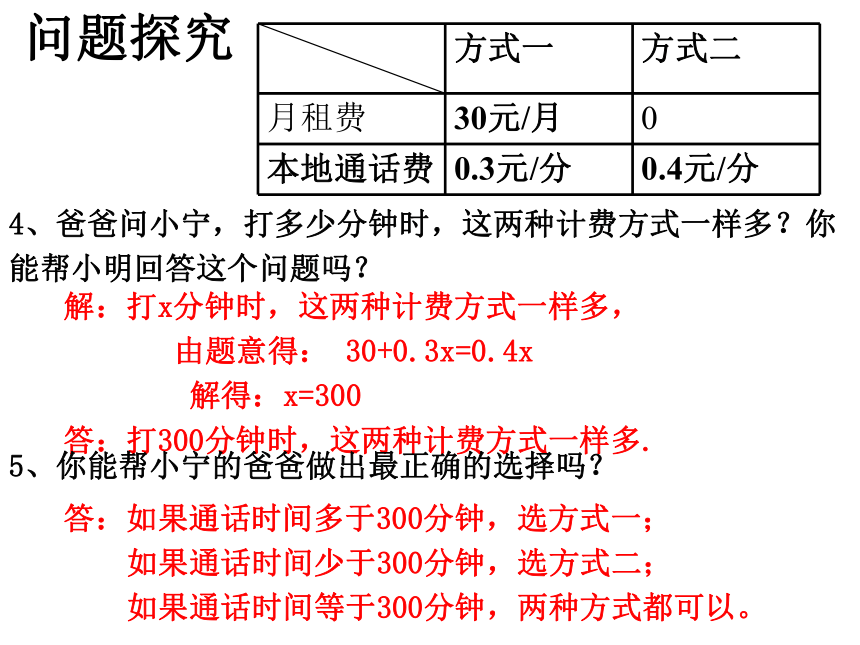
4、爸爸问小宁,打多少分钟时,这两种计费方式一样多?你能帮小明回答这个问题吗?
解:打x分钟时,这两种计费方式一样多,
由题意得: 30+0.3x=0.4x
解得:x=300
答:打300分钟时,这两种计费方式一样多.
5、你能帮小宁的爸爸做出最正确的选择吗?
答:如果通话时间多于300分钟,选方式一;
如果通话时间少于300分钟,选方式二;
如果通话时间等于300分钟,两种方式都可以。
问题探究
方式一 方式二
月租费 30元/月 0
本地通话费 0.3元/分 0.4元/分
例题:唐人书店出售一种购书会员卡,每张会员卡20元,仅限本人使用,有效期一年,凭卡购书可享受8折优惠,无卡购书不打折。请讨论:
(1)购书多少元时,买卡与不买卡花钱一样多?
(2)什么情况下买卡划算?
(3)什么情况下,不买卡划算?
(4)小康持会员卡购书,一年共节省80元,请你帮他计算一下这一年他在唐人书店买书共花了多少钱?
例题解析
(1)购书多少元时,买卡与不买卡花钱一样多?
解:设购书x元时,买卡与不买卡花钱一样多,
由题意得: 20+0.8x=x
解得:x=100
答:购书100元时,买卡与不买卡花钱一样多.
(2)什么情况下买卡划算?
(3)什么情况下,不买卡划算?
例题:唐人书店出售一种购书会员卡,每张会员卡20元,仅限本人使用,有效期一年,凭卡购书可享受8折优惠,无卡购书不打折。请讨论:
(4)小康持会员卡购书,一年共节省80元,请你帮他计算一下这一年他在唐人书店买书共花了多少钱?
解:设他在唐人书店买书花了x元钱,
由题意得: 20+0.8x=x-80
解得:x=500
答:他在唐人书店买书花了500元钱.
校长带领“三好学生”去旅行,已知甲、乙两家旅行社的全票价均为240元,为了争取游客,甲旅行社推出的优惠方案是:校长全票,其余学生享受半价优惠;乙旅行社:包括校长在内,全部按票价的6折优惠。
(1)当学生人数为多少时,两旅行社收费一样?
(2)请根据实际人数为校长设计一个省钱的旅行方案。
拓展提高
(1)当学生人数为多少时,两旅行社收费一样?
解:设学生人数为x人时,两家旅行社收费一样,
由题意得:240+0.5×240x=0.6×240(x+1)
解得: x=4
答:当学生人数为4人时,两家旅行社收费一样.
(2)请根据实际人数为校长设计一个省钱的旅行方案。
答:当学生人数多于4人时,选甲旅行社省钱;
当学生人数少于4人时,选乙旅行社省钱;
当学生人数等于4人时,两家旅行社花费一样.
校长带领“三好学生”去旅行,已知甲、乙两家旅行社的全票价均为240元,为了争取游客,甲旅行社推出的优惠方案是:校长全票,其余学生享受半价优惠;乙旅行社:包括校长在内,全部按票价的6折优惠。
2、为了积极配合学校开展的“阳光体育”活动,七(1)班同学准备购买一些乒乓球和乒乓球拍,每副球拍30元,每盒乒乓球5元,甲、乙两商店又推出不同的优惠方案:甲商店买一副球拍赠送1盒乒乓球;乙商店全部按定价的9折优惠。同学们需要球拍5副,乒乓球若干盒(不小于5盒),问:
(1)当购买乒乓球多少盒时,到两家商店花钱一样多?
(2)若同学们需要15盒乒乓球,请你去办这件事,你决定去哪家商店购买?
跟踪训练
(1)当购买乒乓球多少盒时,到两家商店花钱一样多?
解:设当购买乒乓球x盒时,到两家商店花钱一样多,
由题意得:(5×30+5x)×0.9=5×30+5(x-5)
解得: x=20
答:当购买乒乓球20盒时,到两家商店花钱一样多.
(2)若同学们需要15盒乒乓球,请你去办这件事,你决定去哪家商店购买?
解:甲商店花钱:(5×30+5×15)×0.9=202.5(元)
乙商店花钱:5×30+5×(15-5)=200(元)
答:当购买乒乓球15盒时,选乙商店省钱.
2、为了积极配合学校开展的“阳光体育”活动,七(1)班同学准备购买一些乒乓球和乒乓球拍,每副球拍30元,每盒乒乓球5元,甲、乙两商店又推出不同的优惠方案:甲商店买一副球拍赠送1盒乒乓球;乙商店全部按定价的9折优惠。同学们需要球拍5副,乒乓球若干盒(不小于5盒)
课堂小结
1.谈谈你今天又学到了那些知识?
2.对照学习目标,检查自己哪些知识已经掌握了,哪些知识还有疑惑?
1.商场计划拨款9万元,从厂家购进50台电视机,已知该厂家生产三种不同型号的电视机,出厂价分别为:甲种每台1500元,乙种每台2100元,丙种每台2500元。
(1)若商场同时购进两种不同型号的电视机共50台,用去9万元,请你研究一下商场的进货方案。
(2)若商场销售一台甲种电视机可获利150元,销一台乙种电视机可获利200元,销售一台丙种电视机获利250元,那么你会选择哪种进货方案?
当堂达标
(1)方案一:进甲种电视机χ台,乙种(50-χ)台,
则1500χ+(50-χ)×2100=90000
χ=25,50-χ=25
故甲、乙两种电视机各进25台。
方案二:进甲种电视机у台,丙种(50-у)台,
则1500у+(50-у)×2500=90000,
у=35,50-у=15
故甲种进35台,丙种15台。
方案三:进乙种电视机z台丙种(50-z)台。
则2100z+(150-z)×2500=90000,
Z=87.5(舍去)
因此有两种进货方案。
(2)获利情况:
方案一:150×25+200×15=8750(元)
方案二:35×150+15×250=9000(元)
因为:8750<90000,
所以应选择方案二进货。
3.4.5 实际问题与一元一次方程
---方案选择问题
为响应国家提速降费号召,近日中国电信、中国移动和中国联通相对以往的套餐确实作出了改变,相继降低资费。作为消费者,我们该如何选择呢?
情境导入
阅读下面的文字,重点弄清楚以下几个问题:小宁的爸爸新买了一部手机,他从移动公司了解到现在有两种计费方式:
妈妈说选择方式一省钱,可爸爸却说选择方式 二更省钱,你能帮助他们做出最正确的选择吗?
方式一 方式二
月租费 30元/月 0
本地通话费 0.3元/分 0.4元/分
问题探究
解答下面的问题,看哪个小组计算又快又准确,
1、话费= + .
2、如果爸爸一个月在本地通话200分钟,按方式一需交费多少元?按方式二呢?
3、如果爸爸一个月在本地通话350分钟,该选择哪种方式?
4、爸爸问小宁,打多少分钟时,这两种计费方式一样多?你能帮小明回答这个问题吗?
5、你能帮小宁的爸爸做出最正确的选择吗?
问题探究
方式一 方式二
月租费 30元/月 0
本地通话费 0.3元/分 0.4元/分
1、话费= 月租费+本地通话费.
2、如果爸爸一个月在本地通话200分钟,按方式一需交费多少元?按方式二呢?
解:方式一:30+0.3×200=90(元)
方式二:0.4×200=80(元)
所以选方式二.
解:方式一:30+0.3×350=135(元)
方式二:0.4×350=140(元)
所以选方式一.
3、如果爸爸一个月在本地通话350分钟,该选择哪种方式?
问题探究
4、爸爸问小宁,打多少分钟时,这两种计费方式一样多?你能帮小明回答这个问题吗?
解:打x分钟时,这两种计费方式一样多,
由题意得: 30+0.3x=0.4x
解得:x=300
答:打300分钟时,这两种计费方式一样多.
5、你能帮小宁的爸爸做出最正确的选择吗?
答:如果通话时间多于300分钟,选方式一;
如果通话时间少于300分钟,选方式二;
如果通话时间等于300分钟,两种方式都可以。
问题探究
方式一 方式二
月租费 30元/月 0
本地通话费 0.3元/分 0.4元/分
例题:唐人书店出售一种购书会员卡,每张会员卡20元,仅限本人使用,有效期一年,凭卡购书可享受8折优惠,无卡购书不打折。请讨论:
(1)购书多少元时,买卡与不买卡花钱一样多?
(2)什么情况下买卡划算?
(3)什么情况下,不买卡划算?
(4)小康持会员卡购书,一年共节省80元,请你帮他计算一下这一年他在唐人书店买书共花了多少钱?
例题解析
(1)购书多少元时,买卡与不买卡花钱一样多?
解:设购书x元时,买卡与不买卡花钱一样多,
由题意得: 20+0.8x=x
解得:x=100
答:购书100元时,买卡与不买卡花钱一样多.
(2)什么情况下买卡划算?
(3)什么情况下,不买卡划算?
例题:唐人书店出售一种购书会员卡,每张会员卡20元,仅限本人使用,有效期一年,凭卡购书可享受8折优惠,无卡购书不打折。请讨论:
(4)小康持会员卡购书,一年共节省80元,请你帮他计算一下这一年他在唐人书店买书共花了多少钱?
解:设他在唐人书店买书花了x元钱,
由题意得: 20+0.8x=x-80
解得:x=500
答:他在唐人书店买书花了500元钱.
校长带领“三好学生”去旅行,已知甲、乙两家旅行社的全票价均为240元,为了争取游客,甲旅行社推出的优惠方案是:校长全票,其余学生享受半价优惠;乙旅行社:包括校长在内,全部按票价的6折优惠。
(1)当学生人数为多少时,两旅行社收费一样?
(2)请根据实际人数为校长设计一个省钱的旅行方案。
拓展提高
(1)当学生人数为多少时,两旅行社收费一样?
解:设学生人数为x人时,两家旅行社收费一样,
由题意得:240+0.5×240x=0.6×240(x+1)
解得: x=4
答:当学生人数为4人时,两家旅行社收费一样.
(2)请根据实际人数为校长设计一个省钱的旅行方案。
答:当学生人数多于4人时,选甲旅行社省钱;
当学生人数少于4人时,选乙旅行社省钱;
当学生人数等于4人时,两家旅行社花费一样.
校长带领“三好学生”去旅行,已知甲、乙两家旅行社的全票价均为240元,为了争取游客,甲旅行社推出的优惠方案是:校长全票,其余学生享受半价优惠;乙旅行社:包括校长在内,全部按票价的6折优惠。
2、为了积极配合学校开展的“阳光体育”活动,七(1)班同学准备购买一些乒乓球和乒乓球拍,每副球拍30元,每盒乒乓球5元,甲、乙两商店又推出不同的优惠方案:甲商店买一副球拍赠送1盒乒乓球;乙商店全部按定价的9折优惠。同学们需要球拍5副,乒乓球若干盒(不小于5盒),问:
(1)当购买乒乓球多少盒时,到两家商店花钱一样多?
(2)若同学们需要15盒乒乓球,请你去办这件事,你决定去哪家商店购买?
跟踪训练
(1)当购买乒乓球多少盒时,到两家商店花钱一样多?
解:设当购买乒乓球x盒时,到两家商店花钱一样多,
由题意得:(5×30+5x)×0.9=5×30+5(x-5)
解得: x=20
答:当购买乒乓球20盒时,到两家商店花钱一样多.
(2)若同学们需要15盒乒乓球,请你去办这件事,你决定去哪家商店购买?
解:甲商店花钱:(5×30+5×15)×0.9=202.5(元)
乙商店花钱:5×30+5×(15-5)=200(元)
答:当购买乒乓球15盒时,选乙商店省钱.
2、为了积极配合学校开展的“阳光体育”活动,七(1)班同学准备购买一些乒乓球和乒乓球拍,每副球拍30元,每盒乒乓球5元,甲、乙两商店又推出不同的优惠方案:甲商店买一副球拍赠送1盒乒乓球;乙商店全部按定价的9折优惠。同学们需要球拍5副,乒乓球若干盒(不小于5盒)
课堂小结
1.谈谈你今天又学到了那些知识?
2.对照学习目标,检查自己哪些知识已经掌握了,哪些知识还有疑惑?
1.商场计划拨款9万元,从厂家购进50台电视机,已知该厂家生产三种不同型号的电视机,出厂价分别为:甲种每台1500元,乙种每台2100元,丙种每台2500元。
(1)若商场同时购进两种不同型号的电视机共50台,用去9万元,请你研究一下商场的进货方案。
(2)若商场销售一台甲种电视机可获利150元,销一台乙种电视机可获利200元,销售一台丙种电视机获利250元,那么你会选择哪种进货方案?
当堂达标
(1)方案一:进甲种电视机χ台,乙种(50-χ)台,
则1500χ+(50-χ)×2100=90000
χ=25,50-χ=25
故甲、乙两种电视机各进25台。
方案二:进甲种电视机у台,丙种(50-у)台,
则1500у+(50-у)×2500=90000,
у=35,50-у=15
故甲种进35台,丙种15台。
方案三:进乙种电视机z台丙种(50-z)台。
则2100z+(150-z)×2500=90000,
Z=87.5(舍去)
因此有两种进货方案。
(2)获利情况:
方案一:150×25+200×15=8750(元)
方案二:35×150+15×250=9000(元)
因为:8750<90000,
所以应选择方案二进货。
