5.3.1 应用一元一次方程——水箱变高了课件
文档属性
| 名称 | 5.3.1 应用一元一次方程——水箱变高了课件 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-28 00:00:00 | ||
图片预览





文档简介
(共26张PPT)
北师大版
七年级上
3 应用一元一次方程——水箱变高了
第1课时 列方程解实际问题的一般
方法
回忆
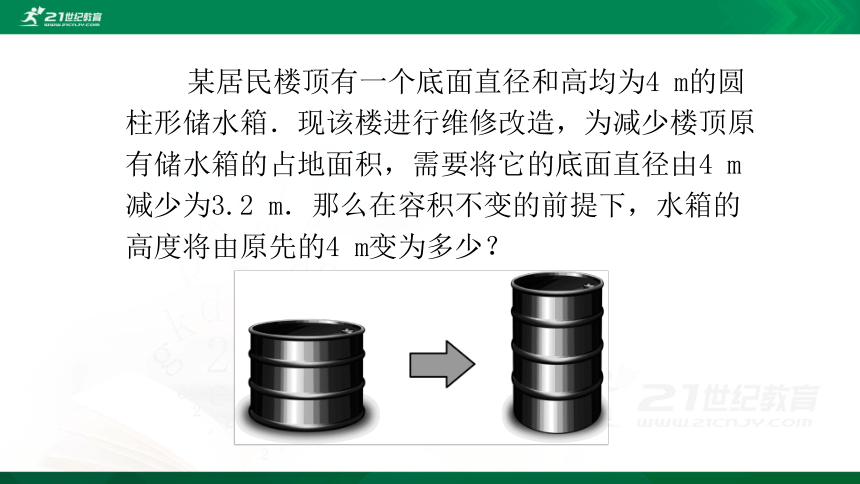
某居民楼顶有一个底面直径和高均为4 m的圆柱形储水箱.现该楼进行维修改造,为减少楼顶原有储水箱的占地面积,需要将它的底面直径由4 m减少为3.2 m.那么在容积不变的前提下,水箱的高度将由原先的4 m变为多少?
1、等积问题
①前后容积(体积)相等
②前后面积相等
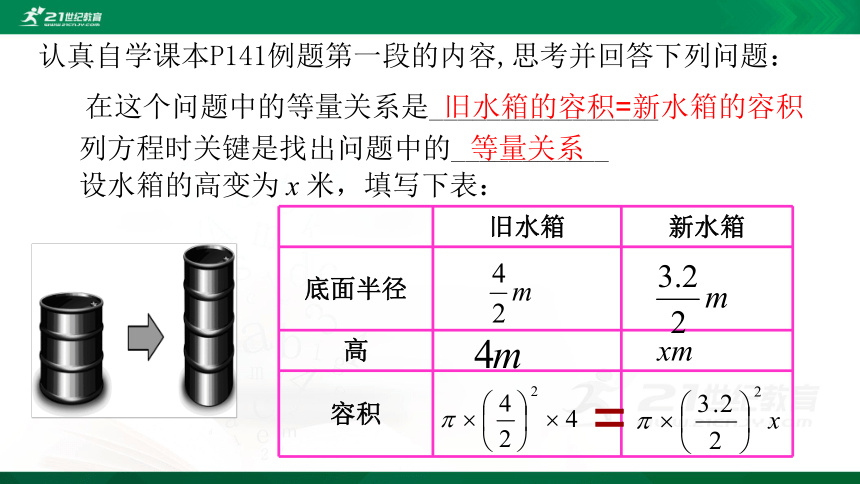
认真自学课本P141例题第一段的内容,思考并回答下列问题:
在这个问题中的等量关系是________________
设水箱的高变为 x 米,填写下表:
旧水箱 新水箱
底面半径
高
容积
=
旧水箱的容积=新水箱的容积
列方程时关键是找出问题中的___________
等量关系
解:设水箱的高变为 x米,
解得
答:高变成了 6.25 米。
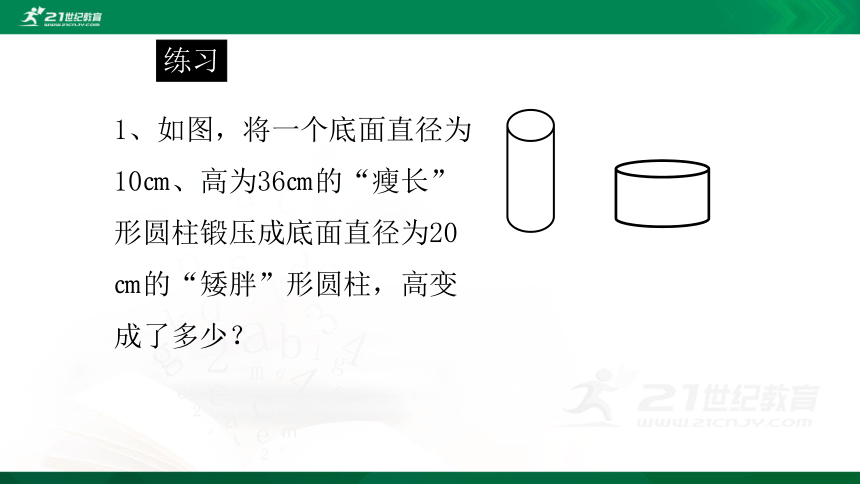
1、如图,将一个底面直径为10㎝、高为36㎝的“瘦长”形圆柱锻压成底面直径为20㎝的“矮胖”形圆柱,高变成了多少?
练习
1、分析:这个问题中的等量关系:
锻压前的体积=锻压后的体积
解:设锻压后圆柱的高为 ㎝,填写下表:
锻压前 锻压后
底面半径 5㎝ 10㎝
高 36㎝ ㎝
体积
∴根据相等关系,列出方程:
答:高变成了9㎝.
2、有一个底面半径是5厘米的圆柱形容器,油液中浸有钢球5颗,若从中捞出钢球,液面由25厘米下降到18厘米,问每颗钢珠的体积是 立方厘米
分析:
油液的变化体积=钢珠的体积
油液的高度下降了:25-18=7cm
答:每颗钢珠的体积是 立方厘米
解:设每颗钢珠的体积为x立方厘米
合作探究
(1)若该长方形的长比宽多1.4m,此时长方形的长、宽各是多少?
用一根长为10m的铁丝围成一个长方形.
长方形的周长(或长与宽的和)不变
在这个过程中什么没有发生变化?
2、图形的等长变化
前后的周长相等
x m
(x+1.4) m
等量关系:
(长+宽)× 2=周长
解: 设此时长方形的宽为xm,则它的长为(x+1.4)m. 根据题意,得
(x+1.4 +x) ×2 =10
解得 x =1.8
1.8+1.4=3.2
此时长方形的长为3.2m,宽为1.8m.
(2)若该长方形的长比宽多0.8m,此时长方形的长和宽各为多少米?它围成的长方形与(1)中所围成的长方形相比,面积有什么变化?
x m
(x+0.8) m
用一根长为10m的铁丝围成一个长方形.
解:设此时长方形的宽为xm,则它的长为(x+0.8)m.根据题意,得
(x+0.8 +x) ×2 =10
解得 x=2.1
2.1+0.8=2.9
此时长方形的长为2.9m,宽为2.1m,面积为2.9 ×2.1=6.09(m2),(1)中长方形的面积为3.2 × 1.8=5.76(m2).
此时长方形的面积比(1)中长方形的面积增大6.09-5.76=0.33(m2).
x m
(x+0.8) m
(3)若该长方形的长与宽相等,即围成一个正方形,那么正方形的边长是多少?它围成的正方形的面积与(2)中相比,又有什么变化?
x m
(x +x) ×2 =10
解得 x=2.5
正方形的面积为2.5 × 2.5 =6. 25(m2)
解:设正方形的边长为xm.
根据题意,得
比(2)中面积增大 6. 25 -6.09=0.16(m2)
正方形的边长为2.5m
面积:1.8 × 3.2=5.76
面积:
2.9 ×2.1=6.09
面积:
2.5 × 2.5 =6. 25
围成正方形时面积最大
比较
例1 用两根等长的铁丝分别绕成一个正方形和一个圆,已知正方形的边长比圆的半径长2(π-2) m,求这两根等长的铁丝的长度,并通过计算说明谁的面积大.
典例精析
[解析] 比较两图形的面积大小,关键是通过题中的等量关系列方程求得圆的半径和正方形的边长,本题的等量关系为正方形的周长=圆的周长.
解:设圆的半径为r m,则正方形的边长为[r+2(π-2)]m.根据题意,得
答:铁丝的长为8π m,圆的面积较大.
因为4π×4>4π×π,所以16π>4π2,所以圆的面积大.
正方形的面积为[4+2(π-2)]2=4π2(m 2).
所以圆的面积是π×42=16π(m 2),
所以铁丝的长为2πr=8π(m).
2πr=4(r+2π-4),解得r=4.
周长固定;围成图形时,圆的面积最大,正方形面积次之
例2 一种牙膏出口处直径为5 mm,小明每次刷牙都挤出1 cm长的牙膏,这样一支牙膏可以用36次,该品牌牙膏推出新包装,只是将出口处直径改为6 mm,小明还是按习惯每次挤出1 cm的牙膏,这样,这一支牙膏能用多少次?
解:设这一支牙膏能用x次,根据题意得
π×2.52×10×36=π×32×10x.
解这个方程,得x=25.
答:这一支牙膏能用25次.
2.墙上钉着用一根彩绳围成的梯形形状的饰物,如图实线所示(单位:cm).小颖将梯形下底的钉子去掉,并将这根彩绳钉成一个长方形,如图虚线所示.小颖所钉长方形的长、宽各为多少厘米?如果设长方形的长为x cm,根据题意,可列方程为( )
A.2(x+10)=10×4+6×2
B.2(x+10)=10×3+6×2
C.2x+10=10×4+6×2
D.2(x+10)=10×2+6×2
A
4.如图,小明从一个正方形的纸片上剪下一个宽为6 cm的长条后,再从剩下的纸片上剪下一个宽为8 cm的长条.如果两次剪下的长条面积正好相等,那么原正方形的边长是( )
A.20 cm B.24 cm
C.48 cm D.144 cm
B
5.如图,一个装有半瓶多饮料的饮料瓶中,饮料的高度为20 cm;把饮料瓶倒过来放置,饮料瓶空余部分的高度为5 cm.已知饮料瓶的容积为30 cm3,则瓶内现有饮料________cm3.
24
你认为列一元一次方程解应用题的主要步骤有哪些?关键是什么?
1.审——通过审题找出等量关系.
6.答——注意单位名称.
5.检——检验求出的值是否为方程的解,并检验是否符合
实际问题.
4.解——求出方程的解(对间接设的未知数切忌继续求解).
3.列——依据找到的等量关系,列出方程.
2.设——设出合理的未知数(直接或间接),注意单位名称.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
北师大版
七年级上
3 应用一元一次方程——水箱变高了
第1课时 列方程解实际问题的一般
方法
回忆
某居民楼顶有一个底面直径和高均为4 m的圆柱形储水箱.现该楼进行维修改造,为减少楼顶原有储水箱的占地面积,需要将它的底面直径由4 m减少为3.2 m.那么在容积不变的前提下,水箱的高度将由原先的4 m变为多少?
1、等积问题
①前后容积(体积)相等
②前后面积相等
认真自学课本P141例题第一段的内容,思考并回答下列问题:
在这个问题中的等量关系是________________
设水箱的高变为 x 米,填写下表:
旧水箱 新水箱
底面半径
高
容积
=
旧水箱的容积=新水箱的容积
列方程时关键是找出问题中的___________
等量关系
解:设水箱的高变为 x米,
解得
答:高变成了 6.25 米。
1、如图,将一个底面直径为10㎝、高为36㎝的“瘦长”形圆柱锻压成底面直径为20㎝的“矮胖”形圆柱,高变成了多少?
练习
1、分析:这个问题中的等量关系:
锻压前的体积=锻压后的体积
解:设锻压后圆柱的高为 ㎝,填写下表:
锻压前 锻压后
底面半径 5㎝ 10㎝
高 36㎝ ㎝
体积
∴根据相等关系,列出方程:
答:高变成了9㎝.
2、有一个底面半径是5厘米的圆柱形容器,油液中浸有钢球5颗,若从中捞出钢球,液面由25厘米下降到18厘米,问每颗钢珠的体积是 立方厘米
分析:
油液的变化体积=钢珠的体积
油液的高度下降了:25-18=7cm
答:每颗钢珠的体积是 立方厘米
解:设每颗钢珠的体积为x立方厘米
合作探究
(1)若该长方形的长比宽多1.4m,此时长方形的长、宽各是多少?
用一根长为10m的铁丝围成一个长方形.
长方形的周长(或长与宽的和)不变
在这个过程中什么没有发生变化?
2、图形的等长变化
前后的周长相等
x m
(x+1.4) m
等量关系:
(长+宽)× 2=周长
解: 设此时长方形的宽为xm,则它的长为(x+1.4)m. 根据题意,得
(x+1.4 +x) ×2 =10
解得 x =1.8
1.8+1.4=3.2
此时长方形的长为3.2m,宽为1.8m.
(2)若该长方形的长比宽多0.8m,此时长方形的长和宽各为多少米?它围成的长方形与(1)中所围成的长方形相比,面积有什么变化?
x m
(x+0.8) m
用一根长为10m的铁丝围成一个长方形.
解:设此时长方形的宽为xm,则它的长为(x+0.8)m.根据题意,得
(x+0.8 +x) ×2 =10
解得 x=2.1
2.1+0.8=2.9
此时长方形的长为2.9m,宽为2.1m,面积为2.9 ×2.1=6.09(m2),(1)中长方形的面积为3.2 × 1.8=5.76(m2).
此时长方形的面积比(1)中长方形的面积增大6.09-5.76=0.33(m2).
x m
(x+0.8) m
(3)若该长方形的长与宽相等,即围成一个正方形,那么正方形的边长是多少?它围成的正方形的面积与(2)中相比,又有什么变化?
x m
(x +x) ×2 =10
解得 x=2.5
正方形的面积为2.5 × 2.5 =6. 25(m2)
解:设正方形的边长为xm.
根据题意,得
比(2)中面积增大 6. 25 -6.09=0.16(m2)
正方形的边长为2.5m
面积:1.8 × 3.2=5.76
面积:
2.9 ×2.1=6.09
面积:
2.5 × 2.5 =6. 25
围成正方形时面积最大
比较
例1 用两根等长的铁丝分别绕成一个正方形和一个圆,已知正方形的边长比圆的半径长2(π-2) m,求这两根等长的铁丝的长度,并通过计算说明谁的面积大.
典例精析
[解析] 比较两图形的面积大小,关键是通过题中的等量关系列方程求得圆的半径和正方形的边长,本题的等量关系为正方形的周长=圆的周长.
解:设圆的半径为r m,则正方形的边长为[r+2(π-2)]m.根据题意,得
答:铁丝的长为8π m,圆的面积较大.
因为4π×4>4π×π,所以16π>4π2,所以圆的面积大.
正方形的面积为[4+2(π-2)]2=4π2(m 2).
所以圆的面积是π×42=16π(m 2),
所以铁丝的长为2πr=8π(m).
2πr=4(r+2π-4),解得r=4.
周长固定;围成图形时,圆的面积最大,正方形面积次之
例2 一种牙膏出口处直径为5 mm,小明每次刷牙都挤出1 cm长的牙膏,这样一支牙膏可以用36次,该品牌牙膏推出新包装,只是将出口处直径改为6 mm,小明还是按习惯每次挤出1 cm的牙膏,这样,这一支牙膏能用多少次?
解:设这一支牙膏能用x次,根据题意得
π×2.52×10×36=π×32×10x.
解这个方程,得x=25.
答:这一支牙膏能用25次.
2.墙上钉着用一根彩绳围成的梯形形状的饰物,如图实线所示(单位:cm).小颖将梯形下底的钉子去掉,并将这根彩绳钉成一个长方形,如图虚线所示.小颖所钉长方形的长、宽各为多少厘米?如果设长方形的长为x cm,根据题意,可列方程为( )
A.2(x+10)=10×4+6×2
B.2(x+10)=10×3+6×2
C.2x+10=10×4+6×2
D.2(x+10)=10×2+6×2
A
4.如图,小明从一个正方形的纸片上剪下一个宽为6 cm的长条后,再从剩下的纸片上剪下一个宽为8 cm的长条.如果两次剪下的长条面积正好相等,那么原正方形的边长是( )
A.20 cm B.24 cm
C.48 cm D.144 cm
B
5.如图,一个装有半瓶多饮料的饮料瓶中,饮料的高度为20 cm;把饮料瓶倒过来放置,饮料瓶空余部分的高度为5 cm.已知饮料瓶的容积为30 cm3,则瓶内现有饮料________cm3.
24
你认为列一元一次方程解应用题的主要步骤有哪些?关键是什么?
1.审——通过审题找出等量关系.
6.答——注意单位名称.
5.检——检验求出的值是否为方程的解,并检验是否符合
实际问题.
4.解——求出方程的解(对间接设的未知数切忌继续求解).
3.列——依据找到的等量关系,列出方程.
2.设——设出合理的未知数(直接或间接),注意单位名称.
谢谢
21世纪教育网(www.21cnjy.com) 中小学教育资源网站
有大把高质量资料?一线教师?一线教研员?
欢迎加入21世纪教育网教师合作团队!!月薪过万不是梦!!
详情请看:
https://www.21cnjy.com/help/help_extract.php
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
