青岛版九年级数学下册第5章 对函数的再探索5.6 二次函数与一元二次方程课件(共28张)
文档属性
| 名称 | 青岛版九年级数学下册第5章 对函数的再探索5.6 二次函数与一元二次方程课件(共28张) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 青岛版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-29 00:00:00 | ||
图片预览






文档简介
(共28张PPT)
5.6. 二次函数的图像与一元二次方程
1、 一元二次方程ax2+bx+c=0(a≠0)的根的判别式△ = 。
方程根的情况是:当△﹥0 时方程 ;
当△=0时,方程 ;
当△﹤0时,方程 。
b2-4ac
有两个不等实数根
有两个相等实数根
没有实数根
2 、 二次函数y=ax2+bx+c(a、b、c是常数,且a≠0)图像
是一条 ,
复习提问
抛物线
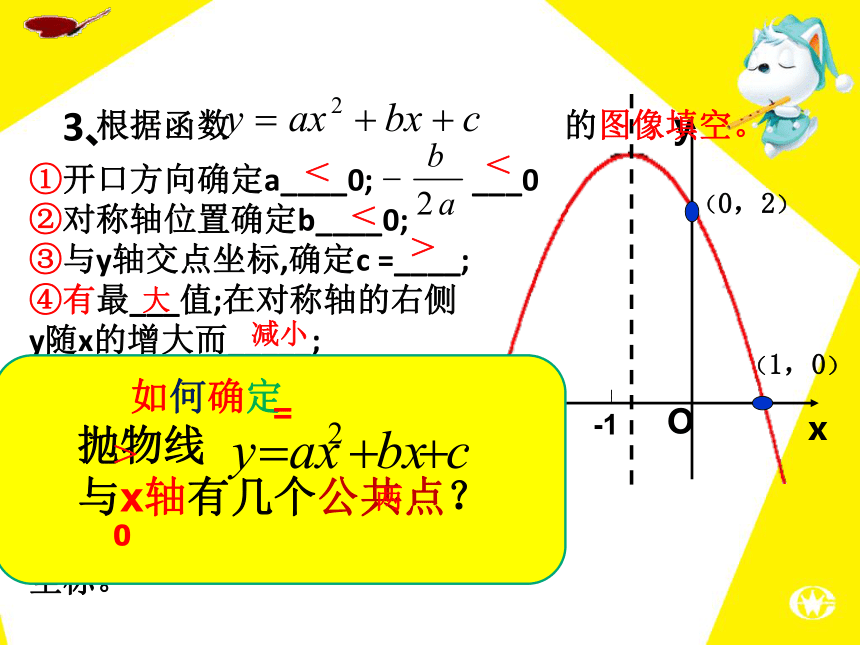
3、
(0,2)
(1,0)
x
y
O
根据函数 的图像填空。
①开口方向确定a____0; ___0
②对称轴位置确定b____0;
③与y轴交点坐标,确定c =____;
④有最___值;在对称轴的右侧
y随x的增大而_____;
⑤特殊的值所得到的特殊的式子:
当x=1时,a+b+c___0,当x=-1时,
a-b+c___0 .
⑥与x轴公共点个数为____个。
当y=____时,可求出公共点的
坐标。
-1
如何确定
抛物线
与x轴有几个公共点?
<
<
<
>
减小
大
=
>
两
0
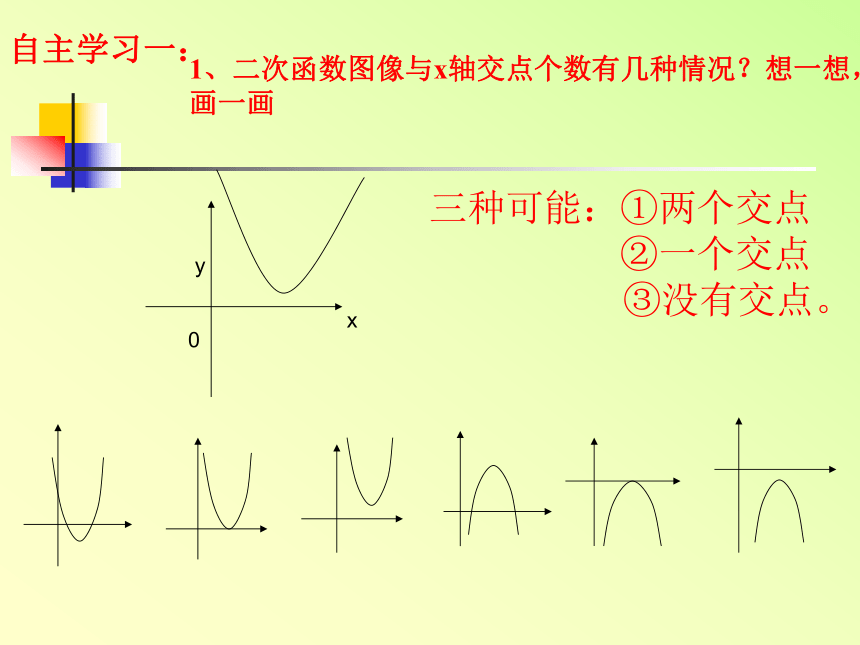
1、二次函数图像与x轴交点个数有几种情况?想一想,
画一画
y
0
三种可能:①两个交点
②一个交点
③没有交点。
自主学习一:
(1). 图象y=x2+2x与x轴交点个数( )
一元二次方程x2+2x=0根的个数 ( )
(2)图象y=x2-2x+1与x轴交点个数( )
一元二次方程x2-2x+1=0根的个数( )
(3)图象y=x2-2x+2与x轴交点个数( )
一元二次方程x2-2x+2=0根的个数( )
二次函数y=x2+2x,y=x2-2x+1,y=x2-2x+2的图象如图:
y=x2+2x
y=x2-2x+1
y=x2-2x+2
自主学习二: 二次函数与x轴交点与一元二次方程的根有什么关系?
两个交点
一个交点
没有交点
△﹥0,有两个不相等实数根
△=0,有两个相等实数根
△﹤0无实数根
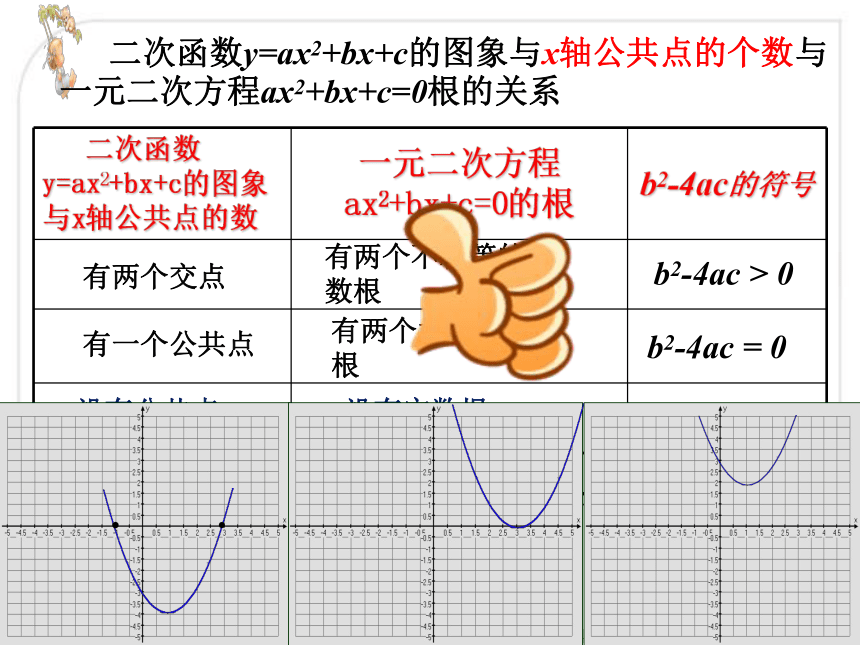
二次函数y=ax2+bx+c的图象与x轴公共点的个数与一元二次方程ax2+bx+c=0根的关系
有两个交点
有两个不相等的实数根
b2-4ac > 0
有一个公共点
有两个相等的实数根
b2-4ac = 0
没有公共点
没有实数根
b2-4ac < 0
二次函数y=ax2+bx+c的图象与x轴交点的横坐标是一元二次方程ax2+bx+c=0的根
二次函数y=ax2+bx+c的图象与x轴公共点的数 一元二次方程ax2+bx+c=0的根 b2-4ac的符号
自主学习三: 二次函数图象和x轴交点坐标与
一元二次方程的根有什么关系?
y=x2+2x与 x轴交点
X1 =-2 X2 =0
(-2,0) (0,0)
x2+2x=0方程的根是
令
y=0
交点的横坐标是一元二次方程的根
(2, 0)(4,0 )
X1 =2 X2 =4
y=x2-6x+8与x轴交点是
x2-6x+8=0方程的根是
令y=0
与x轴交点的横坐标是当y=0时自变量x的值
即方程ax2+bx+c=0的根.
二次函数y=ax2+bx+c的图象和x轴交点坐标与一元二次方ax2+bx+c=0的根有什么关系?
2.抛物线y=x2-4x+4与轴有 个交点,坐标是 。
3.抛物线y=0.5x2-x+3与x轴的交点情况是( )
A 两个交点 B 一个交点 C 没有交点 D 画出图象后才能说明
1 . 若方程ax2+bx+c=0的根为x1=-2和x2=3,则二次函数
y=ax2+bx+c的图象与x轴交点坐标是 。
(-2,0)、(3,0)
一
(2,0)
4 不画图象,求抛物线y=x2-3x-4与x轴的交点坐标。
解:∵解方程x2-3x-4=0得: x1=-1,x2=4
∴抛物线y=x2-3x-4与x轴的交点坐标是:
(-1,0)和(4,0)
跟踪练习一
5.若二次函数 图象与x 轴是只有一个公共点,求m的值.
解:∵ 图象与x 轴是只有一个公共点
则△=0
即 36-4m=0 ∴ m=9
c
1
0
1
x
y
M
N
2
3
2
y=x2-4x+4
一元二次方程x2-4x+4=1的根二次函数y=x2-4x+4的图象与直线( )交点的横坐标
能力升华
.
.
直线y=1
一元二次方程x2-4x+4=0的根是函数
y=x2-4x+4的图象与( )交点的横坐标。
1
0
x
N
2
y=x2-4x+4
.
直线y=0
直线y=0
y
方程x2-4x+4=1的根(x1= x2= )
1
3
X轴
直线y=1
?
正确
(x-2)2=1
(x-2)=±1
X-2=-1 或 x-2=1
一元二次方ax2+bx+c=k的根是函数y=ax2+bx+c
的图象和 交点横坐标
y
x
0
.
直线y=k
.
直线y=k
x1
x2
跟踪练习二
函数的图象y=ax2+bx+c如图所示, 那么
(1)关于ax2+bx+c=0的一元二次方程的根的情况是( )
(2)关于ax2+bx+c=4的一元二次方程的根的情况是( )
(3)关于ax2+bx+c=2的一元二次方程的根的情况是( )
x
y
0
4
-2
Y=0
Y=4
Y=2
2
两个不相等的实数根
无实数根
两个相等的实数根
例1.已知抛物线y=x2- 2 x-3.
(2) 利用图像回答:
(1) 作出这个函数的图像;
(Ⅰ)方程x2- 2 x-3=0的解是什么?
(Ⅱ)x取何值时y>0
(Ⅲ)x取何值时y<0
(3)在同一坐标系中画出函数y=x2- 2 x和函数y=3的图象,并求出交点的横坐标
(4)比较(2)中 (Ⅰ)与(3)的结果,你能发现什么?
能力提升
(2)x取什么值时,y>0 ?
(3)x取什么值时,y<0 ?
(4)由图像你还能获得那些信息?
①开口方向确定a
②对称轴确定a,b
③与y轴交点坐标,确定c
④ x取何值时y﹥0,y=0,y ﹤0 ⑤顶点坐标
⑥最值
⑦增减性
⑧特殊的值所得到的特殊的式子。(如x=1或x=-1)
⑨与x轴公共点个数
⑩ b ? -4ac
二次函数 的图像的一部分如图所示,图像过点A(3,0),对称轴为 ,下列结论正确的个数为( )
01 3 x
y
①b? -4ac﹥0
②bc﹤0
③2a+b=0
④a+b+c=0
⑤方程 有两个大于1的实数根
⑥当x﹥1时,y随x的增大而增大
A.1 B.2 C.3 D.4
B
2.不与x轴相交的抛物线是( )
A y=2x2 – 3 B y= - 2 x2 + 3
C y= - x2 – 3x D y=-2(x+1)2 - 3
D
随堂训练
4.在直角坐标系中,抛物线 y = 3x2+5x-2与x轴交点有( )
A、2个 B、1个 C、0个 D、无法确定
若二次函数y = kx2-7x-7的图象与x轴有
交点,则k的取值范围是___________.
A
5、判断下列函数图象与x 轴是否有公共点,
并说明理由。
(1)
(2)
(3)
解:(1)
∴该抛物线 与x轴有
两个交点。
∵a=1,b=-1,c=0
∴b?-4ac=(-1) ?-4×1×0=1>0
6.抛物线 y=2x2-3x-5 与y轴交于点____,与x轴交于点 .
7.一元二次方程 3 x2+x-10=0的两个根是x1-2 ,x2=5/3,那么二次函数 y= 3 x2+x-10与x轴的交点坐标是________.
(0,-5)
(5/2,0) (-1,0)
(-2,0) (5/3,0)
归纳:一元二次方程ax2+bx+c=0的两个根为x1,x2 ,则抛物线 y=ax2+bx+c与x轴的交点坐标是(x1,0),(x2,0)
8、若函数 图象与x 轴是只有
一个公共点,求m的值.
解:由题意知,b?-4ac=0,这里a= m, b =-6 ,c =2.
∴(-6) ?-4×m×2=0
∴m=
课堂小结
若二次函数y=ax 2+bx+c的图象和x轴交点坐标(X1 ,0) (X2 ,0),则二次函数的表达式可表示为 这种表示方法称为二次函数的交点式。
若一元二次方程ax 2+bx+c=0两个根为x 1 , x2 则一元二次方程可化为
Y=a(x-x1)(x-x2)
(x-x1)(x-x2)=0
友情提示:二次函数有哪几种表达形式?
解:
设所求的二次函数为 y=a(x+1)(x-2)
因为
点M( 0,2 )在抛物线上
所以:a(0+1)(0-2)=2
得 : a=-1
故所求的抛物线为 y=- (x+1)(x-2)
即:y=-x2+x+2
思考: 你能用什么方法做呢? 哪个方法更好?
例2
要化成
一般式
二次函数的图象与轴交于(2,0)(-1,0)且过点(0,-2)求这个二次函数的解析式
跟踪练习三
解:
设所求的二次函数为 y=a(x-2)(x+1)
因为:
点M( 0,-2 )在抛物线上
所以:a(0-2)(0+1)=-2
得 : a=1
故所求的抛物线为 y=(x-2)(x+1)
即:y=x2-x-2
课堂小结
2. 二次函数与一元二次方程的关系
y=ax2+bx+c
ax2+bx+c=k
y取定值k
方程的根
交点的横坐标
与直线y=k
1.二次函数y=ax2+bx+c与X轴交点个数的确定
3.用交点式求二次函数表达式
数形结合的思想
1、已知二次函数y=ax2+bx+c(a≠0)的图象如
下图所示,请写出方程ax2+bx+c=0(a≠0)的根
2、抛物线y=-3(x-2)(x+5)与x轴的交点坐标为
_____
3.二次函数y=kx2+4x-4的图象与x轴有交点,
则k 的取值范围 .
目标检测
相信自己,我能行
X1=-2 ,x2=1
(2,0) (-5,0)
K>-1且k≠0
4.已知二次函数图象过(-1,0),(3,0)和(1,-8)三点,求二次函数表达式。
Y=2(x+1)(x-3)
即:Y=2x2-4x-6
5.6. 二次函数的图像与一元二次方程
1、 一元二次方程ax2+bx+c=0(a≠0)的根的判别式△ = 。
方程根的情况是:当△﹥0 时方程 ;
当△=0时,方程 ;
当△﹤0时,方程 。
b2-4ac
有两个不等实数根
有两个相等实数根
没有实数根
2 、 二次函数y=ax2+bx+c(a、b、c是常数,且a≠0)图像
是一条 ,
复习提问
抛物线
3、
(0,2)
(1,0)
x
y
O
根据函数 的图像填空。
①开口方向确定a____0; ___0
②对称轴位置确定b____0;
③与y轴交点坐标,确定c =____;
④有最___值;在对称轴的右侧
y随x的增大而_____;
⑤特殊的值所得到的特殊的式子:
当x=1时,a+b+c___0,当x=-1时,
a-b+c___0 .
⑥与x轴公共点个数为____个。
当y=____时,可求出公共点的
坐标。
-1
如何确定
抛物线
与x轴有几个公共点?
<
<
<
>
减小
大
=
>
两
0
1、二次函数图像与x轴交点个数有几种情况?想一想,
画一画
y
0
三种可能:①两个交点
②一个交点
③没有交点。
自主学习一:
(1). 图象y=x2+2x与x轴交点个数( )
一元二次方程x2+2x=0根的个数 ( )
(2)图象y=x2-2x+1与x轴交点个数( )
一元二次方程x2-2x+1=0根的个数( )
(3)图象y=x2-2x+2与x轴交点个数( )
一元二次方程x2-2x+2=0根的个数( )
二次函数y=x2+2x,y=x2-2x+1,y=x2-2x+2的图象如图:
y=x2+2x
y=x2-2x+1
y=x2-2x+2
自主学习二: 二次函数与x轴交点与一元二次方程的根有什么关系?
两个交点
一个交点
没有交点
△﹥0,有两个不相等实数根
△=0,有两个相等实数根
△﹤0无实数根
二次函数y=ax2+bx+c的图象与x轴公共点的个数与一元二次方程ax2+bx+c=0根的关系
有两个交点
有两个不相等的实数根
b2-4ac > 0
有一个公共点
有两个相等的实数根
b2-4ac = 0
没有公共点
没有实数根
b2-4ac < 0
二次函数y=ax2+bx+c的图象与x轴交点的横坐标是一元二次方程ax2+bx+c=0的根
二次函数y=ax2+bx+c的图象与x轴公共点的数 一元二次方程ax2+bx+c=0的根 b2-4ac的符号
自主学习三: 二次函数图象和x轴交点坐标与
一元二次方程的根有什么关系?
y=x2+2x与 x轴交点
X1 =-2 X2 =0
(-2,0) (0,0)
x2+2x=0方程的根是
令
y=0
交点的横坐标是一元二次方程的根
(2, 0)(4,0 )
X1 =2 X2 =4
y=x2-6x+8与x轴交点是
x2-6x+8=0方程的根是
令y=0
与x轴交点的横坐标是当y=0时自变量x的值
即方程ax2+bx+c=0的根.
二次函数y=ax2+bx+c的图象和x轴交点坐标与一元二次方ax2+bx+c=0的根有什么关系?
2.抛物线y=x2-4x+4与轴有 个交点,坐标是 。
3.抛物线y=0.5x2-x+3与x轴的交点情况是( )
A 两个交点 B 一个交点 C 没有交点 D 画出图象后才能说明
1 . 若方程ax2+bx+c=0的根为x1=-2和x2=3,则二次函数
y=ax2+bx+c的图象与x轴交点坐标是 。
(-2,0)、(3,0)
一
(2,0)
4 不画图象,求抛物线y=x2-3x-4与x轴的交点坐标。
解:∵解方程x2-3x-4=0得: x1=-1,x2=4
∴抛物线y=x2-3x-4与x轴的交点坐标是:
(-1,0)和(4,0)
跟踪练习一
5.若二次函数 图象与x 轴是只有一个公共点,求m的值.
解:∵ 图象与x 轴是只有一个公共点
则△=0
即 36-4m=0 ∴ m=9
c
1
0
1
x
y
M
N
2
3
2
y=x2-4x+4
一元二次方程x2-4x+4=1的根二次函数y=x2-4x+4的图象与直线( )交点的横坐标
能力升华
.
.
直线y=1
一元二次方程x2-4x+4=0的根是函数
y=x2-4x+4的图象与( )交点的横坐标。
1
0
x
N
2
y=x2-4x+4
.
直线y=0
直线y=0
y
方程x2-4x+4=1的根(x1= x2= )
1
3
X轴
直线y=1
?
正确
(x-2)2=1
(x-2)=±1
X-2=-1 或 x-2=1
一元二次方ax2+bx+c=k的根是函数y=ax2+bx+c
的图象和 交点横坐标
y
x
0
.
直线y=k
.
直线y=k
x1
x2
跟踪练习二
函数的图象y=ax2+bx+c如图所示, 那么
(1)关于ax2+bx+c=0的一元二次方程的根的情况是( )
(2)关于ax2+bx+c=4的一元二次方程的根的情况是( )
(3)关于ax2+bx+c=2的一元二次方程的根的情况是( )
x
y
0
4
-2
Y=0
Y=4
Y=2
2
两个不相等的实数根
无实数根
两个相等的实数根
例1.已知抛物线y=x2- 2 x-3.
(2) 利用图像回答:
(1) 作出这个函数的图像;
(Ⅰ)方程x2- 2 x-3=0的解是什么?
(Ⅱ)x取何值时y>0
(Ⅲ)x取何值时y<0
(3)在同一坐标系中画出函数y=x2- 2 x和函数y=3的图象,并求出交点的横坐标
(4)比较(2)中 (Ⅰ)与(3)的结果,你能发现什么?
能力提升
(2)x取什么值时,y>0 ?
(3)x取什么值时,y<0 ?
(4)由图像你还能获得那些信息?
①开口方向确定a
②对称轴确定a,b
③与y轴交点坐标,确定c
④ x取何值时y﹥0,y=0,y ﹤0 ⑤顶点坐标
⑥最值
⑦增减性
⑧特殊的值所得到的特殊的式子。(如x=1或x=-1)
⑨与x轴公共点个数
⑩ b ? -4ac
二次函数 的图像的一部分如图所示,图像过点A(3,0),对称轴为 ,下列结论正确的个数为( )
01 3 x
y
①b? -4ac﹥0
②bc﹤0
③2a+b=0
④a+b+c=0
⑤方程 有两个大于1的实数根
⑥当x﹥1时,y随x的增大而增大
A.1 B.2 C.3 D.4
B
2.不与x轴相交的抛物线是( )
A y=2x2 – 3 B y= - 2 x2 + 3
C y= - x2 – 3x D y=-2(x+1)2 - 3
D
随堂训练
4.在直角坐标系中,抛物线 y = 3x2+5x-2与x轴交点有( )
A、2个 B、1个 C、0个 D、无法确定
若二次函数y = kx2-7x-7的图象与x轴有
交点,则k的取值范围是___________.
A
5、判断下列函数图象与x 轴是否有公共点,
并说明理由。
(1)
(2)
(3)
解:(1)
∴该抛物线 与x轴有
两个交点。
∵a=1,b=-1,c=0
∴b?-4ac=(-1) ?-4×1×0=1>0
6.抛物线 y=2x2-3x-5 与y轴交于点____,与x轴交于点 .
7.一元二次方程 3 x2+x-10=0的两个根是x1-2 ,x2=5/3,那么二次函数 y= 3 x2+x-10与x轴的交点坐标是________.
(0,-5)
(5/2,0) (-1,0)
(-2,0) (5/3,0)
归纳:一元二次方程ax2+bx+c=0的两个根为x1,x2 ,则抛物线 y=ax2+bx+c与x轴的交点坐标是(x1,0),(x2,0)
8、若函数 图象与x 轴是只有
一个公共点,求m的值.
解:由题意知,b?-4ac=0,这里a= m, b =-6 ,c =2.
∴(-6) ?-4×m×2=0
∴m=
课堂小结
若二次函数y=ax 2+bx+c的图象和x轴交点坐标(X1 ,0) (X2 ,0),则二次函数的表达式可表示为 这种表示方法称为二次函数的交点式。
若一元二次方程ax 2+bx+c=0两个根为x 1 , x2 则一元二次方程可化为
Y=a(x-x1)(x-x2)
(x-x1)(x-x2)=0
友情提示:二次函数有哪几种表达形式?
解:
设所求的二次函数为 y=a(x+1)(x-2)
因为
点M( 0,2 )在抛物线上
所以:a(0+1)(0-2)=2
得 : a=-1
故所求的抛物线为 y=- (x+1)(x-2)
即:y=-x2+x+2
思考: 你能用什么方法做呢? 哪个方法更好?
例2
要化成
一般式
二次函数的图象与轴交于(2,0)(-1,0)且过点(0,-2)求这个二次函数的解析式
跟踪练习三
解:
设所求的二次函数为 y=a(x-2)(x+1)
因为:
点M( 0,-2 )在抛物线上
所以:a(0-2)(0+1)=-2
得 : a=1
故所求的抛物线为 y=(x-2)(x+1)
即:y=x2-x-2
课堂小结
2. 二次函数与一元二次方程的关系
y=ax2+bx+c
ax2+bx+c=k
y取定值k
方程的根
交点的横坐标
与直线y=k
1.二次函数y=ax2+bx+c与X轴交点个数的确定
3.用交点式求二次函数表达式
数形结合的思想
1、已知二次函数y=ax2+bx+c(a≠0)的图象如
下图所示,请写出方程ax2+bx+c=0(a≠0)的根
2、抛物线y=-3(x-2)(x+5)与x轴的交点坐标为
_____
3.二次函数y=kx2+4x-4的图象与x轴有交点,
则k 的取值范围 .
目标检测
相信自己,我能行
X1=-2 ,x2=1
(2,0) (-5,0)
K>-1且k≠0
4.已知二次函数图象过(-1,0),(3,0)和(1,-8)三点,求二次函数表达式。
Y=2(x+1)(x-3)
即:Y=2x2-4x-6
