河北省石家庄二中2019年自主招生考试数学试题(PDF版,无答案)
文档属性
| 名称 | 河北省石家庄二中2019年自主招生考试数学试题(PDF版,无答案) |  | |
| 格式 | zip | ||
| 文件大小 | 530.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-27 14:49:32 | ||
图片预览

文档简介
石家庄二中自主招生
数学试题
(时间:70 分钟 满分:120 分)
一.选择题(每小题 2 分,共 36 分)
1.下列计算正确的是( )
A. 2 2 42a a a? ? B. 2 3 6a a a? ?
C. ? ?
2
2 4a a? ? D. ? ?
2 21 1a a? ? ?
2.小明统计了他家今年 5 月份打电话的次数及通话时间,并列出了频数分布表:
通话时间 / minx 0< 5x≤ 5< 10x≤ 10< 15x≤ 15< 20x≤
频数(通话次数) 20 16 9 5
则通话时间不超过15min 的频率为( )
A. 0.1 B. 0.4 C. 0.5 D. 0.9
3.两名同学进行了 10 次三级蛙跳测试,经计算,他们的平均成绩相同,若要比较这两名同学的成绩
哪一位更稳定,通常还需要比较他们的成绩的( )
A.众数 B.中位数 C.方差 D.以上都不对
4.如图所示的三棱柱的主视图是( )
5.若点 ? ?A a b, 在反比例函数
2
y
x
? 的图像上,则代数式 4ab ? 的值为( )
A. 2? B.0 C.2 D. 6?
6.在平面直角坐标系 xoy中,已知点 ? ?2 2P , ,点Q在 y 轴上, PQO△ 是等腰三角形,则满足条件的
点Q共有( )
A.5 个 B.2 个 C.3 个 D.4 个
7.菱形 ABCD中, 5AB ? , 120BCD ? ?∠ ,则对角线 BD的长是( )
A.20 B.10 C.5 3 D.5
DCBA
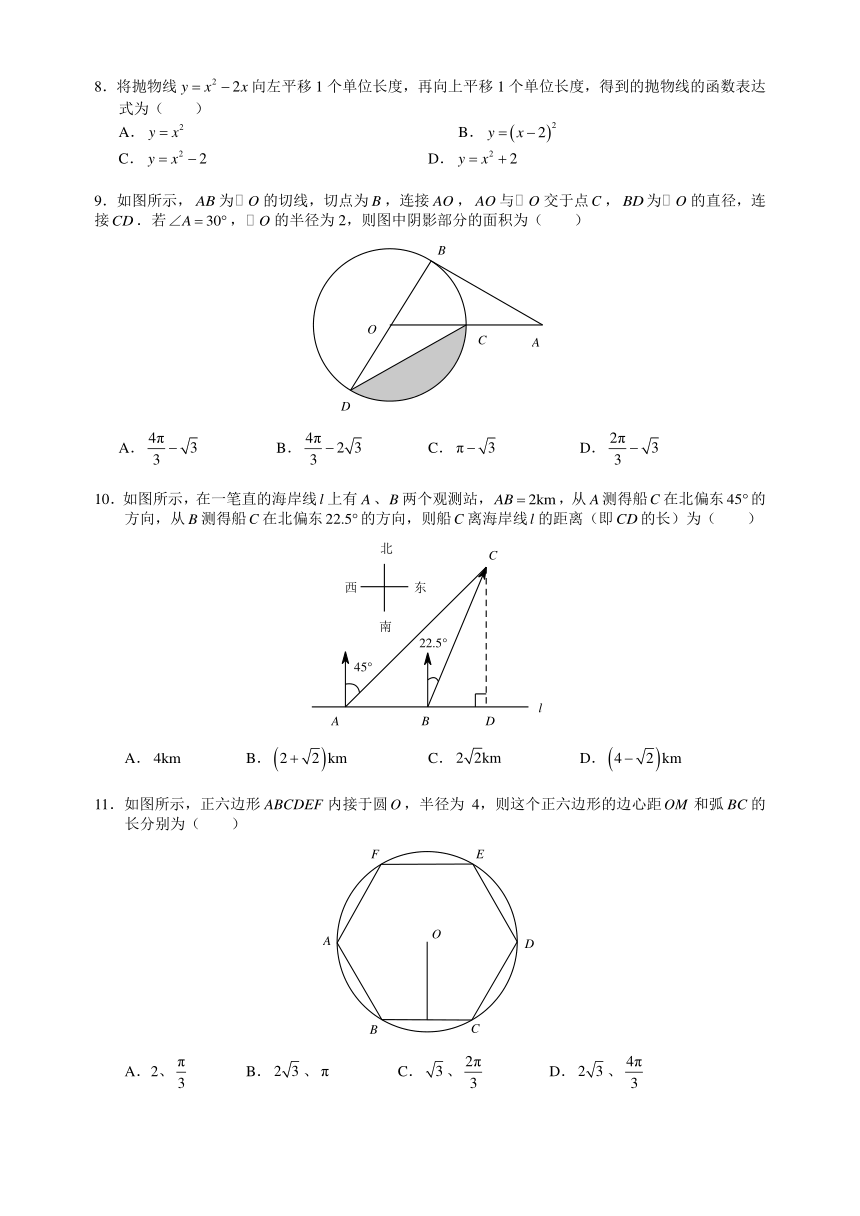
8.将抛物线 2 2y x x? ? 向左平移 1 个单位长度,再向上平移 1 个单位长度,得到的抛物线的函数表达
式为( )
A. 2y x? B. ? ?
2
2y x? ?
C. 2 2y x? ? D. 2 2y x? ?
9.如图所示, AB 为 O 的切线,切点为 B ,连接 AO , AO 与 O 交于点C ,BD为 O 的直径,连
接CD.若 30A ? ?∠ , O 的半径为 2,则图中阴影部分的面积为( )
A.
4π
3
3
? B.
4π
2 3
3
? C. π 3? D.
2π
3
3
?
10.如图所示,在一笔直的海岸线 l 上有 A、B 两个观测站, 2kmAB ? ,从 A测得船C 在北偏东 45?的
方向,从 B 测得船C 在北偏东 22.5?的方向,则船C 离海岸线 l 的距离(即CD的长)为( )
A. 4km B. ? ?2 2 km? C. 2 2km D. ? ?4 2 km?
11.如图所示,正六边形 ABCDEF 内接于圆O,半径为 4,则这个正六边形的边心距OM 和弧 BC 的
长分别为( )
A.2、
π
3
B. 2 3 、 π C. 3 、
2π
3
D. 2 3 、
4π
3
D
O
B
AC
22.5°
45°
北
西
南
东
l
A B
C
D
F E
A
B C
D
O
12.已知函数 2 2 3y x x? ? ? 在闭区间 ? ?0 m, 上有最大值 3,最小值 2,则m 的取值范围是( )
A. 1m≥ B. 0 2m≤ ≤ C.1 2m≤ ≤ D. 2m≤
13.设 >0b ,二次函数 2 2 1y ax bx a? ? ? ? 的图象下列之一:
则 a的值为( )
A.
1 5
2
? ?
B.
1 5
2
? ?
C.1 D. 1?
14.某学校要召开学生代表大会,规定各班每 10 人推选一名代表,当各班人数除以 10 的余数大于 6
时再增选一名代表.那么,各班可推选代表人数 y 与该班人数 x 之间的函数关系用取整函数 ? ?y x?
( ? ?x 表示不大于 x的最大整数)可以表示为( )
A.
10
x
y
? ?
? ? ?
? ?
B.
3
10
x
y
?? ?
? ? ?
? ?
C.
4
10
x
y
?? ?
? ? ?
? ?
D.
5
10
x
y
?? ?
? ? ?
? ?
15.如果实数 x y, 满足 ? ?? ?2 21 1 1x x y y? ? ? ? ? ,那么 x y? 的值为( )
A.0 B. 1? C.1 D.2
16.植树节某班 20 名在一段直线公路一侧植树,每人植一棵,相邻两棵树相距 10 米,开始时需将树
苗集中在某一树坑旁边,现将树坑从 1 到 20 依次编号,为使各位同学从各自树坑前来领取树苗所
走的路程总和最小,树苗可以放置的两个最佳坑位的编号为( )
A.(1)和(20) B.(9)和(10) C.(9)和(11) D.(10)和(11)
17.将 1,2,3 填入3 3× 的方格中,要求每行、每列都没有重复数字,下面是一种填法,则不同的填
写方法共有( )
A.6 B.12 C.18 D.24
18.《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周
八尺,高五尺。问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图所示,米堆为一个
圆锥的四分之一),米堆底部的弧度为 8 尺,米堆的高为 5 尺,问米堆的体积和堆放的米各为多少?”
已知 1 斛米的体积约为1.62立方尺,圆周率约为 3,估算出堆放斛的米约有( )
0
0
-1 10
-1
x
y
x
y
x
y
1
y
x
1
23 1
2 3
321
A.14 斛 B.22 斛 C.36 斛 D.66 斛
二.填空题(每小题 3 分,共 42 分)
19.比较大小:
5 1
2
?
__________
5
8
.(填“ > ”,“< ”,或“ ?”)
20.石家庄二中自主招生考试只考数学和物理,计算综合得分时,按数学占 60%,物理占 40%计算.已
知小明数学得分为 95 分,综合得分为 93 分,那么小明物理得分是__________分.
21.一次函数 ? ? ? ?3 1 5y m x m? ? ? ? 的图象不过第一象限,则实数m 的取值范围是__________.
22.使代数式
2 1x
x x
?
?
有意义 x的取值范围是__________.
23.有9张卡片,分别写有1~9这九个数字,将它们背面朝上洗匀后,任意抽出一张,记卡片上的数字
为 a,则关于 x的不等式组
? ?4 3 1
1
2 <
2
x x
x
x a
??
?
? ?
??
?
≥
有解的概率为__________.
24 . ? ?? ?2 3 2 5 4 3 25 4 3 2 1 02 3 5 6 7x x x x x a x a x a x a x a x a? ? ? ? ? ? ? ? ? ? ? , 则 0 1 2 3 4 5a a a a a a? ? ? ? ? ?
__________.
25.函数 2 22 1 4 4y x x x x? ? ? ? ? ? 的最小值为__________.
26.已知 2 3? 是方程 2 1 0x mx? ? ? 的一个实数根,则实数m 的值为__________.
27.如图所示“赵爽弦图”, ABH△ 、 BCG△ 、 CDF△ 和 DAE△ 是四个全等的直角三角形,四边形
ABCD和 EFGH 都是正方形,如果 10AB ? , 2EF ? ,那么 AH 等于__________.
28.设m?R , 1x , 2x 是方程
2 22 1 0x mx m? ? ? ? 的两个实数根,则
2 2
1 2x x? 的最小值是__________.
H
G
A B
CD
E
F
29.在平面四边形 ABCD中, 75A B C? ? ? ?∠ ∠ ∠ , 2BC ? ,则 AD 的取值范围是__________.
30.若实数m n, 满足等式
3 2
3
3 5 0
2 3
m m m
n n
? ? ? ??
?
? ???
,则m n? ? __________.
31.由数字1,2,3,4组成所有可能的没有重复数字的四位数,它们的和为__________.
32.汉诺塔问题是数学中的著名猜想之一.
如图所示:有三根针和套在一根针上的 n 个金属片,按下列规则,把金属片从一根针上全部移到
另一根针上。
(1)每次只能移动一个金属片;
(2)在每次移动过程中,每根针上较大的金属片不能放在较小的金属片上面。将 n 个金属片从1
号针移到3号针最少需要移动的次数记为 ? ?f n 。
则:(Ⅰ) ? ?3f ? __________(Ⅱ) ? ?f n ? __________.
三.解答下列各题
33.(6分)分解因式
① 22 6x x? ? ? __________
② 3 3 2x x? ? ? __________
34.(6分)解下列方程
① 2
2 1
1
1 1x x
? ?
? ?
② 2 2 2 3x x? ? ? ?
35.(6分)已知: 2 1 0x x? ? ? .
求值:①
2
2
1
x
x
? ; ② 3 22 2015x x? ?
36.(本小题满分8分)直线 y x m? ? 与双曲线
k
y
x
? .
(1)无论m 为何值,直线与双曲线都有交点,求 k 的取值范围;
(2)若直线 y x m? ? 与双曲线
k
y
x
? 的交点为 ? ?1 1A x y, , ? ?2 2B x y, , ? ?1 2 0x x? ≠ 问
1 2
1 2
y y
x x
?
?
的
值是否为定值,若是,请求出;若不是,请说明理由。
37.(本小题满分10分)
如图所示,在平面直角坐标系 xOy 中,抛物线 ? ?2 2 3 <0y ax ax a a? ? ? 与 x 轴交于 A、B 两点(点 A
在点 B 的左侧),经过点 A的直线 :l y kx b? ? 与 y 轴负半轴交于点C ,与抛物线的另一个交点为
D ,且 4CD AC? 。
(1)直接写出点 A的坐标,并求直线 l 的函数表达式(其中 k 、b 用含 a的式子表示);
12 3
数学试题
(时间:70 分钟 满分:120 分)
一.选择题(每小题 2 分,共 36 分)
1.下列计算正确的是( )
A. 2 2 42a a a? ? B. 2 3 6a a a? ?
C. ? ?
2
2 4a a? ? D. ? ?
2 21 1a a? ? ?
2.小明统计了他家今年 5 月份打电话的次数及通话时间,并列出了频数分布表:
通话时间 / minx 0< 5x≤ 5< 10x≤ 10< 15x≤ 15< 20x≤
频数(通话次数) 20 16 9 5
则通话时间不超过15min 的频率为( )
A. 0.1 B. 0.4 C. 0.5 D. 0.9
3.两名同学进行了 10 次三级蛙跳测试,经计算,他们的平均成绩相同,若要比较这两名同学的成绩
哪一位更稳定,通常还需要比较他们的成绩的( )
A.众数 B.中位数 C.方差 D.以上都不对
4.如图所示的三棱柱的主视图是( )
5.若点 ? ?A a b, 在反比例函数
2
y
x
? 的图像上,则代数式 4ab ? 的值为( )
A. 2? B.0 C.2 D. 6?
6.在平面直角坐标系 xoy中,已知点 ? ?2 2P , ,点Q在 y 轴上, PQO△ 是等腰三角形,则满足条件的
点Q共有( )
A.5 个 B.2 个 C.3 个 D.4 个
7.菱形 ABCD中, 5AB ? , 120BCD ? ?∠ ,则对角线 BD的长是( )
A.20 B.10 C.5 3 D.5
DCBA
8.将抛物线 2 2y x x? ? 向左平移 1 个单位长度,再向上平移 1 个单位长度,得到的抛物线的函数表达
式为( )
A. 2y x? B. ? ?
2
2y x? ?
C. 2 2y x? ? D. 2 2y x? ?
9.如图所示, AB 为 O 的切线,切点为 B ,连接 AO , AO 与 O 交于点C ,BD为 O 的直径,连
接CD.若 30A ? ?∠ , O 的半径为 2,则图中阴影部分的面积为( )
A.
4π
3
3
? B.
4π
2 3
3
? C. π 3? D.
2π
3
3
?
10.如图所示,在一笔直的海岸线 l 上有 A、B 两个观测站, 2kmAB ? ,从 A测得船C 在北偏东 45?的
方向,从 B 测得船C 在北偏东 22.5?的方向,则船C 离海岸线 l 的距离(即CD的长)为( )
A. 4km B. ? ?2 2 km? C. 2 2km D. ? ?4 2 km?
11.如图所示,正六边形 ABCDEF 内接于圆O,半径为 4,则这个正六边形的边心距OM 和弧 BC 的
长分别为( )
A.2、
π
3
B. 2 3 、 π C. 3 、
2π
3
D. 2 3 、
4π
3
D
O
B
AC
22.5°
45°
北
西
南
东
l
A B
C
D
F E
A
B C
D
O
12.已知函数 2 2 3y x x? ? ? 在闭区间 ? ?0 m, 上有最大值 3,最小值 2,则m 的取值范围是( )
A. 1m≥ B. 0 2m≤ ≤ C.1 2m≤ ≤ D. 2m≤
13.设 >0b ,二次函数 2 2 1y ax bx a? ? ? ? 的图象下列之一:
则 a的值为( )
A.
1 5
2
? ?
B.
1 5
2
? ?
C.1 D. 1?
14.某学校要召开学生代表大会,规定各班每 10 人推选一名代表,当各班人数除以 10 的余数大于 6
时再增选一名代表.那么,各班可推选代表人数 y 与该班人数 x 之间的函数关系用取整函数 ? ?y x?
( ? ?x 表示不大于 x的最大整数)可以表示为( )
A.
10
x
y
? ?
? ? ?
? ?
B.
3
10
x
y
?? ?
? ? ?
? ?
C.
4
10
x
y
?? ?
? ? ?
? ?
D.
5
10
x
y
?? ?
? ? ?
? ?
15.如果实数 x y, 满足 ? ?? ?2 21 1 1x x y y? ? ? ? ? ,那么 x y? 的值为( )
A.0 B. 1? C.1 D.2
16.植树节某班 20 名在一段直线公路一侧植树,每人植一棵,相邻两棵树相距 10 米,开始时需将树
苗集中在某一树坑旁边,现将树坑从 1 到 20 依次编号,为使各位同学从各自树坑前来领取树苗所
走的路程总和最小,树苗可以放置的两个最佳坑位的编号为( )
A.(1)和(20) B.(9)和(10) C.(9)和(11) D.(10)和(11)
17.将 1,2,3 填入3 3× 的方格中,要求每行、每列都没有重复数字,下面是一种填法,则不同的填
写方法共有( )
A.6 B.12 C.18 D.24
18.《九章算术》是我国古代内容极为丰富的数学名著,书中有如下问题:“今有委米依垣内角,下周
八尺,高五尺。问:积及为米几何?”其意思为:“在屋内墙角处堆放米(如图所示,米堆为一个
圆锥的四分之一),米堆底部的弧度为 8 尺,米堆的高为 5 尺,问米堆的体积和堆放的米各为多少?”
已知 1 斛米的体积约为1.62立方尺,圆周率约为 3,估算出堆放斛的米约有( )
0
0
-1 10
-1
x
y
x
y
x
y
1
y
x
1
23 1
2 3
321
A.14 斛 B.22 斛 C.36 斛 D.66 斛
二.填空题(每小题 3 分,共 42 分)
19.比较大小:
5 1
2
?
__________
5
8
.(填“ > ”,“< ”,或“ ?”)
20.石家庄二中自主招生考试只考数学和物理,计算综合得分时,按数学占 60%,物理占 40%计算.已
知小明数学得分为 95 分,综合得分为 93 分,那么小明物理得分是__________分.
21.一次函数 ? ? ? ?3 1 5y m x m? ? ? ? 的图象不过第一象限,则实数m 的取值范围是__________.
22.使代数式
2 1x
x x
?
?
有意义 x的取值范围是__________.
23.有9张卡片,分别写有1~9这九个数字,将它们背面朝上洗匀后,任意抽出一张,记卡片上的数字
为 a,则关于 x的不等式组
? ?4 3 1
1
2 <
2
x x
x
x a
??
?
? ?
??
?
≥
有解的概率为__________.
24 . ? ?? ?2 3 2 5 4 3 25 4 3 2 1 02 3 5 6 7x x x x x a x a x a x a x a x a? ? ? ? ? ? ? ? ? ? ? , 则 0 1 2 3 4 5a a a a a a? ? ? ? ? ?
__________.
25.函数 2 22 1 4 4y x x x x? ? ? ? ? ? 的最小值为__________.
26.已知 2 3? 是方程 2 1 0x mx? ? ? 的一个实数根,则实数m 的值为__________.
27.如图所示“赵爽弦图”, ABH△ 、 BCG△ 、 CDF△ 和 DAE△ 是四个全等的直角三角形,四边形
ABCD和 EFGH 都是正方形,如果 10AB ? , 2EF ? ,那么 AH 等于__________.
28.设m?R , 1x , 2x 是方程
2 22 1 0x mx m? ? ? ? 的两个实数根,则
2 2
1 2x x? 的最小值是__________.
H
G
A B
CD
E
F
29.在平面四边形 ABCD中, 75A B C? ? ? ?∠ ∠ ∠ , 2BC ? ,则 AD 的取值范围是__________.
30.若实数m n, 满足等式
3 2
3
3 5 0
2 3
m m m
n n
? ? ? ??
?
? ???
,则m n? ? __________.
31.由数字1,2,3,4组成所有可能的没有重复数字的四位数,它们的和为__________.
32.汉诺塔问题是数学中的著名猜想之一.
如图所示:有三根针和套在一根针上的 n 个金属片,按下列规则,把金属片从一根针上全部移到
另一根针上。
(1)每次只能移动一个金属片;
(2)在每次移动过程中,每根针上较大的金属片不能放在较小的金属片上面。将 n 个金属片从1
号针移到3号针最少需要移动的次数记为 ? ?f n 。
则:(Ⅰ) ? ?3f ? __________(Ⅱ) ? ?f n ? __________.
三.解答下列各题
33.(6分)分解因式
① 22 6x x? ? ? __________
② 3 3 2x x? ? ? __________
34.(6分)解下列方程
① 2
2 1
1
1 1x x
? ?
? ?
② 2 2 2 3x x? ? ? ?
35.(6分)已知: 2 1 0x x? ? ? .
求值:①
2
2
1
x
x
? ; ② 3 22 2015x x? ?
36.(本小题满分8分)直线 y x m? ? 与双曲线
k
y
x
? .
(1)无论m 为何值,直线与双曲线都有交点,求 k 的取值范围;
(2)若直线 y x m? ? 与双曲线
k
y
x
? 的交点为 ? ?1 1A x y, , ? ?2 2B x y, , ? ?1 2 0x x? ≠ 问
1 2
1 2
y y
x x
?
?
的
值是否为定值,若是,请求出;若不是,请说明理由。
37.(本小题满分10分)
如图所示,在平面直角坐标系 xOy 中,抛物线 ? ?2 2 3 <0y ax ax a a? ? ? 与 x 轴交于 A、B 两点(点 A
在点 B 的左侧),经过点 A的直线 :l y kx b? ? 与 y 轴负半轴交于点C ,与抛物线的另一个交点为
D ,且 4CD AC? 。
(1)直接写出点 A的坐标,并求直线 l 的函数表达式(其中 k 、b 用含 a的式子表示);
12 3
同课章节目录
