5.2.2 平行线的判定课件
图片预览




文档简介
(共18张PPT)
复习引入
1、两直线的位置关系有哪几种?
2、怎样的两条直线平行?
3、平行线的公理及推论是什么?
探究新知
1
2
a
b
.
A
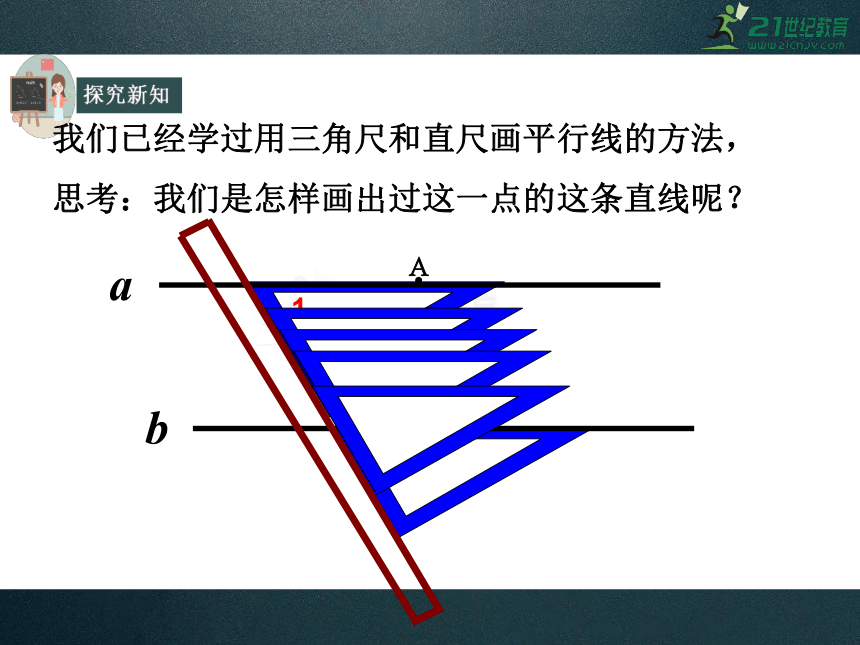
我们已经学过用三角尺和直尺画平行线的方法,
思考:我们是怎样画出过这一点的这条直线呢?
探究新知
1、∠1和∠2是什么位置关系的角?
2、在三角板移动的过程中,∠1和∠2的大小发生变化了吗?
3、要判断a//b你有办法了吗?
没有发生变化
∠1和∠2是同位角
探究新知
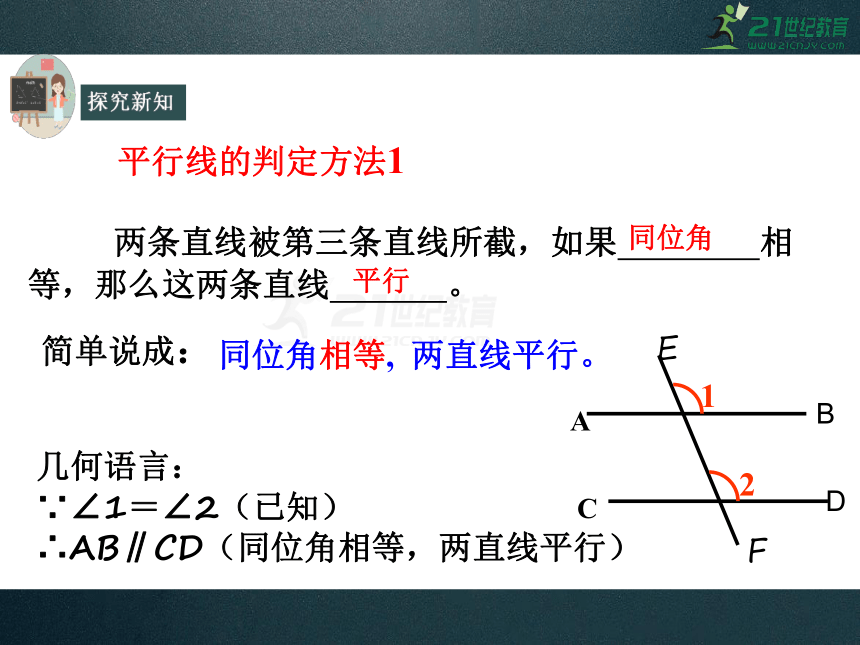
两条直线被第三条直线所截,如果 相等,那么这两条直线 。
简单说成:
同位角相等, 两直线平行。
平行线的判定方法1
同位角
平行
几何语言:
∵∠1=∠2(已知)
∴AB∥CD(同位角相等,两直线平行)
做一做
1.如图,∠1=∠2=55°,∠3等于多少度?直线AB,CD平行吗?说明你的理由。
几何语言表述:
探究新知
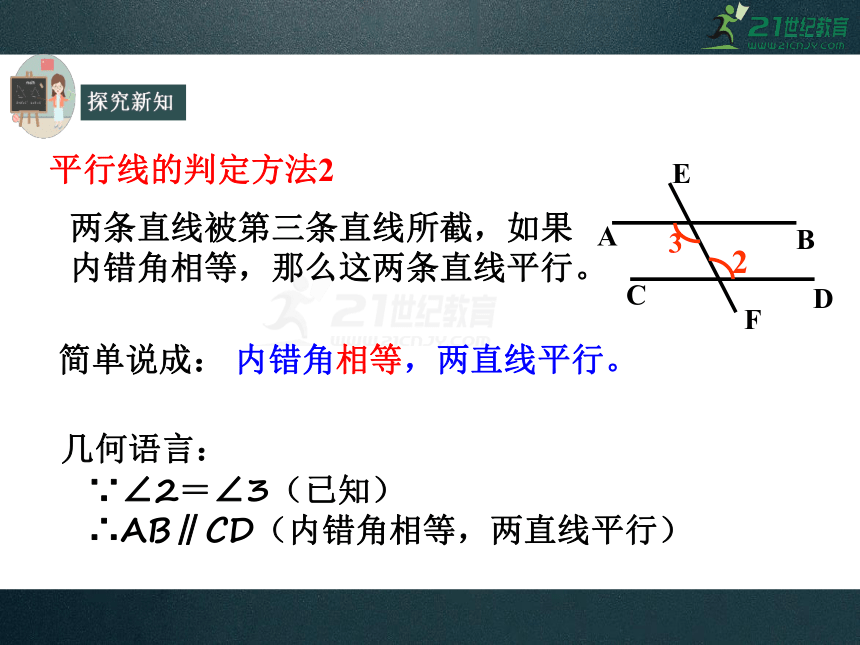
平行线的判定方法2
两条直线被第三条直线所截,如果
内错角相等,那么这两条直线平行。
内错角相等,两直线平行。
简单说成:
几何语言:
∵∠2=∠3(已知)
∴AB∥CD(内错角相等,两直线平行)
做一做
如图: 如果∠1=∠3, 那么a与b平行吗?
几何语言表述:
探究新知
简单说成:
同旁内角互补,两直线平行。
平行线的判定方法3
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行。
几何语言:
∵∠2+∠4=180°(已知)
∴a∥b(同旁内角互补,两直线平行)
做一做
如图:如果∠1+∠2=180o,
那么a与b平行吗?
几何语言表述:
探究新知
总结判定两条直线平行的方法
同位角
内错角
同旁内角
∠1=∠2
∠3=∠2
∠2+∠4=180°
文字叙述 符号语言 图形
相等两直线平行 ∵ (已知)
∴a∥b
相等
两直线平行 ∵ (已知)
∴a∥b
互补,两直线平行 ∵
∴a∥b
随堂训练
1、如图:已知 ∠1=65o , ∠2 =115o ,问:AB与CD平行吗?为什么?
解:∵∠2与∠5是对顶角,∠2=115°
∴∠2=∠5=115°
∵∠1=65°(已知)
又∵ ∠1+∠5=65°+115°=180°
∴ AB∥CD(同旁内角互补,两直线平行)
随堂训练
2、在同一平面内,两条直线垂直于同一条直线,这两条直线平行吗?为什么?
答:垂直于同一条直线的两条直线平行.
理由:方法一
如图,
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴b∥c(同位角相等,两直线平行)
a
b
c
1
2
随堂训练
理由:如图,
∵ b⊥a,c⊥a(已知)
∴∠1=90°,∠2=90 °(垂直定义)
∴∠1=∠2
∴b∥c(内错角相等,两直线平行)
方法二
随堂训练
理由:如图,
∵ b⊥a,c⊥a(已知)
∴∠1=90°,∠2=90°(垂直定义)
∴∠1+∠2=180°
∴b∥c(同旁内角互补,两直线平行)
方法三
从中可以得出什么结论?
在同一平面内,如果两条直线都和第三条直线垂直,那么这两条直线平行。
拓展延伸
已知∠3=60 °,∠1与∠2是对顶角,∠1+∠2=120°,试说明AB∥CD。 ?
解:∵∠1与∠2是对顶角,
∴∠1=∠2
又∵∠1+∠2=120°(已知)
∴∠1=∠2=60°
∵ ∠3=60°(已知)
∴∠ 2=∠3
∴ AB∥CD(内错角相等,两直线平行)
1
2
3
A
B
C
D
课堂小结
两直线平行
平行线的判定示意图
判定
位置关系
https://www.21cnjy.com/help/help_extract.php
复习引入
1、两直线的位置关系有哪几种?
2、怎样的两条直线平行?
3、平行线的公理及推论是什么?
探究新知
1
2
a
b
.
A
我们已经学过用三角尺和直尺画平行线的方法,
思考:我们是怎样画出过这一点的这条直线呢?
探究新知
1、∠1和∠2是什么位置关系的角?
2、在三角板移动的过程中,∠1和∠2的大小发生变化了吗?
3、要判断a//b你有办法了吗?
没有发生变化
∠1和∠2是同位角
探究新知
两条直线被第三条直线所截,如果 相等,那么这两条直线 。
简单说成:
同位角相等, 两直线平行。
平行线的判定方法1
同位角
平行
几何语言:
∵∠1=∠2(已知)
∴AB∥CD(同位角相等,两直线平行)
做一做
1.如图,∠1=∠2=55°,∠3等于多少度?直线AB,CD平行吗?说明你的理由。
几何语言表述:
探究新知
平行线的判定方法2
两条直线被第三条直线所截,如果
内错角相等,那么这两条直线平行。
内错角相等,两直线平行。
简单说成:
几何语言:
∵∠2=∠3(已知)
∴AB∥CD(内错角相等,两直线平行)
做一做
如图: 如果∠1=∠3, 那么a与b平行吗?
几何语言表述:
探究新知
简单说成:
同旁内角互补,两直线平行。
平行线的判定方法3
两条直线被第三条直线所截,如果同旁内角互补,那么这两条直线平行。
几何语言:
∵∠2+∠4=180°(已知)
∴a∥b(同旁内角互补,两直线平行)
做一做
如图:如果∠1+∠2=180o,
那么a与b平行吗?
几何语言表述:
探究新知
总结判定两条直线平行的方法
同位角
内错角
同旁内角
∠1=∠2
∠3=∠2
∠2+∠4=180°
文字叙述 符号语言 图形
相等两直线平行 ∵ (已知)
∴a∥b
相等
两直线平行 ∵ (已知)
∴a∥b
互补,两直线平行 ∵
∴a∥b
随堂训练
1、如图:已知 ∠1=65o , ∠2 =115o ,问:AB与CD平行吗?为什么?
解:∵∠2与∠5是对顶角,∠2=115°
∴∠2=∠5=115°
∵∠1=65°(已知)
又∵ ∠1+∠5=65°+115°=180°
∴ AB∥CD(同旁内角互补,两直线平行)
随堂训练
2、在同一平面内,两条直线垂直于同一条直线,这两条直线平行吗?为什么?
答:垂直于同一条直线的两条直线平行.
理由:方法一
如图,
∵ b⊥a,c⊥a(已知)
∴∠1=∠2=90°(垂直定义)
∴b∥c(同位角相等,两直线平行)
a
b
c
1
2
随堂训练
理由:如图,
∵ b⊥a,c⊥a(已知)
∴∠1=90°,∠2=90 °(垂直定义)
∴∠1=∠2
∴b∥c(内错角相等,两直线平行)
方法二
随堂训练
理由:如图,
∵ b⊥a,c⊥a(已知)
∴∠1=90°,∠2=90°(垂直定义)
∴∠1+∠2=180°
∴b∥c(同旁内角互补,两直线平行)
方法三
从中可以得出什么结论?
在同一平面内,如果两条直线都和第三条直线垂直,那么这两条直线平行。
拓展延伸
已知∠3=60 °,∠1与∠2是对顶角,∠1+∠2=120°,试说明AB∥CD。 ?
解:∵∠1与∠2是对顶角,
∴∠1=∠2
又∵∠1+∠2=120°(已知)
∴∠1=∠2=60°
∵ ∠3=60°(已知)
∴∠ 2=∠3
∴ AB∥CD(内错角相等,两直线平行)
1
2
3
A
B
C
D
课堂小结
两直线平行
平行线的判定示意图
判定
位置关系
https://www.21cnjy.com/help/help_extract.php
