13.4 课题学习 最短路径问题课件
图片预览


文档简介
(共16张PPT)
人教版 初中数学
轴对称之路径最短问题
情景引入
将军从图中的马棚地出发,牵着马到一条笔直的河边某处饮水,然后回军营.请问应该在河边什么地方饮水可使他所走的路径全程最短?
军营
河
马棚
早在古罗马时代,传说亚历山大城有一位精通数学和物理的学者,名叫海伦.一天,一位罗马将军专程去拜访他,向他请教一个百思不得其解的问题:
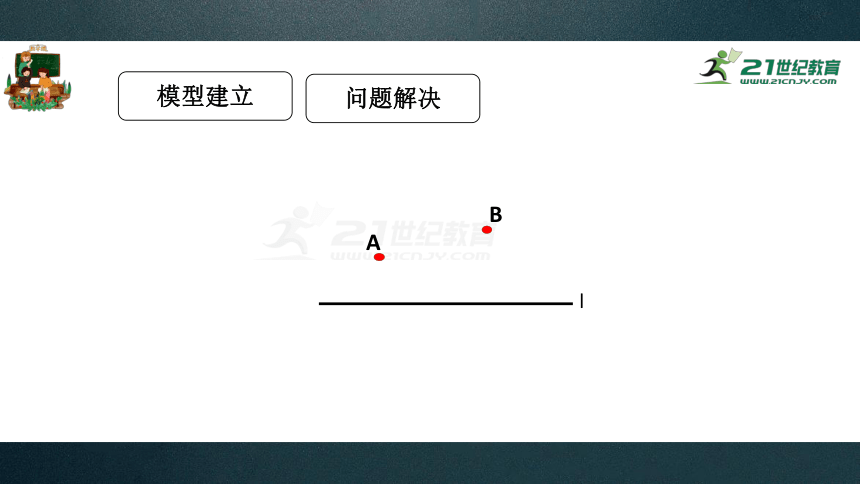
模型建立
A
B
l
问题解决
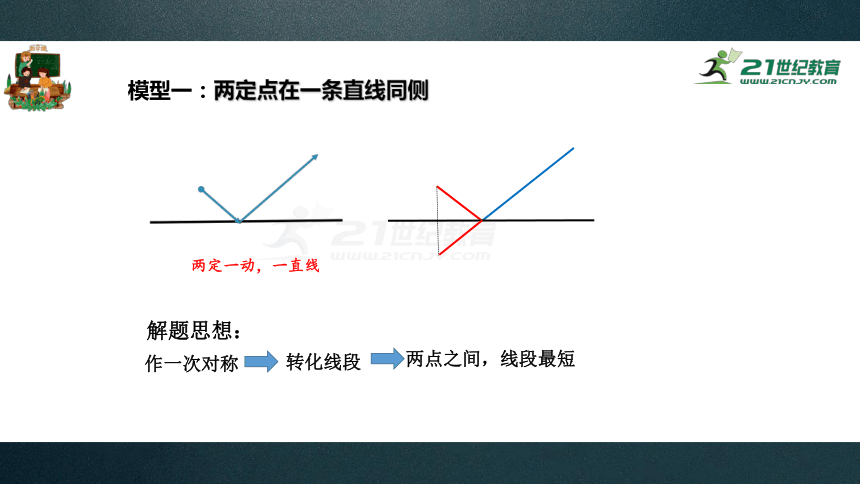
两定一动,一直线
模型一:两定点在一条直线同侧
解题思想:
作一次对称
转化线段
两点之间,线段最短
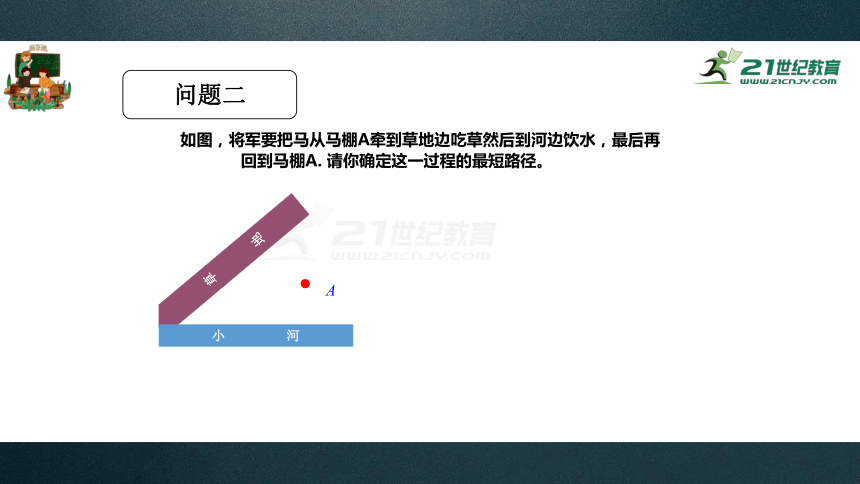
问题二
如图,将军要把马从马棚A牵到草地边吃草然后到河边饮水,最后再回到马棚A. 请你确定这一过程的最短路径。
草 地
小 河
A
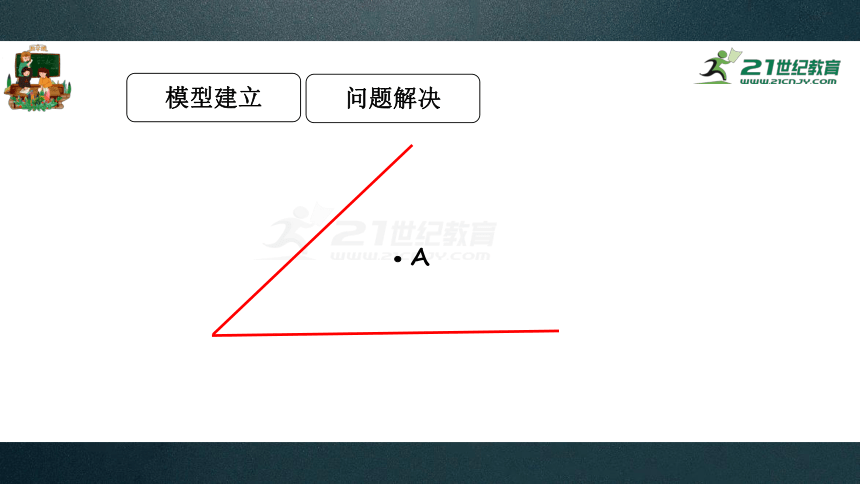
模型建立
问题解决
A
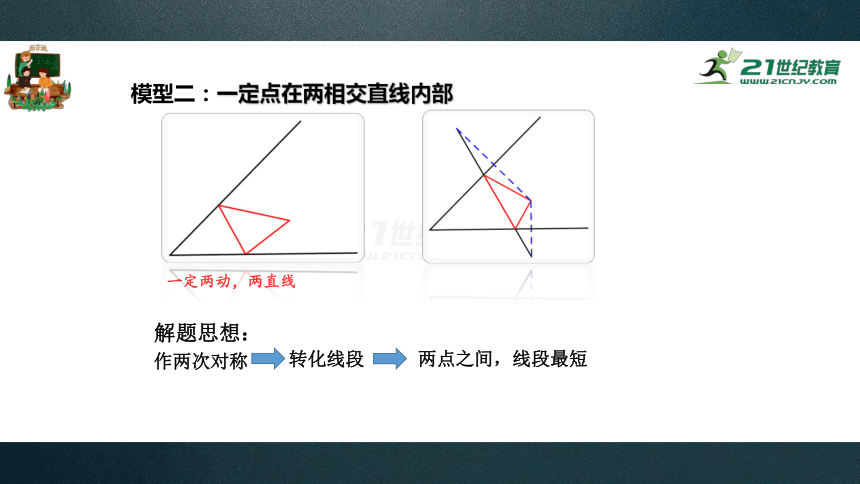
一定两动,两直线
模型二:一定点在两相交直线内部
解题思想:
作两次对称
转化线段
两点之间,线段最短
A
B
l
M
N
如图:将军要从马棚A牵出马到草地边吃草,再到河边饮水,最后回到军营B,请你帮他确定这一天的最短路线。
l2
l1
问题三
模型建立
问题解决
A
B
两定两动,两直线
模型三:两定点在两相交直线内部
解题思想:
作两次对称
转化线段
两点之间,线段最短
两定一动,一直线
一定两动,两直线
两定两动,两直线
问题四
如图:营地附近只有沿着河边有草,将军要从马棚A牵出马到河边草地吃草,马要吃饱需要沿着河边走一段固定的长度,最后回到军营B,请你帮他确定这一天的最短路线。
军营
河
马棚
d
B
A
模型建立
问题解决
A
B
问题解决
已知A、B是两个定点,在定直线l上找两个动点M、N,且MN长度等于定长d(动点M在动点N左侧),使AM+MN+NB最小。
问题四
(造桥选址)将军每日需骑马从军营出发,去河岸对侧的瞭望台观察敌情,已知河流的宽度为30米,请问:在何地修浮桥,可使得将军每日的行程最短?
人教版 初中数学
轴对称之路径最短问题
情景引入
将军从图中的马棚地出发,牵着马到一条笔直的河边某处饮水,然后回军营.请问应该在河边什么地方饮水可使他所走的路径全程最短?
军营
河
马棚
早在古罗马时代,传说亚历山大城有一位精通数学和物理的学者,名叫海伦.一天,一位罗马将军专程去拜访他,向他请教一个百思不得其解的问题:
模型建立
A
B
l
问题解决
两定一动,一直线
模型一:两定点在一条直线同侧
解题思想:
作一次对称
转化线段
两点之间,线段最短
问题二
如图,将军要把马从马棚A牵到草地边吃草然后到河边饮水,最后再回到马棚A. 请你确定这一过程的最短路径。
草 地
小 河
A
模型建立
问题解决
A
一定两动,两直线
模型二:一定点在两相交直线内部
解题思想:
作两次对称
转化线段
两点之间,线段最短
A
B
l
M
N
如图:将军要从马棚A牵出马到草地边吃草,再到河边饮水,最后回到军营B,请你帮他确定这一天的最短路线。
l2
l1
问题三
模型建立
问题解决
A
B
两定两动,两直线
模型三:两定点在两相交直线内部
解题思想:
作两次对称
转化线段
两点之间,线段最短
两定一动,一直线
一定两动,两直线
两定两动,两直线
问题四
如图:营地附近只有沿着河边有草,将军要从马棚A牵出马到河边草地吃草,马要吃饱需要沿着河边走一段固定的长度,最后回到军营B,请你帮他确定这一天的最短路线。
军营
河
马棚
d
B
A
模型建立
问题解决
A
B
问题解决
已知A、B是两个定点,在定直线l上找两个动点M、N,且MN长度等于定长d(动点M在动点N左侧),使AM+MN+NB最小。
问题四
(造桥选址)将军每日需骑马从军营出发,去河岸对侧的瞭望台观察敌情,已知河流的宽度为30米,请问:在何地修浮桥,可使得将军每日的行程最短?
