5.3.1 平行线的性质课件
图片预览




文档简介
(共16张PPT)
情境引入
现有一个平行四边形池塘,但有个底角处填满了土,只剩下三个完整的角,你能否设法求出该平行四边形池塘的四个角各是多少度吗?
探究新知
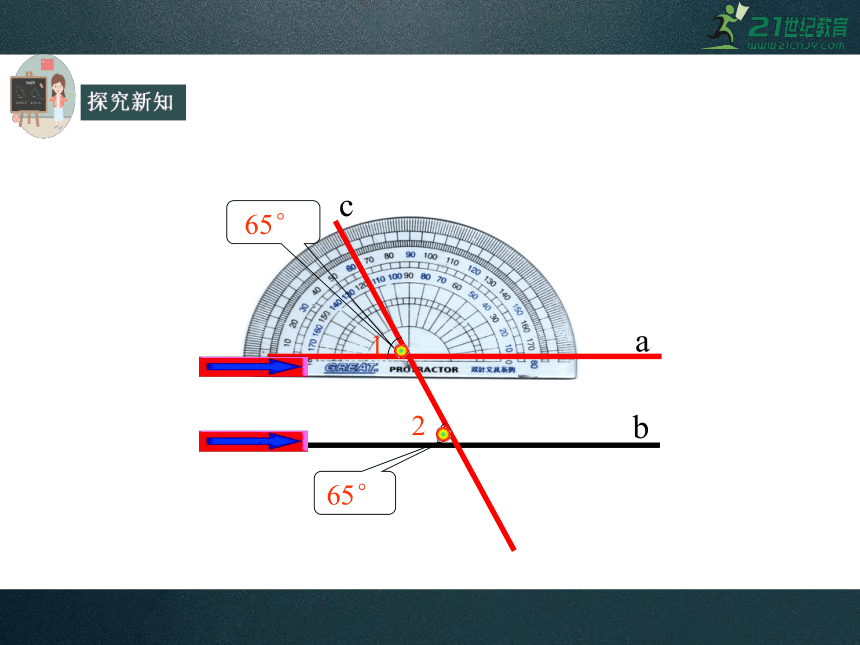
利用坐标纸上的直线或者用直尺和三角尺画两条平行线a∥b,画一条截线c与这两条平行线相交,形成了8个角.
探究新知
65°
65°
c
a
b
1
2
探究新知
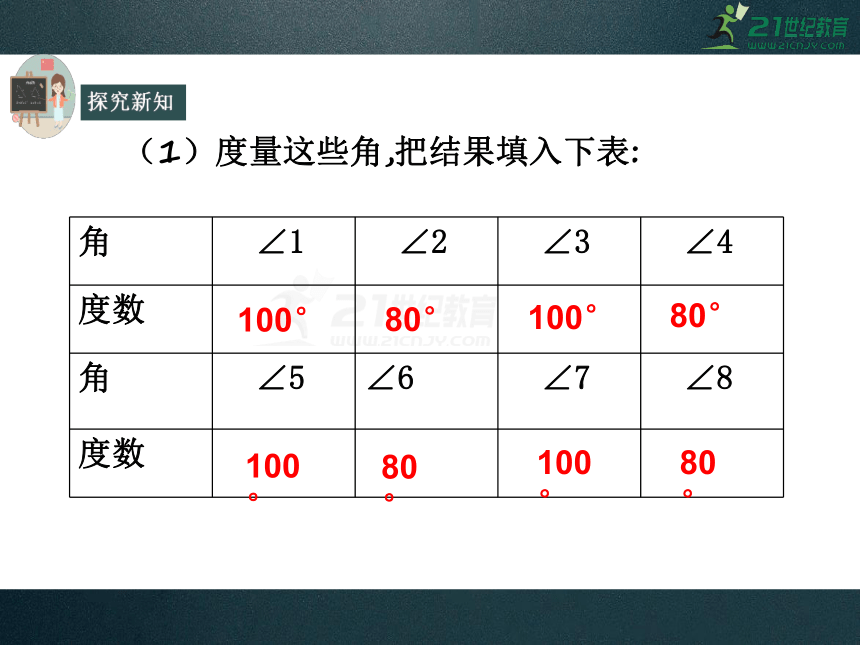
(1)度量这些角,把结果填入下表:
100°
80°
100°
80°
80°
80°
100°
100°
角 ∠1 ∠2 ∠3 ∠4
度数
角 ∠5 ∠6 ∠7 ∠8
度数
探究新知
两直线平行,同位角相等.
两条平行线被第三条直线所截,同位角相等.
简写为:
(2)比较同位角∠1和∠5的大小它们有什么关系?图中还有其他同位角吗?它们的大小有什么关系?
相等
由此猜想:
a//b ∠1= ∠5, ∠2= ∠6,
∠3= ∠7, ∠4= ∠8
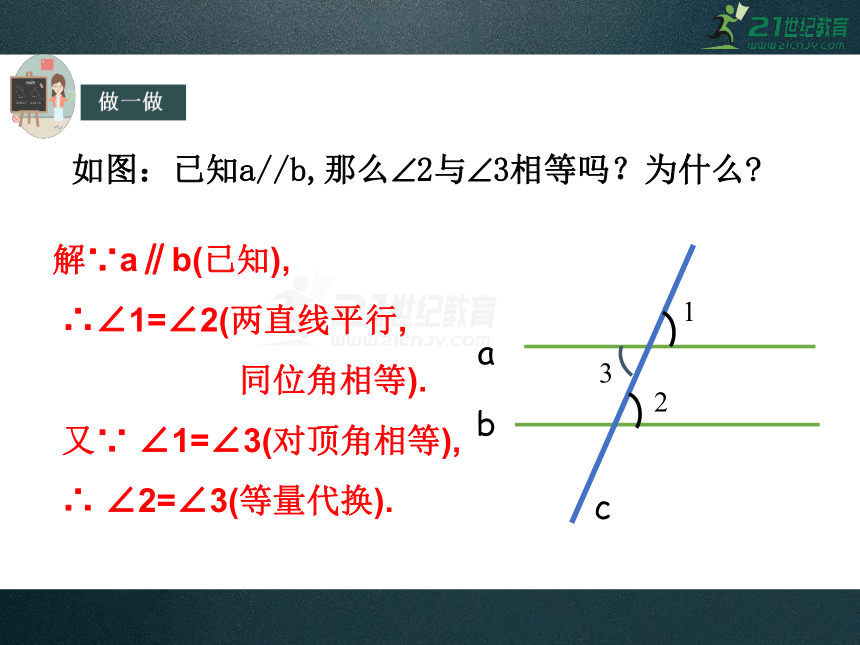
做一做
解∵a∥b(已知),
∴∠1=∠2(两直线平行,
同位角相等).
又∵ ∠1=∠3(对顶角相等),
∴ ∠2=∠3(等量代换).
如图:已知a//b,那么?2与?3相等吗?为什么?
探究新知
两直线平行,内错角相等.
平行线的性质2
两条平行线被第三条直线所截,
内错角相等.
∴∠2=∠3.
∵a∥b,
简写为:
结论
做一做
解: ∵a//b (已知),
如图,已知a//b,那么?2与?4有什么关系呢?为什么?
∴? 1= ? 2(两直线平行,同位角相等)。
∴? 2+ ? 4=180°(等量代换)。
∵ ? 1+ ? 4=180°
探究新知
两直线平行,同旁内角互补.
平行线的性质3
两条平行线被第三条直线所截,
同旁内角互补.
∴? 2+ ? 4=180°.
∵a∥b,
简写为:
结论
探究新知
两直线平行
判定
性质
已知
结论
结论
已知
平行线的性质与判定的区别:
同位角相等
内错角相等
同旁内角互补
归纳
随堂训练
1、 如图,已知直线a∥b,
∠1 = 650, 求∠2的度数.
a
b
c
1
解:∵ a∥b(已知),
∴∠ 1= ∠ 2= 500
(两直线平行,同位角相等).
随堂训练
解:
∠2=∠1 =75° (对顶角相等)
∵ a∥b(已知)
∴∠4=∠2=54°(两直线平行,内错角相等)
1、如图,直线a∥b, ∠1=75°, ∠4是多少度?
拓展延伸
A
D
解:∵AD∥BC AB∥CD ∠B=65°
∴∠A+∠B=180° ∠B+∠C=180°
∠D+∠C=180°(两直线平行,同旁内角互补)
∴∠A=180°-∠B=180°-65°=115°
如右图,AD∥BC,AB∥CD,∠B=65°,试问∠A、∠C、∠D的度数是多少?
∴∠C=180°-∠B=180°-65°=115°
∴∠D=180°-∠C=180°-115°=65°
课堂小结
图形
已知
结果
理由
同位角
内错角
同旁内角
两直线平行,
同旁内角互补
1
2
2
3
2
4
)
)
)
)
)
)
a
b
a
b
a
b
c
c
c
平行线的性质
a//b
两直线平行,
同位角相等
a//b
两直线平行,
内错角相等
a//b
∠1=∠2
∠3=∠2
∠4+∠2=180°
https://www.21cnjy.com/help/help_extract.php
情境引入
现有一个平行四边形池塘,但有个底角处填满了土,只剩下三个完整的角,你能否设法求出该平行四边形池塘的四个角各是多少度吗?
探究新知
利用坐标纸上的直线或者用直尺和三角尺画两条平行线a∥b,画一条截线c与这两条平行线相交,形成了8个角.
探究新知
65°
65°
c
a
b
1
2
探究新知
(1)度量这些角,把结果填入下表:
100°
80°
100°
80°
80°
80°
100°
100°
角 ∠1 ∠2 ∠3 ∠4
度数
角 ∠5 ∠6 ∠7 ∠8
度数
探究新知
两直线平行,同位角相等.
两条平行线被第三条直线所截,同位角相等.
简写为:
(2)比较同位角∠1和∠5的大小它们有什么关系?图中还有其他同位角吗?它们的大小有什么关系?
相等
由此猜想:
a//b ∠1= ∠5, ∠2= ∠6,
∠3= ∠7, ∠4= ∠8
做一做
解∵a∥b(已知),
∴∠1=∠2(两直线平行,
同位角相等).
又∵ ∠1=∠3(对顶角相等),
∴ ∠2=∠3(等量代换).
如图:已知a//b,那么?2与?3相等吗?为什么?
探究新知
两直线平行,内错角相等.
平行线的性质2
两条平行线被第三条直线所截,
内错角相等.
∴∠2=∠3.
∵a∥b,
简写为:
结论
做一做
解: ∵a//b (已知),
如图,已知a//b,那么?2与?4有什么关系呢?为什么?
∴? 1= ? 2(两直线平行,同位角相等)。
∴? 2+ ? 4=180°(等量代换)。
∵ ? 1+ ? 4=180°
探究新知
两直线平行,同旁内角互补.
平行线的性质3
两条平行线被第三条直线所截,
同旁内角互补.
∴? 2+ ? 4=180°.
∵a∥b,
简写为:
结论
探究新知
两直线平行
判定
性质
已知
结论
结论
已知
平行线的性质与判定的区别:
同位角相等
内错角相等
同旁内角互补
归纳
随堂训练
1、 如图,已知直线a∥b,
∠1 = 650, 求∠2的度数.
a
b
c
1
解:∵ a∥b(已知),
∴∠ 1= ∠ 2= 500
(两直线平行,同位角相等).
随堂训练
解:
∠2=∠1 =75° (对顶角相等)
∵ a∥b(已知)
∴∠4=∠2=54°(两直线平行,内错角相等)
1、如图,直线a∥b, ∠1=75°, ∠4是多少度?
拓展延伸
A
D
解:∵AD∥BC AB∥CD ∠B=65°
∴∠A+∠B=180° ∠B+∠C=180°
∠D+∠C=180°(两直线平行,同旁内角互补)
∴∠A=180°-∠B=180°-65°=115°
如右图,AD∥BC,AB∥CD,∠B=65°,试问∠A、∠C、∠D的度数是多少?
∴∠C=180°-∠B=180°-65°=115°
∴∠D=180°-∠C=180°-115°=65°
课堂小结
图形
已知
结果
理由
同位角
内错角
同旁内角
两直线平行,
同旁内角互补
1
2
2
3
2
4
)
)
)
)
)
)
a
b
a
b
a
b
c
c
c
平行线的性质
a//b
两直线平行,
同位角相等
a//b
两直线平行,
内错角相等
a//b
∠1=∠2
∠3=∠2
∠4+∠2=180°
https://www.21cnjy.com/help/help_extract.php
