27.2.1 相似三角形的判定 同步练习(解析版)
文档属性
| 名称 | 27.2.1 相似三角形的判定 同步练习(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-29 09:25:11 | ||
图片预览


文档简介
初中数学人教版九年级下学期 第二十七章 27.2.1 相似三角形的判定
一、单选题
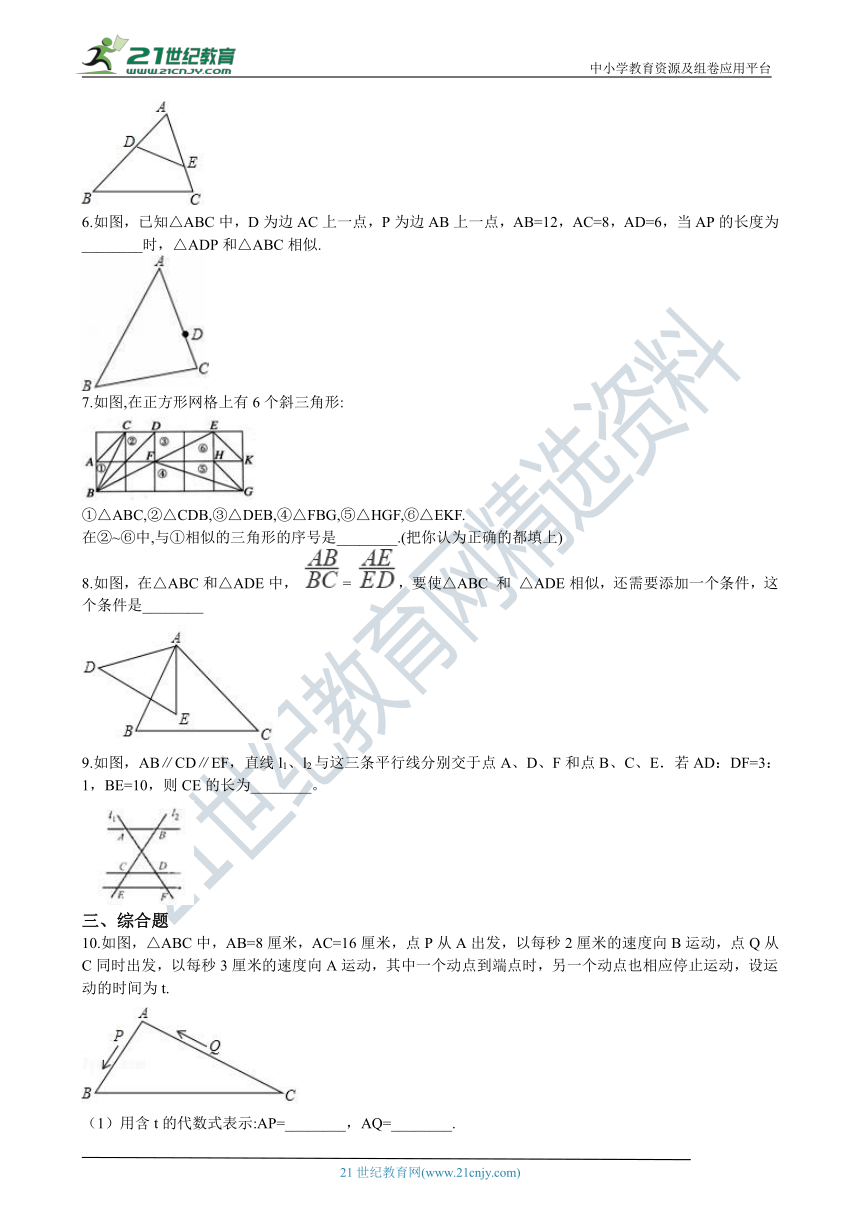
1.下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与△ABC相似的三角形所在的网格图形是(?? ) 21世纪教育网版权所有
A.???????????????????B.???????????????????C.???????????????????D.?
2.如图,BE、CD相交于点A , 连接BC , DE , 下列条件中不能判断△ABC∽ADE的是(?? )
A.?∠B=∠D???????????????????????B.?∠C=∠E???????????????????????C.????????????????????????D.?
3.如图,AB∥EF∥DC,AD∥BC,EF与AC交于点G,则是相似三角形共有(?? )
A.?3对???????????????????????????????????????B.?5对???????????????????????????????????????C.?6对???????????????????????????????????????D.?8对
4.如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,且DE∥BC,EF∥A
B.若AD=2BD,则 的值为(? )
A.???????????????????????????????????????????B.???????????????????????????????????????????C.???????????????????????????????????????????D.?
二、填空题
5.如图,添加一个条件:________,使△ADE∽△ACB.
6.如图,已知△ABC中,D为边AC上一点,P为边AB上一点,AB=12,AC=8,AD=6,当AP的长度为________时,△ADP和△ABC相似. www.21-cn-jy.com
7.如图,在正方形网格上有6个斜三角形:
①△ABC,②△CDB,③△DEB,④△FBG,⑤△HGF,⑥△EKF.
在②~⑥中,与①相似的三角形的序号是________.(把你认为正确的都填上)
8.如图,在△ABC和△ADE中, = ,要使△ABC 和 △ADE相似,还需要添加一个条件,这个条件是________ 21教育网
9.如图,AB∥CD∥EF,直线l1、l2与这三条平行线分别交于点A、D、F和点B、C、E.若AD:DF=3:1,BE=10,则CE的长为________。 2·1·c·n·j·y
三、综合题
10.如图,△ABC中,AB=8厘米,AC=16厘米,点P从A出发,以每秒2厘米的速度向B运动,点Q从C同时出发,以每秒3厘米的速度向A运动,其中一个动点到端点时,另一个动点也相应停止运动,设运动的时间为t. 21·世纪*教育网
(1)用含t的代数式表示:AP=________,AQ=________.
(2)当以A,P,Q为顶点的三角形与△ABC相似时,求运动时间是多少?
答案解析部分
一、单选题
1. C
解:根据勾股定理,AC= ,
所以,夹直角的两边的比为 =2,
观各选项,只有C选项三角形符合,与所给图形的三角形相似.
故答案为:C .
【分析】先求出两条直角边AC、BC的长度,进而求出其比值,然后利用”两边对应成比例且夹角相等的两个三角形相似”作出判断。2-1-c-n-j-y
2. C
解:∵∠BAC=∠DAE,
∴当∠B=∠D或∠C=∠E时,可利用两角对应相等的两个三角形相似证得△ABC∽ADE,故A、B选项可判断两三角形相似;【来源:21cnj*y.co*m】
当 时,可得 ,结合∠BAC=∠DAE,则可证得△ABC∽△AED,而不能得
出△ABC∽△ADE,故C不能判断△ABC∽ADE;
当 时,结合∠BAC=∠DAE,可证得△ABC∽△ADE,故D能判断△ABC∽△ADE;
故答案为:C
【分析】根据三角形相似的判定定理进行判断即可得到答案。
3. C
解:图中三角形有:△AEG,△ADC,CFG,△CBA,
∵AB∥EF∥DC,AD∥BC
∴△AEG∽△ADC∽CFG∽△CBA
共有6个组合分别为:∴△AEG∽△ADC,△AEG∽CFG,△AEG∽△CBA,△ADC∽CFG,△ADC∽△CBA,CFG∽△CBA。21·cn·jy·com
故答案为:C。
【分析】根据平行于三角形一边的直线截其它两边或两边的延长线,所截的三角形与原三角形相似得出△AEG∽△ADC∽CFG∽△CBA,从而即可得出答案。21*cnjy*com
4. A
∵AD=2BD,DE∥BC,
∴ .
∵ EF∥AB,
∴ . 【分析】根据平行线分线段成比例定理求解。
二、填空题
5. ∠ADE=∠C
解:添加∠ADE=∠C.
理由如下:
∵∠ADE=∠C,∠A=∠A,
∴△ADE∽△ACB.
故答案为:∠ADE=∠C(答案不唯一). 【分析】观察图形可知△ADE和△ACB有一个公共角,所以若使△ADE∽△ACB.再添加∠ADE=∠C或∠AED=∠B或AD:AE=AC:AB等条件都可。【出处:21教育名师】
6. 4或9
解:当△ADP∽△ACB时,需有 ,∴ ,解得AP=9.当△ADP∽△ABC时,需有 ,∴ ,解得AP=4.∴当AP的长为4或9时,△ADP和△ABC相似. 故答案为: 4或9 . 【分析】此题需要分类讨论:①当△ADP∽△ACB时,需有 , 根据比例式就可算出AP的长;②当△ADP∽△ABC时,需有 , 根据比例式就可算出AP的长,综上所述即可得出答案.
7. ③④⑤
解:②△CDB中CD:BC:BD=1:? ?:2 ?;
③△DEB中DE:BD:BE=2: ?: ?=1: ?: ?;
④△FBG中,FB:FG:BG= ?: ?:5=1: ?: ?;
⑤△HGF中,HG:HF:FG= ?:2: ?=1: ?: ?;
⑥△EKF中,KE:EF:FK= ?: ?:3.
其它两个三角形的三边之比不符合,故与①相似的三角形的序号是③④⑤.
故答案为:③④⑤
【分析】利用勾股定理可求出△ABC的三边之比为:1: ?: ?;再利用勾股定理分别求出△CDB,△DEB,△FBG,△HGF,△EKF的三边之比,从而可得到与△ABC相似的三角形的序号。21cnjy.com
8. ∠B=∠E(答案不唯一)
解:∵ = , ∠B=∠E ∴ △ABC ∽△ADE 故答案为:∠B=∠E www-2-1-cnjy-com
【分析】根据已知条件,两边对应成比例,因此添加这两边的夹角相等即可证得△ABC ∽△ADE。
9.
解:∵AB∥CD∥EF ∴BC:BE=AD:DF=1:3 即BC:(10-BC)=1:3 ∴BC=7.5 ∴CE=BE-BC=10-7.5=2.5。 【分析】根据平行线分线段成比例定理列出比例方程求出BC的长,进而可求得CE的长。
三、综合题
10. (1)2t;16﹣3t (2)解:∵∠PAQ=∠BAC,
∴当 时,△APQ∽△ABC,即 ,解得
当 时,△APQ∽△ACB,即 ,解得t=4.
∴运动时间为 秒或4秒.
(1)由题意得:AP=2t;AQ=AC-CQ=16-3t。 【分析】(1)由题意根据AP=时间×速度、AQ=AC-CQ(CQ=时间×速度)可求解; (2)由题意可分两种情况讨论求解: ①当可得关于t的方程,解方程即可求解; ②当可得关于t的方程,解方程即可求解;综合两种情况即可求解.【来源:21·世纪·教育·网】
一、单选题
1.下列4×4的正方形网格中,小正方形的边长均为1,三角形的顶点都在格点上,则与△ABC相似的三角形所在的网格图形是(?? ) 21世纪教育网版权所有
A.???????????????????B.???????????????????C.???????????????????D.?
2.如图,BE、CD相交于点A , 连接BC , DE , 下列条件中不能判断△ABC∽ADE的是(?? )
A.?∠B=∠D???????????????????????B.?∠C=∠E???????????????????????C.????????????????????????D.?
3.如图,AB∥EF∥DC,AD∥BC,EF与AC交于点G,则是相似三角形共有(?? )
A.?3对???????????????????????????????????????B.?5对???????????????????????????????????????C.?6对???????????????????????????????????????D.?8对
4.如图,在△ABC中,点D,E,F分别在边AB,AC,BC上,且DE∥BC,EF∥A
B.若AD=2BD,则 的值为(? )
A.???????????????????????????????????????????B.???????????????????????????????????????????C.???????????????????????????????????????????D.?
二、填空题
5.如图,添加一个条件:________,使△ADE∽△ACB.
6.如图,已知△ABC中,D为边AC上一点,P为边AB上一点,AB=12,AC=8,AD=6,当AP的长度为________时,△ADP和△ABC相似. www.21-cn-jy.com
7.如图,在正方形网格上有6个斜三角形:
①△ABC,②△CDB,③△DEB,④△FBG,⑤△HGF,⑥△EKF.
在②~⑥中,与①相似的三角形的序号是________.(把你认为正确的都填上)
8.如图,在△ABC和△ADE中, = ,要使△ABC 和 △ADE相似,还需要添加一个条件,这个条件是________ 21教育网
9.如图,AB∥CD∥EF,直线l1、l2与这三条平行线分别交于点A、D、F和点B、C、E.若AD:DF=3:1,BE=10,则CE的长为________。 2·1·c·n·j·y
三、综合题
10.如图,△ABC中,AB=8厘米,AC=16厘米,点P从A出发,以每秒2厘米的速度向B运动,点Q从C同时出发,以每秒3厘米的速度向A运动,其中一个动点到端点时,另一个动点也相应停止运动,设运动的时间为t. 21·世纪*教育网
(1)用含t的代数式表示:AP=________,AQ=________.
(2)当以A,P,Q为顶点的三角形与△ABC相似时,求运动时间是多少?
答案解析部分
一、单选题
1. C
解:根据勾股定理,AC= ,
所以,夹直角的两边的比为 =2,
观各选项,只有C选项三角形符合,与所给图形的三角形相似.
故答案为:C .
【分析】先求出两条直角边AC、BC的长度,进而求出其比值,然后利用”两边对应成比例且夹角相等的两个三角形相似”作出判断。2-1-c-n-j-y
2. C
解:∵∠BAC=∠DAE,
∴当∠B=∠D或∠C=∠E时,可利用两角对应相等的两个三角形相似证得△ABC∽ADE,故A、B选项可判断两三角形相似;【来源:21cnj*y.co*m】
当 时,可得 ,结合∠BAC=∠DAE,则可证得△ABC∽△AED,而不能得
出△ABC∽△ADE,故C不能判断△ABC∽ADE;
当 时,结合∠BAC=∠DAE,可证得△ABC∽△ADE,故D能判断△ABC∽△ADE;
故答案为:C
【分析】根据三角形相似的判定定理进行判断即可得到答案。
3. C
解:图中三角形有:△AEG,△ADC,CFG,△CBA,
∵AB∥EF∥DC,AD∥BC
∴△AEG∽△ADC∽CFG∽△CBA
共有6个组合分别为:∴△AEG∽△ADC,△AEG∽CFG,△AEG∽△CBA,△ADC∽CFG,△ADC∽△CBA,CFG∽△CBA。21·cn·jy·com
故答案为:C。
【分析】根据平行于三角形一边的直线截其它两边或两边的延长线,所截的三角形与原三角形相似得出△AEG∽△ADC∽CFG∽△CBA,从而即可得出答案。21*cnjy*com
4. A
∵AD=2BD,DE∥BC,
∴ .
∵ EF∥AB,
∴ . 【分析】根据平行线分线段成比例定理求解。
二、填空题
5. ∠ADE=∠C
解:添加∠ADE=∠C.
理由如下:
∵∠ADE=∠C,∠A=∠A,
∴△ADE∽△ACB.
故答案为:∠ADE=∠C(答案不唯一). 【分析】观察图形可知△ADE和△ACB有一个公共角,所以若使△ADE∽△ACB.再添加∠ADE=∠C或∠AED=∠B或AD:AE=AC:AB等条件都可。【出处:21教育名师】
6. 4或9
解:当△ADP∽△ACB时,需有 ,∴ ,解得AP=9.当△ADP∽△ABC时,需有 ,∴ ,解得AP=4.∴当AP的长为4或9时,△ADP和△ABC相似. 故答案为: 4或9 . 【分析】此题需要分类讨论:①当△ADP∽△ACB时,需有 , 根据比例式就可算出AP的长;②当△ADP∽△ABC时,需有 , 根据比例式就可算出AP的长,综上所述即可得出答案.
7. ③④⑤
解:②△CDB中CD:BC:BD=1:? ?:2 ?;
③△DEB中DE:BD:BE=2: ?: ?=1: ?: ?;
④△FBG中,FB:FG:BG= ?: ?:5=1: ?: ?;
⑤△HGF中,HG:HF:FG= ?:2: ?=1: ?: ?;
⑥△EKF中,KE:EF:FK= ?: ?:3.
其它两个三角形的三边之比不符合,故与①相似的三角形的序号是③④⑤.
故答案为:③④⑤
【分析】利用勾股定理可求出△ABC的三边之比为:1: ?: ?;再利用勾股定理分别求出△CDB,△DEB,△FBG,△HGF,△EKF的三边之比,从而可得到与△ABC相似的三角形的序号。21cnjy.com
8. ∠B=∠E(答案不唯一)
解:∵ = , ∠B=∠E ∴ △ABC ∽△ADE 故答案为:∠B=∠E www-2-1-cnjy-com
【分析】根据已知条件,两边对应成比例,因此添加这两边的夹角相等即可证得△ABC ∽△ADE。
9.
解:∵AB∥CD∥EF ∴BC:BE=AD:DF=1:3 即BC:(10-BC)=1:3 ∴BC=7.5 ∴CE=BE-BC=10-7.5=2.5。 【分析】根据平行线分线段成比例定理列出比例方程求出BC的长,进而可求得CE的长。
三、综合题
10. (1)2t;16﹣3t (2)解:∵∠PAQ=∠BAC,
∴当 时,△APQ∽△ABC,即 ,解得
当 时,△APQ∽△ACB,即 ,解得t=4.
∴运动时间为 秒或4秒.
(1)由题意得:AP=2t;AQ=AC-CQ=16-3t。 【分析】(1)由题意根据AP=时间×速度、AQ=AC-CQ(CQ=时间×速度)可求解; (2)由题意可分两种情况讨论求解: ①当可得关于t的方程,解方程即可求解; ②当可得关于t的方程,解方程即可求解;综合两种情况即可求解.【来源:21·世纪·教育·网】
