沪科版八年级数学上册第14章 全等三角形14.2.4 其他判定两个三角形全等的条件4课件(共19张)
文档属性
| 名称 | 沪科版八年级数学上册第14章 全等三角形14.2.4 其他判定两个三角形全等的条件4课件(共19张) |  | |
| 格式 | zip | ||
| 文件大小 | 501.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-01 10:12:11 | ||
图片预览





文档简介
(共19张PPT)
14.2 三角形全等的判定
第14章 全等三角形
第4课时 其他判定两个三角形全等的条件
1、如图,要证明△ACE≌ △BDF,根据给定的条件和指明的依据,将应当添设的条件填在横线上.
(1)AC∥BD,CE=DF,___.(SAS)
(2) AC=BD, AC∥BD ,__________. (ASA)
(3) CE= DF, , . (SSS)
AC=BD
∠A=∠B
AC=BD
AE=BF
一、复习回顾:
二、问题导入:
1、刚才我们应用了那些证明三角形全等的方法?
2、到目前为止我们已经学习了那些判断三角形全等的方法?
3、还有没有其它的判定方法呢?
三 、讲授新课:
给出三个条件画三角形时,共有六种情况,我们已经研究了三种:( )每种情况下作出的三角形都全等,剩下三种情况画出的三角形是否全等?
(4)三角相等;
(5)两边和其中一边的对角对应相等;
(6)两角和其中一角的对边对应相等.
SAS 、ASA 、 SSS
----- 利用 AA S判定三角形全等
A
B
C
A′
B′
C′
探究活动1:AAA 能否判定两个三角形全等
结论:三个内角对应相等的三角形不一定全等.
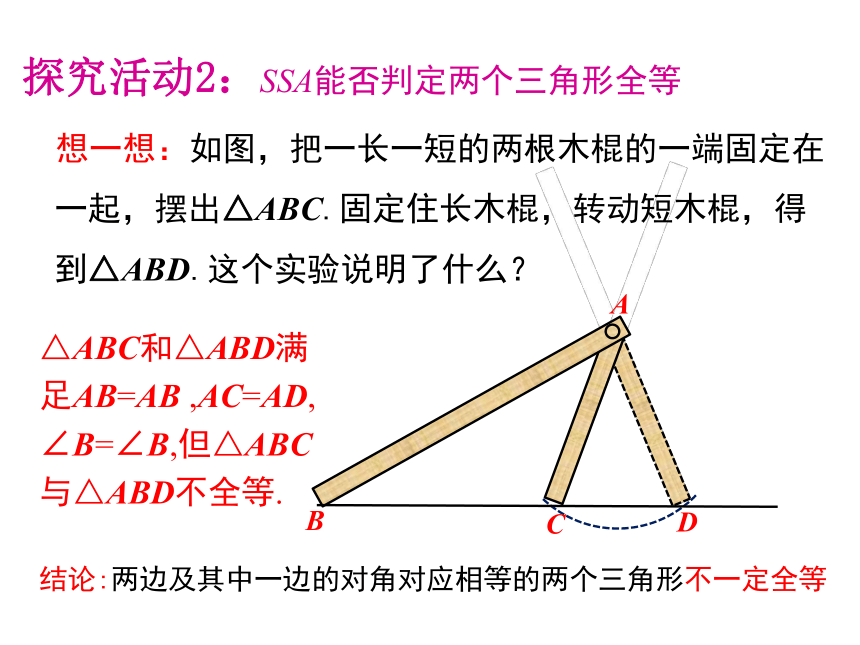
想一想:如图,把一长一短的两根木棍的一端固定在一起,摆出△ABC.固定住长木棍,转动短木棍,得到△ABD.这个实验说明了什么?
B
A
C
D
△ABC和△ABD满足AB=AB ,AC=AD,
∠B=∠B,但△ABC与△ABD不全等.
探究活动2:SSA能否判定两个三角形全等
结论:两边及其中一边的对角对应相等的两个三角形不一定全等
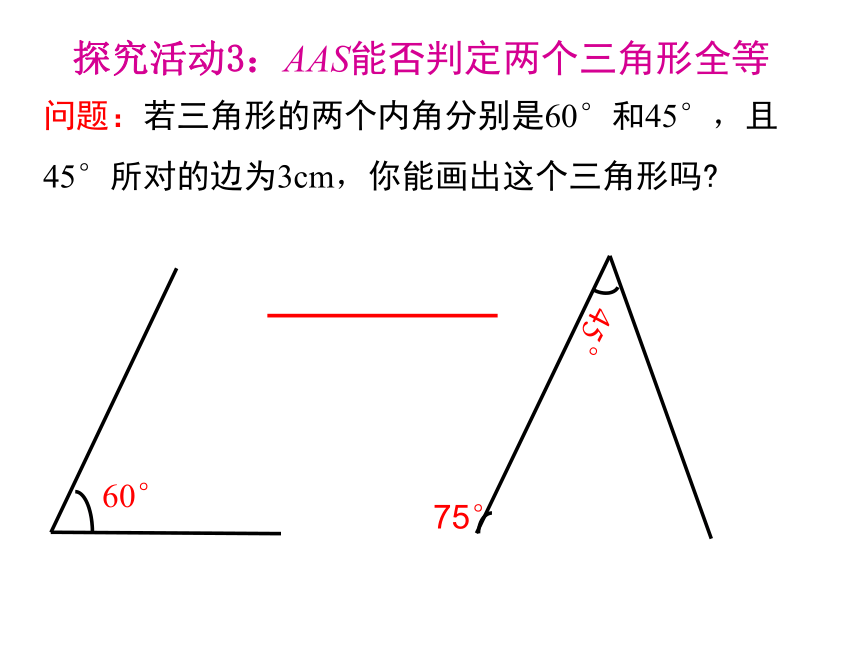
问题:若三角形的两个内角分别是60°和45°,且45°所对的边为3cm,你能画出这个三角形吗?
探究活动3:AAS能否判定两个三角形全等
两角和其中一角的对边对应相等的两个三角形全等.
简写成“角角边”或“AAS”.
归纳总结:
在△ABC和△DEF中,∠A=∠D,∠B= ∠E,BC=EF.
求证:△ABC≌△DEF.
∠B=∠E,
BC=EF,
∠C=∠F.
证明:
在△ABC中,∠A+∠B+∠C=180°.
∴△ABC≌△DEF(ASA ).
∴ ∠C=180°-∠A-∠B.
同理 ∠F=180°-∠D-∠E.
又 ∠A=∠D,∠B= ∠E,
∴ ∠C=∠F.
在△ABC和△DEF中,
“角角边”或“AAS”定理的证明
例1 如图,点B、F、C、D在同一条直线上,AB=ED,
AB∥ED,AC∥EF.求证:△ABC≌△EDF;BF=CD.
证明:∵ AB∥ED,AC∥EF(已知),
∴∠B=∠D,∠ACB=∠EFD.
(两直线平行,内错角相等)
在△ABC和△EDF中,
∠B=∠D(已证),
∠ACB=∠EFD(已证),
AB=ED(已知),
∴ △ABC≌△EDF(AAS)
∴BC=DF,∴BF=CD.
四、典例精析:
例2:如图,点B、F、C、D在同一条直线上,AB=ED,AB∥ED,AC∥EF.求证:BF=CD.
证明:∵ AB∥ED,AC∥EF(已知),
∴∠B=∠D,∠ACB=∠EFD.
(两直线平行,内错角相等)
在△ABC和△EDF中,
∠B=∠D(已证),
∠ACB=∠EFD(已证),
∵
AB=ED(已知),
∴ △ABC≌△EDF(AAS),∴BC=DF,∴BF=CD.
例3 如图,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.求证:(1)△BDA≌△AEC;
证明:(1)∵BD⊥m,CE⊥m,∴∠ADB=∠CEA=90°,
∴∠ABD+∠BAD=90°.
∵AB⊥AC,
∴∠BAD+∠CAE=90°,
∠ABD=∠CAE.
在△BDA和△AEC中,
∠ADB=∠CEA=90°,
∠ABD=∠CAE,
AB=AC,
∴△BDA≌△AEC(AAS).
(2)DE=BD+CE.
∴BD=AE,AD=CE,
∴DE=DA+AE=BD+CE.
证明:∵△BDA≌△AEC,
方法总结:利用全等三角形可以解决线段之间的关系,比如线段的相等关系、和差关系等,解决问题的关键是运用全等三角形的判定与性质进行线段之间的转化.
五、试试看:
1.如图,填空,使△AOC≌△BOD.
∠A=∠B(已知)
∠C=∠D(已知)
CO=DO或AO=BO
∴△AOC≌△BOD( AAS ).
2.如图,∠ABC=∠DCB,试添加一个条件,使得△ABC≌△DCB,这个条件可以是
(ASA)
或 (AAS)
或 (SAS)
∠ACB=∠DBC
∠A=∠D
AB=DC
A
B
C
D
E
F
3.如图∠ACB=∠DFE,BC=EF,那么应补充一个条件 ,才能使△ABC≌△DEF (写出一个即可).
∠B=∠E
或∠A=∠D
或 AC=DF
(ASA)
(AAS)
(SAS)
AB=DE可以吗?
×
AB∥DE
4.已知:如图, AB⊥BC,AD⊥DC,∠1=∠2, 求证:AB=AD.
证明: ∵ AB⊥BC,AD⊥DC,
∴ ∠ B=∠D=90 °.
在△ABC和△ADC中,
∴ △ABC≌△ADC(AAS),
∴AB=AD.
其他判定两个三角形全等的条件
三角形全等的“AAS”判定:两角分别相等且其中一组等角的对边相等的两个三角形全等
六、课堂小结:
“AAA”“SSA”不能作为两三角形全等判定依据
见《基础训练》本课时练习
七、课后作业:
14.2 三角形全等的判定
第14章 全等三角形
第4课时 其他判定两个三角形全等的条件
1、如图,要证明△ACE≌ △BDF,根据给定的条件和指明的依据,将应当添设的条件填在横线上.
(1)AC∥BD,CE=DF,___.(SAS)
(2) AC=BD, AC∥BD ,__________. (ASA)
(3) CE= DF, , . (SSS)
AC=BD
∠A=∠B
AC=BD
AE=BF
一、复习回顾:
二、问题导入:
1、刚才我们应用了那些证明三角形全等的方法?
2、到目前为止我们已经学习了那些判断三角形全等的方法?
3、还有没有其它的判定方法呢?
三 、讲授新课:
给出三个条件画三角形时,共有六种情况,我们已经研究了三种:( )每种情况下作出的三角形都全等,剩下三种情况画出的三角形是否全等?
(4)三角相等;
(5)两边和其中一边的对角对应相等;
(6)两角和其中一角的对边对应相等.
SAS 、ASA 、 SSS
----- 利用 AA S判定三角形全等
A
B
C
A′
B′
C′
探究活动1:AAA 能否判定两个三角形全等
结论:三个内角对应相等的三角形不一定全等.
想一想:如图,把一长一短的两根木棍的一端固定在一起,摆出△ABC.固定住长木棍,转动短木棍,得到△ABD.这个实验说明了什么?
B
A
C
D
△ABC和△ABD满足AB=AB ,AC=AD,
∠B=∠B,但△ABC与△ABD不全等.
探究活动2:SSA能否判定两个三角形全等
结论:两边及其中一边的对角对应相等的两个三角形不一定全等
问题:若三角形的两个内角分别是60°和45°,且45°所对的边为3cm,你能画出这个三角形吗?
探究活动3:AAS能否判定两个三角形全等
两角和其中一角的对边对应相等的两个三角形全等.
简写成“角角边”或“AAS”.
归纳总结:
在△ABC和△DEF中,∠A=∠D,∠B= ∠E,BC=EF.
求证:△ABC≌△DEF.
∠B=∠E,
BC=EF,
∠C=∠F.
证明:
在△ABC中,∠A+∠B+∠C=180°.
∴△ABC≌△DEF(ASA ).
∴ ∠C=180°-∠A-∠B.
同理 ∠F=180°-∠D-∠E.
又 ∠A=∠D,∠B= ∠E,
∴ ∠C=∠F.
在△ABC和△DEF中,
“角角边”或“AAS”定理的证明
例1 如图,点B、F、C、D在同一条直线上,AB=ED,
AB∥ED,AC∥EF.求证:△ABC≌△EDF;BF=CD.
证明:∵ AB∥ED,AC∥EF(已知),
∴∠B=∠D,∠ACB=∠EFD.
(两直线平行,内错角相等)
在△ABC和△EDF中,
∠B=∠D(已证),
∠ACB=∠EFD(已证),
AB=ED(已知),
∴ △ABC≌△EDF(AAS)
∴BC=DF,∴BF=CD.
四、典例精析:
例2:如图,点B、F、C、D在同一条直线上,AB=ED,AB∥ED,AC∥EF.求证:BF=CD.
证明:∵ AB∥ED,AC∥EF(已知),
∴∠B=∠D,∠ACB=∠EFD.
(两直线平行,内错角相等)
在△ABC和△EDF中,
∠B=∠D(已证),
∠ACB=∠EFD(已证),
∵
AB=ED(已知),
∴ △ABC≌△EDF(AAS),∴BC=DF,∴BF=CD.
例3 如图,已知:在△ABC中,∠BAC=90°,AB=AC,直线m经过点A,BD⊥直线m,CE⊥直线m,垂足分别为点D、E.求证:(1)△BDA≌△AEC;
证明:(1)∵BD⊥m,CE⊥m,∴∠ADB=∠CEA=90°,
∴∠ABD+∠BAD=90°.
∵AB⊥AC,
∴∠BAD+∠CAE=90°,
∠ABD=∠CAE.
在△BDA和△AEC中,
∠ADB=∠CEA=90°,
∠ABD=∠CAE,
AB=AC,
∴△BDA≌△AEC(AAS).
(2)DE=BD+CE.
∴BD=AE,AD=CE,
∴DE=DA+AE=BD+CE.
证明:∵△BDA≌△AEC,
方法总结:利用全等三角形可以解决线段之间的关系,比如线段的相等关系、和差关系等,解决问题的关键是运用全等三角形的判定与性质进行线段之间的转化.
五、试试看:
1.如图,填空,使△AOC≌△BOD.
∠A=∠B(已知)
∠C=∠D(已知)
CO=DO或AO=BO
∴△AOC≌△BOD( AAS ).
2.如图,∠ABC=∠DCB,试添加一个条件,使得△ABC≌△DCB,这个条件可以是
(ASA)
或 (AAS)
或 (SAS)
∠ACB=∠DBC
∠A=∠D
AB=DC
A
B
C
D
E
F
3.如图∠ACB=∠DFE,BC=EF,那么应补充一个条件 ,才能使△ABC≌△DEF (写出一个即可).
∠B=∠E
或∠A=∠D
或 AC=DF
(ASA)
(AAS)
(SAS)
AB=DE可以吗?
×
AB∥DE
4.已知:如图, AB⊥BC,AD⊥DC,∠1=∠2, 求证:AB=AD.
证明: ∵ AB⊥BC,AD⊥DC,
∴ ∠ B=∠D=90 °.
在△ABC和△ADC中,
∴ △ABC≌△ADC(AAS),
∴AB=AD.
其他判定两个三角形全等的条件
三角形全等的“AAS”判定:两角分别相等且其中一组等角的对边相等的两个三角形全等
六、课堂小结:
“AAA”“SSA”不能作为两三角形全等判定依据
见《基础训练》本课时练习
七、课后作业:
