人教版数学必修1 3.1.1 方程的根与函数的零点(共17张ppt)
文档属性
| 名称 | 人教版数学必修1 3.1.1 方程的根与函数的零点(共17张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 282.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-03 00:00:00 | ||
图片预览



文档简介
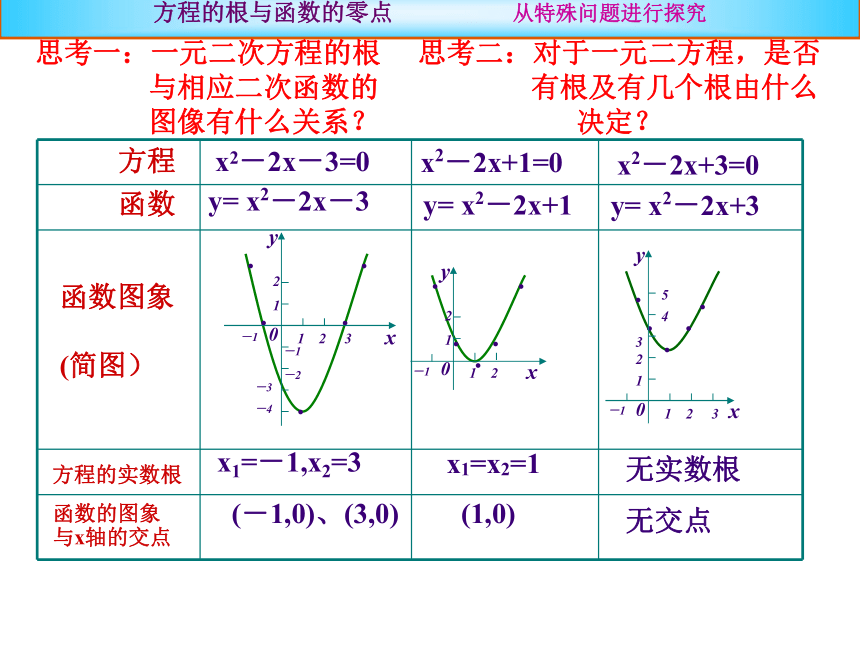
课件17张PPT。求下列方程的根发现问题:方程x2-2x+1=0x2-2x+3=0y= x2-2x-3y= x2-2x+1函数函数图象
(简图)方程的实数根x1=-1,x2=3x1=x2=1无实数根(-1,0)、(3,0)(1,0)无交点x2-2x-3=0y= x2-2x+3
函数的图象
与x轴的交点方程的根与函数的零点 从特殊问题进行探究 思考二:对于一元二方程,是否
有根及有几个根由什么
决定?思考一:一元二次方程的根
与相应二次函数的
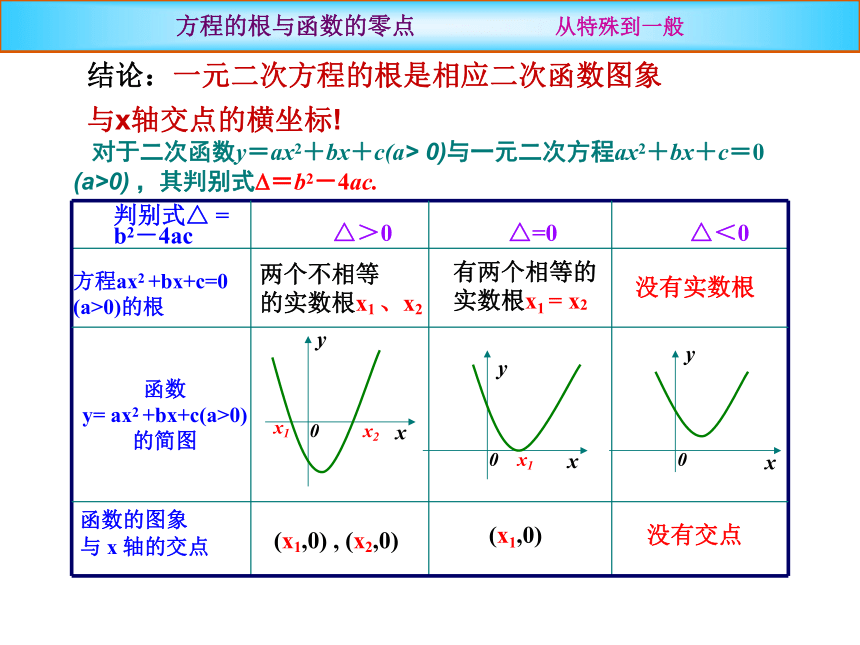
图像有什么关系?方程ax2 +bx+c=0
(a>0)的根函数
y= ax2 +bx+c(a>0) 的简图
判别式△ =
b2-4ac△>0△=0△<0函数的图象
与 x 轴的交点有两个相等的
实数根x1 = x2没有实数根(x1,0) , (x2,0)(x1,0)没有交点两个不相等
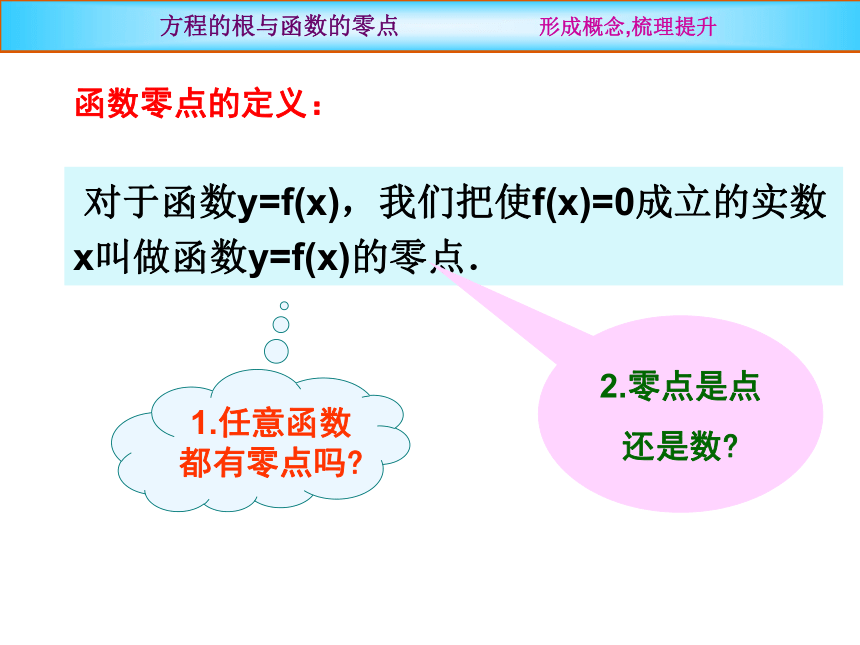
的实数根x1 、x2对于二次函数y=ax2+bx+c(a> 0)与一元二次方程ax2+bx+c=0 (a>0) ,其判别式?=b2-4ac.方程的根与函数的零点 从特殊到一般 结论:一元二次方程的根是相应二次函数图象 与x轴交点的横坐标! 对于函数y=f(x),我们把使f(x)=0成立的实数x叫做函数y=f(x)的零点.方程的根与函数的零点 形成概念,梳理提升函数零点的定义:2.零点是点还是数?1.任意函数都有零点吗?方程f(x) =0
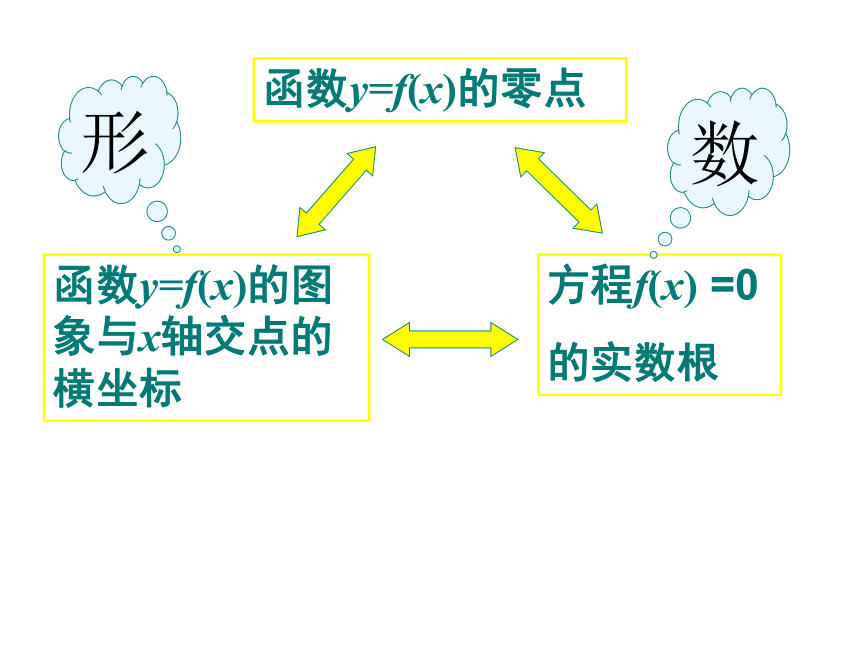
的实数根函数y=f(x)的图象与x轴交点的横坐标函数y=f(x)的零点形数求下列函数的零点:练习: 进一步研究函数 f(x)=x2-2x-3图像
3问题探究:函数零点存在性定理: 如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a)·f(b)<0,那么,函数y=f(x)在区间(a,b) 内有零点。即存在 c∈(a,b) ,使得 f(c) =0, 这个c也就是方程 f(x)=0 的根。1、连续函数y=f(x)在区间(a,b)内有零点,
则f(a)·f(b)<0。
2、连续函数y=f(x),若f(a)·f(b)<0,则函数
y=f(x)在区间(a,b)内只有一个零点。合作探究以下两个问题是否成立? 一般地,若函数y=f(x)在区间
[a,b]上的图象是一条单调并连续的
曲线,且f(a)·f(b)<0,则函数y=f(x)在区间(a,b)上有唯一零点.零点存在性的一种模型例 :已知函数 结合下表确定它
有几个零点及零点所在区间典例研究:由表可知,f(2)<0,
f(3)>0,f(2)f(3)<0,这说明
函数f(x)在区间(2,3)内有零点。思考:如何判定零点的 个数?
因为函数f(x)在(0,+∞)
内单调递增所以它仅有一
个零点.课堂检测:课堂检测:函数的零点定义零点的求解及所在区间的判断 小 结函数零点存在性定理课本88页1、2作业求函数的零点个数,并指出其零点所在的大致区间。
(简图)方程的实数根x1=-1,x2=3x1=x2=1无实数根(-1,0)、(3,0)(1,0)无交点x2-2x-3=0y= x2-2x+3
函数的图象
与x轴的交点方程的根与函数的零点 从特殊问题进行探究 思考二:对于一元二方程,是否
有根及有几个根由什么
决定?思考一:一元二次方程的根
与相应二次函数的
图像有什么关系?方程ax2 +bx+c=0
(a>0)的根函数
y= ax2 +bx+c(a>0) 的简图
判别式△ =
b2-4ac△>0△=0△<0函数的图象
与 x 轴的交点有两个相等的
实数根x1 = x2没有实数根(x1,0) , (x2,0)(x1,0)没有交点两个不相等
的实数根x1 、x2对于二次函数y=ax2+bx+c(a> 0)与一元二次方程ax2+bx+c=0 (a>0) ,其判别式?=b2-4ac.方程的根与函数的零点 从特殊到一般 结论:一元二次方程的根是相应二次函数图象 与x轴交点的横坐标! 对于函数y=f(x),我们把使f(x)=0成立的实数x叫做函数y=f(x)的零点.方程的根与函数的零点 形成概念,梳理提升函数零点的定义:2.零点是点还是数?1.任意函数都有零点吗?方程f(x) =0
的实数根函数y=f(x)的图象与x轴交点的横坐标函数y=f(x)的零点形数求下列函数的零点:练习: 进一步研究函数 f(x)=x2-2x-3图像
3问题探究:函数零点存在性定理: 如果函数y=f(x)在区间[a,b]上的图象是连续不断的一条曲线,并且有f(a)·f(b)<0,那么,函数y=f(x)在区间(a,b) 内有零点。即存在 c∈(a,b) ,使得 f(c) =0, 这个c也就是方程 f(x)=0 的根。1、连续函数y=f(x)在区间(a,b)内有零点,
则f(a)·f(b)<0。
2、连续函数y=f(x),若f(a)·f(b)<0,则函数
y=f(x)在区间(a,b)内只有一个零点。合作探究以下两个问题是否成立? 一般地,若函数y=f(x)在区间
[a,b]上的图象是一条单调并连续的
曲线,且f(a)·f(b)<0,则函数y=f(x)在区间(a,b)上有唯一零点.零点存在性的一种模型例 :已知函数 结合下表确定它
有几个零点及零点所在区间典例研究:由表可知,f(2)<0,
f(3)>0,f(2)f(3)<0,这说明
函数f(x)在区间(2,3)内有零点。思考:如何判定零点的 个数?
因为函数f(x)在(0,+∞)
内单调递增所以它仅有一
个零点.课堂检测:课堂检测:函数的零点定义零点的求解及所在区间的判断 小 结函数零点存在性定理课本88页1、2作业求函数的零点个数,并指出其零点所在的大致区间。
