人教版八年级数学下册19.1.2函数的图象第2课时函数的表示方法同步练习含答案
文档属性
| 名称 | 人教版八年级数学下册19.1.2函数的图象第2课时函数的表示方法同步练习含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 396.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-30 20:31:56 | ||
图片预览

文档简介
19.1.2 函数的图象
第2课时 函数的表示方法
选择题
1.父亲告诉小明:“距离地面越高,温度越低”,并且出示了下面的表格:
距离地面高度(千米)
0
1
2
3
4
5
温度(℃)
20
14
8
2
﹣4
﹣10
那么根据表格中的规律,距离地面6千米的高空温度是( )
A.
﹣10℃
B.
﹣16℃
C.
﹣18℃
D.
﹣20℃
2.如图,△ABC中,已知BC=16,高AD=10,动点C′由点C沿CB向点B移动(不与点B重合).设CC′的长为x,△ABC′的面积为S,则S与x之间的函数关系式为( )
A.
S=80﹣5x
B.
S=5x
C.
S=10x
D.
S=5x+80
3.下表是弹簧挂重后的总长度L(cm)与所挂物体重量x(kg)之间的几个对应值,则可以推测L与x之间的关系式是( )
所挂重量x(kg)
0
0.5
1
1.5
2
弹簧总长度L(cm)
20
21
22
23
24
A.
L=2x
B.
L=2x+20
C.
L=x+20
D.
L=x
4.一名老师带领x名学生到动物园参观,已知成人票每张30元,学生票每张10元.设门票的总费用为y元,则y与x的函数关系为( )
A.
y=10x+30
B.
y=40x
C.
y=10+30x
D.
y=20x
5.弹簧挂上物体后会伸长,已知一弹簧的长度(cm)与所挂物体的质量(kg)之间的关系如表,由上表可知下列说法错误的是( )
物体的质量(kg)
0
1
2
3
4
5
弹簧的长度(cm)
12
12.5
13
13.5
14
14.5
A.
弹簧的长度随物体质量的变化而变化,其中物体的质量是自变量,弹簧的长度是因变量
B.
如果物体的质量为4kg,那么弹簧的长度为14cm
C.
在弹簧能承受的范围内,当物体的质量为6kg时,弹簧的长度为16cm
D.
在没挂物体时,弹簧的长度为12cm
6.若y与x的关系式为y=30x﹣6,当x=时,y的值为( )
A.
5
B.
10
C.
4
D.
﹣4
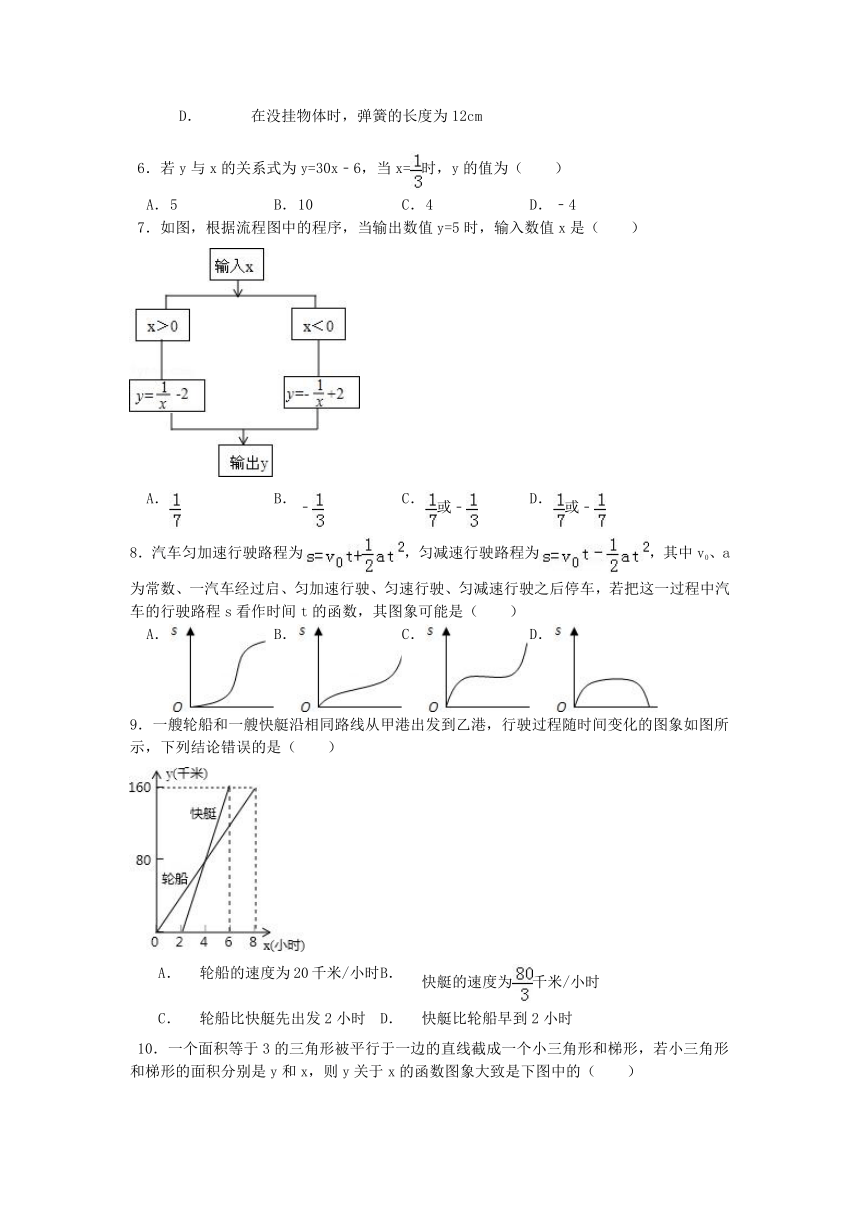
7.如图,根据流程图中的程序,当输出数值y=5时,输入数值x是( )
A.
B.
﹣
C.
或﹣
D.
或﹣
8.汽车匀加速行驶路程为,匀减速行驶路程为,其中v0、a为常数、一汽车经过启、匀加速行驶、匀速行驶、匀减速行驶之后停车,若把这一过程中汽车的行驶路程s看作时间t的函数,其图象可能是( )
A.
B.
C.
D.
9.一艘轮船和一艘快艇沿相同路线从甲港出发到乙港,行驶过程随时间变化的图象如图所示,下列结论错误的是( )
A.
轮船的速度为20千米/小时
B.
快艇的速度为千米/小时
C.
轮船比快艇先出发2小时
D.
快艇比轮船早到2小时
10.一个面积等于3的三角形被平行于一边的直线截成一个小三角形和梯形,若小三角形和梯形的面积分别是y和x,则y关于x的函数图象大致是下图中的( )
A.
B.
C.
D.
11.如图所示,一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.下列说法中正确的是( )
A.
B点表示此时快车到达乙地
B.
B﹣C﹣D段表示慢车先加速后减速最后到达甲地
C.
快车的速度为km/h
D.
慢车的速度为125km/h
二.填空题
12.函数的自变量x的取值范围是 .
13.写出一个函数,使得满足下列两个条件:
①经过点(﹣1,1);②在x>0时,y随x的增大而增大.
你写出的函数是 .
14.油箱中有油30kg,油从管道中匀速流出,1h流完,则油箱中剩余油量Q(kg)与流出时间t(min)之间的函数关系式是 ;自变量x的取值范围是 .
15.一慢车和一快车沿相同路线从A地到B地,所行的路程与时间的图象如图,则慢车比快车早出发 小时,快车追上慢车行驶了 千米,快车比慢车早 小时到达B地.
16.小明从家跑步到学校,接着马上原路步行回家.如图是小明离家的路程y(米)与时间t(分)的函数图象,则小明回家的速度是每分钟步行 米.
17.小明放学后步行回家,他离家的路程s(米)与步行时间t(分钟)的函数图象如图所示,则他步行回家的平均速度是 米/分钟.
18.在全民健身环城越野赛中,甲、乙两选手的行程y(千米)随时间(时)变化的图象(全程)如图所示.有下列说法:
①起跑后1小时内,甲在乙的前面;
②第1小时两人都跑了10千米;
③甲比乙先到达终点;
④两人都跑了20千米.
其中正确的说法的序号是 .
19.三军受命,我解放军各部奋力抗战在救灾一线.现有甲、乙两支解放军小分队将救灾物资送往某重灾小镇,甲队先出发,从部队基地到该小镇只有唯一通道,且路程为24km.如图是他们行走的路程关于时间的函数图象,四位同学观察此函数图象得出有关信息,其中正确的说法有 (填序号如①②③④).
20.甲、乙两人前往12千米外的地方植树.图中l甲、l乙分别表示甲、乙行驶的路程S(千米)与时间t(分)的函数关系,则每分钟乙比甲多走 千米.
一.选择题
1.B 2.A 3.B 4.A 5.C 6.C 7.C 8.A 9.B 10.A 11.C
二.填空题
12.x≠-3 13.y=x2 14.Q=30-0.5x0≤x≤60
15.22764 16.80 17.80 18.①②④ 19.①②③④ 20.
第2课时 函数的表示方法
选择题
1.父亲告诉小明:“距离地面越高,温度越低”,并且出示了下面的表格:
距离地面高度(千米)
0
1
2
3
4
5
温度(℃)
20
14
8
2
﹣4
﹣10
那么根据表格中的规律,距离地面6千米的高空温度是( )
A.
﹣10℃
B.
﹣16℃
C.
﹣18℃
D.
﹣20℃
2.如图,△ABC中,已知BC=16,高AD=10,动点C′由点C沿CB向点B移动(不与点B重合).设CC′的长为x,△ABC′的面积为S,则S与x之间的函数关系式为( )
A.
S=80﹣5x
B.
S=5x
C.
S=10x
D.
S=5x+80
3.下表是弹簧挂重后的总长度L(cm)与所挂物体重量x(kg)之间的几个对应值,则可以推测L与x之间的关系式是( )
所挂重量x(kg)
0
0.5
1
1.5
2
弹簧总长度L(cm)
20
21
22
23
24
A.
L=2x
B.
L=2x+20
C.
L=x+20
D.
L=x
4.一名老师带领x名学生到动物园参观,已知成人票每张30元,学生票每张10元.设门票的总费用为y元,则y与x的函数关系为( )
A.
y=10x+30
B.
y=40x
C.
y=10+30x
D.
y=20x
5.弹簧挂上物体后会伸长,已知一弹簧的长度(cm)与所挂物体的质量(kg)之间的关系如表,由上表可知下列说法错误的是( )
物体的质量(kg)
0
1
2
3
4
5
弹簧的长度(cm)
12
12.5
13
13.5
14
14.5
A.
弹簧的长度随物体质量的变化而变化,其中物体的质量是自变量,弹簧的长度是因变量
B.
如果物体的质量为4kg,那么弹簧的长度为14cm
C.
在弹簧能承受的范围内,当物体的质量为6kg时,弹簧的长度为16cm
D.
在没挂物体时,弹簧的长度为12cm
6.若y与x的关系式为y=30x﹣6,当x=时,y的值为( )
A.
5
B.
10
C.
4
D.
﹣4
7.如图,根据流程图中的程序,当输出数值y=5时,输入数值x是( )
A.
B.
﹣
C.
或﹣
D.
或﹣
8.汽车匀加速行驶路程为,匀减速行驶路程为,其中v0、a为常数、一汽车经过启、匀加速行驶、匀速行驶、匀减速行驶之后停车,若把这一过程中汽车的行驶路程s看作时间t的函数,其图象可能是( )
A.
B.
C.
D.
9.一艘轮船和一艘快艇沿相同路线从甲港出发到乙港,行驶过程随时间变化的图象如图所示,下列结论错误的是( )
A.
轮船的速度为20千米/小时
B.
快艇的速度为千米/小时
C.
轮船比快艇先出发2小时
D.
快艇比轮船早到2小时
10.一个面积等于3的三角形被平行于一边的直线截成一个小三角形和梯形,若小三角形和梯形的面积分别是y和x,则y关于x的函数图象大致是下图中的( )
A.
B.
C.
D.
11.如图所示,一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发,设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.下列说法中正确的是( )
A.
B点表示此时快车到达乙地
B.
B﹣C﹣D段表示慢车先加速后减速最后到达甲地
C.
快车的速度为km/h
D.
慢车的速度为125km/h
二.填空题
12.函数的自变量x的取值范围是 .
13.写出一个函数,使得满足下列两个条件:
①经过点(﹣1,1);②在x>0时,y随x的增大而增大.
你写出的函数是 .
14.油箱中有油30kg,油从管道中匀速流出,1h流完,则油箱中剩余油量Q(kg)与流出时间t(min)之间的函数关系式是 ;自变量x的取值范围是 .
15.一慢车和一快车沿相同路线从A地到B地,所行的路程与时间的图象如图,则慢车比快车早出发 小时,快车追上慢车行驶了 千米,快车比慢车早 小时到达B地.
16.小明从家跑步到学校,接着马上原路步行回家.如图是小明离家的路程y(米)与时间t(分)的函数图象,则小明回家的速度是每分钟步行 米.
17.小明放学后步行回家,他离家的路程s(米)与步行时间t(分钟)的函数图象如图所示,则他步行回家的平均速度是 米/分钟.
18.在全民健身环城越野赛中,甲、乙两选手的行程y(千米)随时间(时)变化的图象(全程)如图所示.有下列说法:
①起跑后1小时内,甲在乙的前面;
②第1小时两人都跑了10千米;
③甲比乙先到达终点;
④两人都跑了20千米.
其中正确的说法的序号是 .
19.三军受命,我解放军各部奋力抗战在救灾一线.现有甲、乙两支解放军小分队将救灾物资送往某重灾小镇,甲队先出发,从部队基地到该小镇只有唯一通道,且路程为24km.如图是他们行走的路程关于时间的函数图象,四位同学观察此函数图象得出有关信息,其中正确的说法有 (填序号如①②③④).
20.甲、乙两人前往12千米外的地方植树.图中l甲、l乙分别表示甲、乙行驶的路程S(千米)与时间t(分)的函数关系,则每分钟乙比甲多走 千米.
一.选择题
1.B 2.A 3.B 4.A 5.C 6.C 7.C 8.A 9.B 10.A 11.C
二.填空题
12.x≠-3 13.y=x2 14.Q=30-0.5x0≤x≤60
15.22764 16.80 17.80 18.①②④ 19.①②③④ 20.
