14.2.1 两边及其夹角分别相等的两个三角形学案(要点讲解+当堂检测+答案)
文档属性
| 名称 | 14.2.1 两边及其夹角分别相等的两个三角形学案(要点讲解+当堂检测+答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-29 00:00:00 | ||
图片预览

文档简介
沪科版数学八年级上册同步学案
第14章 全等三角形
14.2 三角形全等的判定
14.2.1 两边及其夹角分别相等的两个三角形
要 点 讲 解
要点 运用“边角边”判定两个三角形全等及其简单应用
两边及其夹角分别相等的两个三角形全等,简记为“边角边”或“SAS”.
应用格式:如图,在△ABC和△DEF中,∵
(1)此方法包含“边”和“角”两种元素,必须是两边夹一角才行,而不是两边及一边对角分别相等,一定要注意元素的“对应”关系.
(2)此方法在应用时,可以从图形上直接观察到三个对应元素必须符合“两边夹角”,即“SAS”,不要错误认为有两边一角就能判定两个三角形全等.在书写时要按照“边→角→边”的顺序排列条件,必须牢记“边边角”不能作为判定两个三角形全等的条件.
经典例题 如图所示,已知E,F是线段AB上的两点,且AE=BF,AD=BC,∠A=∠B.求证:DF=CE.
解析:先证明AF=BE,再用“SAS”证明两个三角形全等.
证明:∵AE=BF(已知),
∴AE+EF=BF+FE(等式性质1),
即AF=BE.
在△DAF和△CBE中,∵
∴△DAF≌△CBE(SAS).∴DF=CE(全等三角形的对应边相等).
点拨:本题直接给出了一边一角分别相等,因此再证出另一边(即AF=BE)相等即可利用“SAS”证两个三角形全等,进而推出对应边相等.
当 堂 检 测
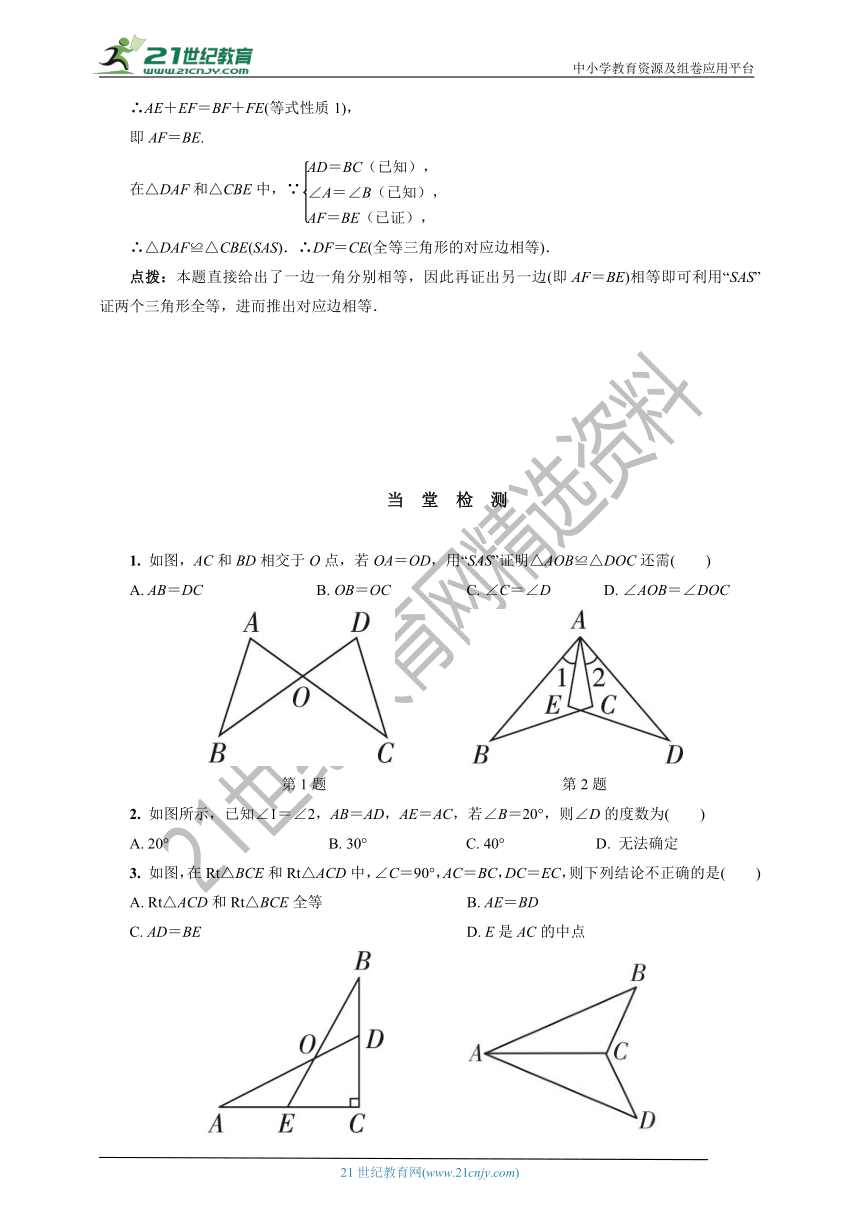
1. 如图,AC和BD相交于O点,若OA=OD,用“SAS”证明△AOB≌△DOC还需( )
A. AB=DC B. OB=OC C. ∠C=∠D D. ∠AOB=∠DOC
第1题 第2题
2. 如图所示,已知∠1=∠2,AB=AD,AE=AC,若∠B=20°,则∠D的度数为( )
A. 20° B. 30° C. 40° D. 无法确定
3. 如图,在Rt△BCE和Rt△ACD中,∠C=90°,AC=BC,DC=EC,则下列结论不正确的是( )
A. Rt△ACD和Rt△BCE全等 B. AE=BD
C. AD=BE D. E是AC的中点
第3题 第4题
4. 如图,要使△ABC≌△ADC,只要具备条件( )
A. AB=AD,∠B=∠D B. AB=AD,∠ACB=∠ACD
C. BC=DC,∠BAC=∠DAC D. AB=AD,∠BAC=∠DAC
5. 如图,点F,C在线段BE上,且∠1=∠2,BF=EC,若要使△ABC≌△DEF.则还必须补充一个条件 .
6. 如图,四边形ABCD的对角线AC,BD相交于点O,△ABO≌△ADO.下列结论:①AC⊥BD;②CB=CD;③△ABC≌△ADC;④DA=DC.其中所有正确结论的序号是 .
第6题 第7题
7. 把两根钢条AC,BD的中点连在一起,可以做成一个测量工件内槽宽的工具(卡钳),如图,若测得AB=5厘米,则槽宽CD为 米.
8. 如图,BE=CE,∠1=∠2,求证:△ABE≌△ACE.
9. 如图所示,有一池塘,要测池塘两端的两棵树A,B之间的距离,可先在平地上取一个可以直接到达A,B的点C.连接AC并延长到D,使CD=CA;再连接BC并延长到点E,使CE=CB,然后测出DE的长度就是两棵树A,B之间的距离,请你说明其中的道理.
当堂检测参考答案
1. B 2. A 3. D 4. D
5. AC=DF
6. ①②③
7. 0.05
8. 证明:∵∠AEB+∠1=180°,∠AEC+∠2=180°,∠1=∠2,∴∠AEB=∠AEC,在△ABE和△ACE中,∴△ABE≌△ACE(SAS).
9. 解:在△CED和△CBA中,∵ ∴△CED≌△CBA.∴DE=AB.
第14章 全等三角形
14.2 三角形全等的判定
14.2.1 两边及其夹角分别相等的两个三角形
要 点 讲 解
要点 运用“边角边”判定两个三角形全等及其简单应用
两边及其夹角分别相等的两个三角形全等,简记为“边角边”或“SAS”.
应用格式:如图,在△ABC和△DEF中,∵
(1)此方法包含“边”和“角”两种元素,必须是两边夹一角才行,而不是两边及一边对角分别相等,一定要注意元素的“对应”关系.
(2)此方法在应用时,可以从图形上直接观察到三个对应元素必须符合“两边夹角”,即“SAS”,不要错误认为有两边一角就能判定两个三角形全等.在书写时要按照“边→角→边”的顺序排列条件,必须牢记“边边角”不能作为判定两个三角形全等的条件.
经典例题 如图所示,已知E,F是线段AB上的两点,且AE=BF,AD=BC,∠A=∠B.求证:DF=CE.
解析:先证明AF=BE,再用“SAS”证明两个三角形全等.
证明:∵AE=BF(已知),
∴AE+EF=BF+FE(等式性质1),
即AF=BE.
在△DAF和△CBE中,∵
∴△DAF≌△CBE(SAS).∴DF=CE(全等三角形的对应边相等).
点拨:本题直接给出了一边一角分别相等,因此再证出另一边(即AF=BE)相等即可利用“SAS”证两个三角形全等,进而推出对应边相等.
当 堂 检 测
1. 如图,AC和BD相交于O点,若OA=OD,用“SAS”证明△AOB≌△DOC还需( )
A. AB=DC B. OB=OC C. ∠C=∠D D. ∠AOB=∠DOC
第1题 第2题
2. 如图所示,已知∠1=∠2,AB=AD,AE=AC,若∠B=20°,则∠D的度数为( )
A. 20° B. 30° C. 40° D. 无法确定
3. 如图,在Rt△BCE和Rt△ACD中,∠C=90°,AC=BC,DC=EC,则下列结论不正确的是( )
A. Rt△ACD和Rt△BCE全等 B. AE=BD
C. AD=BE D. E是AC的中点
第3题 第4题
4. 如图,要使△ABC≌△ADC,只要具备条件( )
A. AB=AD,∠B=∠D B. AB=AD,∠ACB=∠ACD
C. BC=DC,∠BAC=∠DAC D. AB=AD,∠BAC=∠DAC
5. 如图,点F,C在线段BE上,且∠1=∠2,BF=EC,若要使△ABC≌△DEF.则还必须补充一个条件 .
6. 如图,四边形ABCD的对角线AC,BD相交于点O,△ABO≌△ADO.下列结论:①AC⊥BD;②CB=CD;③△ABC≌△ADC;④DA=DC.其中所有正确结论的序号是 .
第6题 第7题
7. 把两根钢条AC,BD的中点连在一起,可以做成一个测量工件内槽宽的工具(卡钳),如图,若测得AB=5厘米,则槽宽CD为 米.
8. 如图,BE=CE,∠1=∠2,求证:△ABE≌△ACE.
9. 如图所示,有一池塘,要测池塘两端的两棵树A,B之间的距离,可先在平地上取一个可以直接到达A,B的点C.连接AC并延长到D,使CD=CA;再连接BC并延长到点E,使CE=CB,然后测出DE的长度就是两棵树A,B之间的距离,请你说明其中的道理.
当堂检测参考答案
1. B 2. A 3. D 4. D
5. AC=DF
6. ①②③
7. 0.05
8. 证明:∵∠AEB+∠1=180°,∠AEC+∠2=180°,∠1=∠2,∴∠AEB=∠AEC,在△ABE和△ACE中,∴△ABE≌△ACE(SAS).
9. 解:在△CED和△CBA中,∵ ∴△CED≌△CBA.∴DE=AB.
