2019-2020学年陕西省汉中市高二(上)期中数学试卷(文科)(PDF版 含答案)
文档属性
| 名称 | 2019-2020学年陕西省汉中市高二(上)期中数学试卷(文科)(PDF版 含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 334.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-03 22:21:38 | ||
图片预览



文档简介
- 1 -
2019-2020 学年陕西省汉中市高二(上)期中数学试卷(文科)
一、选择题:本大题共 12 小题,每小题 5 分,满分 60 分,在每小题给出的四个选项中,
只有一项是符合题目要求的.
1.已知集合 { 1A ? ? ,0,1}, { | 2 1}xB x? ? ,则 (A B ?? )
A.{ 1? ,0,1} B.{ 1? , 0} C.{0,1} D.{ 1? ,1}
2.命题“存在 x R? , 2 1 0x x? ? ? 的否定是 ( )
A.不存在 x R? , 2 1 0x x? ? ? B.存在 x R? , 2 2 0x x? ? ?
C.对任意的 x R? , 2 1 0x x? ? ? D.对任意的 x R? , 2 1 0x x? ? ?
3.小明出国旅游,当地时间比中国时间晚一个小时,他需要将表的时针旋转,则转过的角
的弧度数是 ( )
A.
3
? B.
6
? C.
3
?
? D.
6
?
?
4.平面向量 a?与 b
?
的夹角为 60?,且 (3,0)a ?? , | | 1b ?
?
,则 | 2 | (a b? ?
?? )
A. 3 B. 19 C.19 D. 2 3
5.已知3a e? , 3 3log 5 log 2b ? ? , 2 3c ln? ,则 a、 b、 c的大小关系为 ( )
A. a c b? ? B. b c a? ? C. c a b? ? D. c b a? ?
6.函数 ( ) 3f x x lgx? ? ? 零点所在区间为 ( )
A. (0,1) B. (1,2) C. (2,3) D. (3,4)
7.甲、乙两班在我校举行的“勿忘国耻,振兴中华”合唱比赛中,7位评委的评分情况如
茎叶图所示,其中甲班成绩的中位数是 81,乙班成绩的平均数是 86,若正实数 a、b满足:
a,G, b成等差数列且 x,G, y成等比数列,则 1 4
a b
? 的最小值为 ( )
A. 4
9
B.2 C.8 D. 9
4
- 2 -
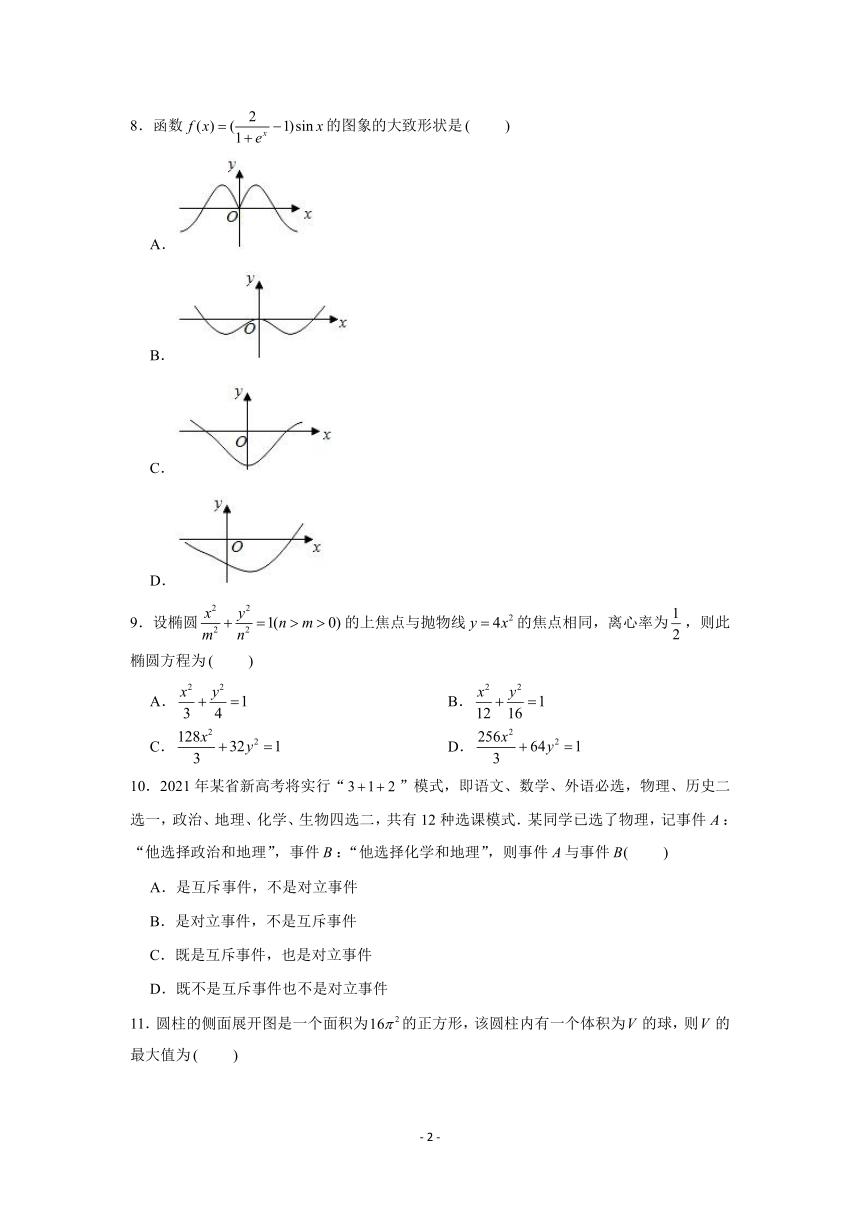
8.函数 2( ) ( 1)sin
1 x
f x x
e
? ?
?
的图象的大致形状是 ( )
A.
B.
C.
D.
9.设椭圆
2 2
2 2 1( 0)
x y n m
m n
? ? ? ? 的上焦点与抛物线 24y x? 的焦点相同,离心率为 1
2
,则此
椭圆方程为 ( )
A.
2 2
1
3 4
x y
? ? B.
2 2
1
12 16
x y
? ?
C.
2
2128 32 1
3
x y? ? D.
2
2256 64 1
3
x y? ?
10.2021年某省新高考将实行“3 1 2? ? ”模式,即语文、数学、外语必选,物理、历史二
选一,政治、地理、化学、生物四选二,共有 12种选课模式.某同学已选了物理,记事件 A:
“他选择政治和地理”,事件 B:“他选择化学和地理”,则事件 A与事件 (B )
A.是互斥事件,不是对立事件
B.是对立事件,不是互斥事件
C.既是互斥事件,也是对立事件
D.既不是互斥事件也不是对立事件
11.圆柱的侧面展开图是一个面积为 216? 的正方形,该圆柱内有一个体积为V 的球,则V 的
最大值为 ( )
- 3 -
A. 32
3
? B.
432
3
? C. 256
3
? D.
4256
3
?
12.已知锐角 ABC? 的角 A, B,C 的对边分别为 a, b, c,且 1c ? ,三角形 ABC的面
积 1ABCS? ? ,则
2 2a b? 的取值范围为 ( )
A. 17[ , )
2
?? B. (9, )?? C. 17[
2
, 9] D. 17[
2
, 9)
二、填空题:本大题共 4 小题,每小题 5 分,满分 20 分.
13.不等式 1 2x
x
?
? 的解集为 .
14.已知数列{ }na 中, 1 1a ? , 1 1n na a n? ? ? ? ,则数列{ }na 的通项公式是 .
15.已知一组数 1,2,m,6,7的平均数为 4,则这组数的方差为
16.已知函数 1
| 1 |,0 2
( ) 1( ) ,2 3
2
x
x x
f x
x?
??
?? ?
???
? ?
?
,若存在实数 1x , 2x , 3x ,当 1 2 30 3x x x? ?? ? 时,
1 2 3( ) ( ) ( )f x f x f x? ? ,则 1 2 2 3( ) ( )x x x f x? 的取值范围是 .
三、解答题:共 70 分.解答应写出文字说明、证明过程或演算步骤.
17.已知函数 ( ) 2cos ( 3 sin cos )f x x x x? ? .
(Ⅰ)求函数 ( )f x 的最小正周期和对称中心坐标;
(Ⅱ)讨论 ( )f x 在区间 [0, ]
2
?
上的单调性.
18.已知{ }na 是公差不为零的等差数列, 1 1a ? ,且 1a , 2a , 5a 成等比数列.
(1)求数列{ }na 的通项公式;
(2)设数列
1
12 nan
n n
b
a a ?
? ? ,求数列{ }nb 的前 n项和 nS .
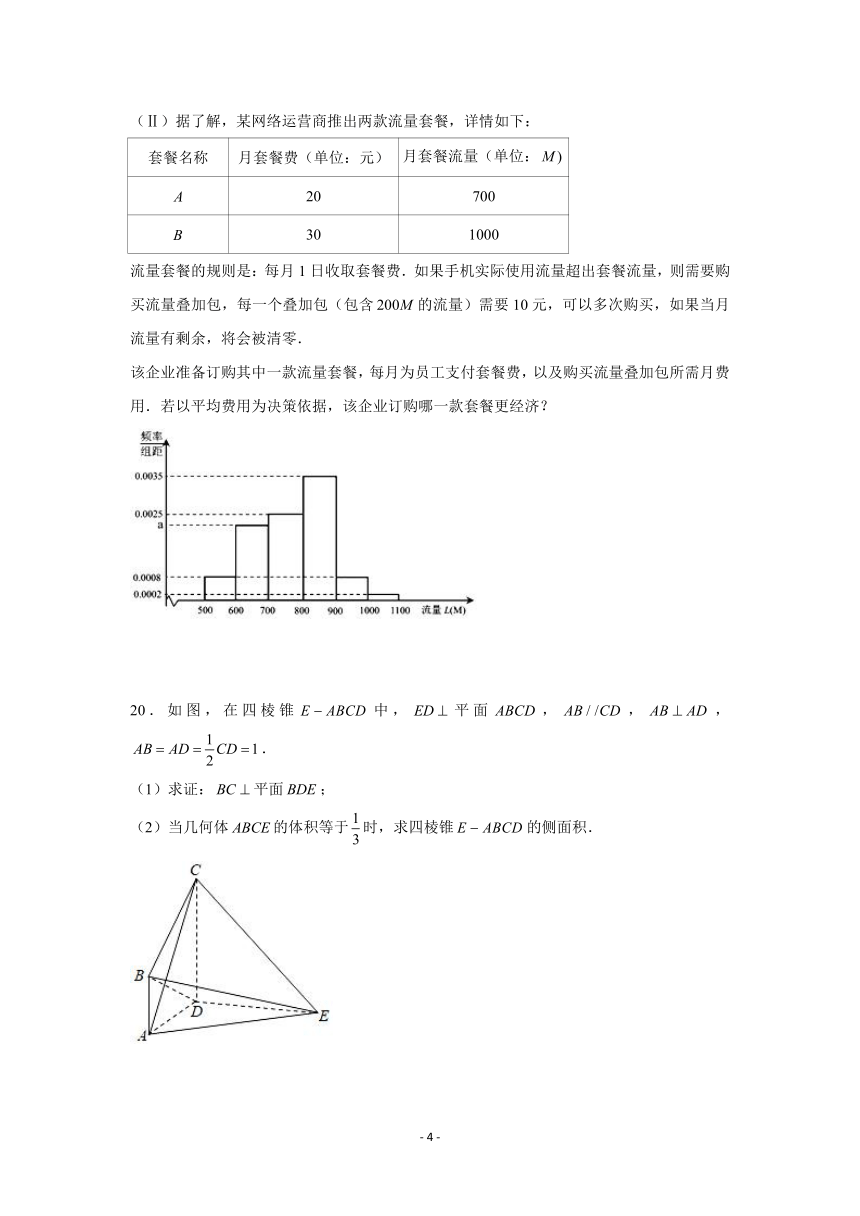
19.某大型企业为鼓励员工利用网络进行营销,准备为员工办理手机流量套餐.为了解员工
手机流量使用情况,通过抽样,得到 100位员工每人手机月平均使用流量 L(单位: )M 的
数据,其频率分布直方图如图.
(Ⅰ)从该企业的 100位员工中随机抽取 1人,求手机月平均使用流量不超过 900M 的概率;
- 4 -
(Ⅱ)据了解,某网络运营商推出两款流量套餐,详情如下:
套餐名称 月套餐费(单位:元) 月套餐流量(单位: )M
A 20 700
B 30 1000
流量套餐的规则是:每月 1日收取套餐费.如果手机实际使用流量超出套餐流量,则需要购
买流量叠加包,每一个叠加包(包含 200M 的流量)需要 10元,可以多次购买,如果当月
流量有剩余,将会被清零.
该企业准备订购其中一款流量套餐,每月为员工支付套餐费,以及购买流量叠加包所需月费
用.若以平均费用为决策依据,该企业订购哪一款套餐更经济?
20.如图,在四棱锥 E ABCD? 中, ED ? 平面 ABCD , / /AB CD , AB AD? ,
1 1
2
AB AD CD? ? ? .
(1)求证: BC ?平面 BDE;
(2)当几何体 ABCE的体积等于 1
3
时,求四棱锥 E ABCD? 的侧面积.
- 5 -
21.已知 ( 2,0)A ? , (1,0)B , (6,0)Q ,若动点 ( , )P x y? ? 满足 | | 2 | |PA PB? ,设线段 PQ的中点
为M
(1)求点M 的轨迹方程;
(2)设直线 1y kx? ? 与点 M 的轨迹交于不同的两点 1(C x , 1)y , 2(D x , 2 )y ,且满足
1 2 2
1| |
1
x x
k
? ?
?
,求直线 l的方程.
22.已知函数 | |( ) x af x e ?? , ( ) bxh x e?
(1)若 2a ? , 1b ? ,判断 ( ) ( ) ( )g x f x h x? ? 在 ( ,1)?? 上的单调性,并用定义证明;
(2)已知 [0b? , 2)ln ,存在 0 [0x ? ,1],对任意 [0x? ,1],都有 0| ( ) ( ) | 1f x h x? ? 成立,
求 a的取值范围.
- 6 -
2019-2020 学年陕西省汉中市高二(上)期中数学试卷(文科)
参考答案与试题解析
一、选择题:本大题共 12 小题,每小题 5 分,满分 60 分,在每小题给出的四个选项中,
只有一项是符合题目要求的.
1.已知集合 { 1A ? ? ,0,1}, { | 2 1}xB x? ? ,则 (A B ?? )
A.{ 1? ,0,1} B.{ 1? , 0} C.{0,1} D.{ 1? ,1}
【解答】解: { 1A ? ?? ,0,1}, { | 0}B x x? ? ,
{ 1A B? ? ?? , 0}.
故选: B.
2.命题“存在 x R? , 2 1 0x x? ? ? 的否定是 ( )
A.不存在 x R? , 2 1 0x x? ? ? B.存在 x R? , 2 2 0x x? ? ?
C.对任意的 x R? , 2 1 0x x? ? ? D.对任意的 x R? , 2 1 0x x? ? ?
【解答】解:因为特称命题的否定是全称命题,所以,命题“存在 x R? , 2 1 0x x? ? ? 的否
定是:对任意的 x R? , 2 1 0x x? ? ? .
故选: D.
3.小明出国旅游,当地时间比中国时间晚一个小时,他需要将表的时针旋转,则转过的角
的弧度数是 ( )
A.
3
? B.
6
? C.
3
?
? D.
6
?
?
【解答】解:他需要将表的时针逆时针旋转,则转过的角的弧度数是
6
?
,
故选: B.
4.平面向量 a?与 b
?
的夹角为 60?,且 (3,0)a ?? , | | 1b ?
?
,则 | 2 | (a b? ?
?? )
A. 3 B. 19 C.19 D. 2 3
【解答】解:平面向量 a?与 b
?
的夹角为 60?, (3,0)a ?? , | | 1b ?
?
,
| | 3a? ?? ,
? 2 2 2( 2 ) 4 4 9 4 3 1 cos60 4 1 19a b a a b b? ? ? ? ? ? ? ? ? ? ? ? ?
? ? ?? ? ?? ,
- 7 -
| 2 | 19a b? ? ?
??
.
故选: B.
5.已知3a e? , 3 3log 5 log 2b ? ? , 2 3c ln? ,则 a、 b、 c的大小关系为 ( )
A. a c b? ? B. b c a? ? C. c a b? ? D. c b a? ?
【解答】解: 3 3
5, , 3
2
a log e b log c ln? ? ? ,
? 3 3 3
5 3 1, 3 1
2
log log e log ln lne? ? ? ? ? ,
c a b? ? ? .
故选:C.
6.函数 ( ) 3f x x lgx? ? ? 零点所在区间为 ( )
A. (0,1) B. (1,2) C. (2,3) D. (3,4)
【解答】解:?函数 ( ) 3f x x lgx? ? ? 在定义域内是连续函数;
f (2) 2 3 2 0lg? ? ? ? , f (3) 3 3 3 3 0lg lg? ? ? ? ? ;
f? (2) f (3) 0? ,
根据零点存在性定理,
( )f x 的零点在区间 (2,3)上,
故选:C.
7.甲、乙两班在我校举行的“勿忘国耻,振兴中华”合唱比赛中,7位评委的评分情况如
茎叶图所示,其中甲班成绩的中位数是 81,乙班成绩的平均数是 86,若正实数 a、b满足:
a,G, b成等差数列且 x,G, y成等比数列,则 1 4
a b
? 的最小值为 ( )
A. 4
9
B.2 C.8 D. 9
4
【解答】因为甲的中位数为 81,故 1x ? ;
因为乙的平均数是 86,可求得 4y ? ;
因为 x,G, y成等比数列,所以 2 4G xy? ? ,
- 8 -
因为 a,G, b成等差数列,则 2G a b? ? ,且 a、 b为正实数,所以 4a b? ?
1 4 1 1 4 1 4 5 1 4 5 1 4 5 1 9( )( ) (1 4) ( ) 2 2 4
4 4 4 4 4 4 4 4 4
b a b a b aa b
a b a b a b a b a b
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??
故选: D.
8.函数 2( ) ( 1)sin
1 x
f x x
e
? ?
?
的图象的大致形状是 ( )
A.
B.
C.
D.
【解答】解: ( )f x? 的函数的定义域为 R,
2 2 2 2 2 2( ) ( 1)sin( ) ( 1)sin (2 1)sin ( 1)sin ( )
1 1 1 11
x
x x x
x
ef x x x x x f x
e e e
e
? ?
? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
? ? ??
( )f x? 为偶函数,
( )f x? 关于 y轴对称,
当 0x ? 时, (0) 0f ? ,
当 1x ? 时, f (1) 2( 1)sin1 0
1 e
? ? ?
?
,
故选: B.
9.设椭圆
2 2
2 2 1( 0)
x y n m
m n
? ? ? ? 的上焦点与抛物线 24y x? 的焦点相同,离心率为 1
2
,则此
椭圆方程为 ( )
- 9 -
A.
2 2
1
3 4
x y
? ? B.
2 2
1
12 16
x y
? ?
C.
2
2128 32 1
3
x y? ? D.
2
2256 64 1
3
x y? ?
【解答】解:?抛物线 24y x? 的焦点为 1(0, )
16
,椭圆焦点在 y轴上,
2 2
1
3 4
x y
? ? 的焦点坐
标 (0,1)排除 A;
2 2
1
12 16
x y
? ? 的焦点坐标 (0,2)排除 B,
由
1
2
e ? 排除C ,
故选: D.
10.2021年某省新高考将实行“3 1 2? ? ”模式,即语文、数学、外语必选,物理、历史二
选一,政治、地理、化学、生物四选二,共有 12种选课模式.某同学已选了物理,记事件 A:
“他选择政治和地理”,事件 B:“他选择化学和地理”,则事件 A与事件 (B )
A.是互斥事件,不是对立事件
B.是对立事件,不是互斥事件
C.既是互斥事件,也是对立事件
D.既不是互斥事件也不是对立事件
【解答】解:2021年某省新高考将实行“ 3 1 2? ? ”模式,
即语文、数学、外语必选,物理、历史二选一,政治、地理、化学、生物四选二,
共有 12种选课模式.某同学已选了物理,
记事件 A:“他选择政治和地理”,事件 B:“他选择化学和地理”,
则事件 A与事件 B不能同时发生,但能同时不发生,
故事件 A和 B是互斥事件,但不是对立事件,故 A正确.
故选: A.
11.圆柱的侧面展开图是一个面积为 216? 的正方形,该圆柱内有一个体积为V 的球,则V 的
最大值为 ( )
A. 32
3
? B.
432
3
? C. 256
3
? D.
4256
3
?
【解答】解:圆柱的侧面展开图是一个面积为 216? 的正方形,所以该圆柱的底面半径为
2 4r? ?? 解得 2r ? ,
圆柱的高为 4? ,该圆柱内有一个体积为V 的球,当球的最大圆的与圆柱的侧面相切时,该
- 10 -
球的体积最大值
34 2 32
3 3
V ? ?? ?? .
故选: A.
12.已知锐角 ABC? 的角 A, B,C 的对边分别为 a, b, c,且 1c ? ,三角形 ABC的面
积 1ABCS? ? ,则
2 2a b? 的取值范围为 ( )
A. 17[ , )
2
?? B. (9, )?? C. 17[
2
, 9] D. 17[
2
, 9)
【解答】解:因为三角形为锐角三角形,所以过C作CD AB? 于D,D在边 AB上,如图:
因为:
1 1
2ABC
S AB CD? ? ?? ,所以 2CD ? ,
在三角形 ADC中, 2 2 2 4AD AC CD b? ? ? ? ,
在三角形 BDC 中, 2 2 2 4BD BC CD a? ? ? ? ,
1AD BD AB? ? ?? ,? 2 24 4 1a b? ? ? ? ,
2 2 2 2 2 2 2 2 2 2 2 24 4 8 ( 4) ( 4) 8 ( 4) (1 4) 8a b a b a b a a? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
2 2 22( 4) 2 4 9a a? ? ? ? ?
? 2 4 (0,1)a ? ? .
2 2 17[
2
a b? ? ? , 9).
故选: D.
二、填空题:本大题共 4 小题,每小题 5 分,满分 20 分.
13.不等式 1 2x
x
?
? 的解集为 ( 1,0)? .
【解答】解:由
1 2x
x
?
? 可得
1 2 0x
x
?
? ? ,
整理可得,
1 0x
x
?
? ,
- 11 -
解可得,{ | 1 0}x x? ? ? .
故答案为: ( 1,0)?
14.已知数列{ }na 中, 1 1a ? , 1 1n na a n? ? ? ? ,则数列{ }na 的通项公式是
( 1)
2n
n na ?? .
【解答】解:数列{ }na 中, 1 1a ? , 1 1n na a n? ? ? ? ,
所以 1 1n na a n? ? ? ? ,
当 2n? 时, 1n na a n?? ? ,
进一步整理得, 1 2 1n na a n? ?? ? ? ,
?,
2 1 2a a? ? ,
所以 1 2 3na a n? ? ? ??? ,
则:
( 1)1 2 3
2n
n na n ?? ? ? ??? ? (首项符合通项).
故
( 1)
2n
n na ?? .
故答案为:
( 1)
2n
n na ??
15.已知一组数 1,2,m,6,7的平均数为 4,则这组数的方差为 26
5
【解答】解:数据 1,2,m,6,7的平均数为 4,
则
1 (1 2 6 7) 4
5
x m? ? ? ? ? ? ? ,
解得 4m ? ,
所以这组数的方差为
2 2 2 2 2 21 26[(1 4) (2 4) (4 4) (6 4) (7 4) ]
5 5
s ? ? ? ? ? ? ? ? ? ? ? ? .
故答案为:
26
5
.
16.已知函数 1
| 1 |,0 2
( ) 1( ) ,2 3
2
x
x x
f x
x?
??
?? ?
???
? ?
?
,若存在实数 1x , 2x , 3x ,当 1 2 30 3x x x? ?? ? 时,
1 2 3( ) ( ) ( )f x f x f x? ? ,则 1 2 2 3( ) ( )x x x f x? 的取值范围是
5[
8
,
3)
2
.
【解答】 解:分别画出 | 1 |y x? ? 与 11( )
2
xy ?? 的图象,如图所示
- 12 -
所以 1 2 2x x? ? , 3
1
1 2
11 1 ( )
2
xx x ?? ? ? ? ,得 3 12
1( ) 1
2
xx ?? ? ,得
则 3 31 11 2 2 3
1 1( ) ( ) 2(( ) 1) ( )
2 2
x xx x x f x ? ?? ? ? ? ,
令 3 1
1( )
2
xt ??? , 3 (2x ? , 3],得
1[
4
t? , 1)
2
,
又 22( 1) 2 2y t t t t? ? ? ? ,则 y的取值范围为 5[
8
,
3)
2
.
故答案为:
5[
8
,
3)
2
.
三、解答题:共 70 分.解答应写出文字说明、证明过程或演算步骤.
17.已知函数 ( ) 2cos ( 3 sin cos )f x x x x? ? .
(Ⅰ)求函数 ( )f x 的最小正周期和对称中心坐标;
(Ⅱ)讨论 ( )f x 在区间 [0, ]
2
?
上的单调性.
【解答】解:(Ⅰ) 2( ) 2cos ( 3 sin cos ) 3 sin 2 2f x x x x x cos x? ? ? ?
3 sin 2 cos2 1 2sin(2 ) 1
6
x x x ?? ? ? ? ? ? .
2
2
T ? ?? ? ? ,
由 2
6
x k? ?? ? ,得
12 2
kx ? ?? ? ? , k Z? .
( )f x? 的对称中心为 (
12 2
k? ?
? ? ,1), k Z? ;
(Ⅱ)由 2 2 2
2 6 2
k x k? ? ?? ?? ? ? ?? ? , k Z? .
解得
3 6
k x k? ?? ?? ? ?? ? , k Z? .
由
32 2 2
2 6 2
k x k? ? ?? ?? ? ?? ? , k Z? .
解得
2
6 3
k x k? ?? ?? ?? ? , k Z? .
- 13 -
取 0k ? ,可得 ( )f x 在区间 [0, ]
2
?
上的增区间为 [0, ]
6
?
,减区间为 (
6
?
, ]
2
?
.
18.已知{ }na 是公差不为零的等差数列, 1 1a ? ,且 1a , 2a , 5a 成等比数列.
(1)求数列{ }na 的通项公式;
(2)设数列
1
12 nan
n n
b
a a ?
? ? ,求数列{ }nb 的前 n项和 nS .
【解答】解:(1)已知{ }na 是公差 d不为零的等差数列, 1 1a ? ,且 1a , 2a , 5a 成等比数列.
所以 22 1 5a a a? ? ,整理得
2
1 1 1( ) ( 4 )a d a a d? ? ?? ,解得 2d ? .
故 1 2( 1) 2 1na a n n? ? ? ? ? .
(2)由于 2 1na n? ? ,
所以 2 1
1
1 1 4 1 1 12 2 ( )
(2 1)(2 1) 2 2 2 1 2 1
n
n
a n
n
n n
b
a a n n n n
?
?
? ? ? ? ? ? ?
? ? ? ?
,
所以 1 2
1 1 1 1 1 1 1(4 4 4 ) (1 )
2 2 3 3 5 2 1 2 1
n
nS n n
? ? ??? ? ? ? ? ??? ?
? ?
1 4(4 1) 1 1(1 )
2 4 1 2 2 1
n
n
?
? ? ?
? ?
? ,
2 (4 1)
3 2 1
n n
n
? ? ?
?
.
19.某大型企业为鼓励员工利用网络进行营销,准备为员工办理手机流量套餐.为了解员工
手机流量使用情况,通过抽样,得到 100位员工每人手机月平均使用流量 L(单位: )M 的
数据,其频率分布直方图如图.
(Ⅰ)从该企业的 100位员工中随机抽取 1人,求手机月平均使用流量不超过 900M 的概率;
(Ⅱ)据了解,某网络运营商推出两款流量套餐,详情如下:
套餐名称 月套餐费(单位:元) 月套餐流量(单位: )M
A 20 700
B 30 1000
流量套餐的规则是:每月 1日收取套餐费.如果手机实际使用流量超出套餐流量,则需要购
买流量叠加包,每一个叠加包(包含 200M 的流量)需要 10元,可以多次购买,如果当月
流量有剩余,将会被清零.
该企业准备订购其中一款流量套餐,每月为员工支付套餐费,以及购买流量叠加包所需月费
- 14 -
用.若以平均费用为决策依据,该企业订购哪一款套餐更经济?
【解答】解:(1)由题意知:
(0.0002 0.0008 0.0025 0.0035 0.0008) 100 1 0.00 22a a? ? ? ? ? ? ? ? ? .
所 以 100 位 员 工 每 人 手 机 月 平 均 使 用 流 量 不 超 过 900M 的 概 率 为
1 (0.0002 0.0008) 100 0.9? ? ? ? ,
(2)若该企业选择 A套餐,则 100位员工每人所需费用可能为 20元,30元,40元,
每月使用流量的平均费用为 20 (0.08 0.22) 30 (0.25 0.35) 40 (0.08 0.02) 28? ? ? ? ? ? ? ? ? ,
若该企业选择 B套餐,则 100位员工每人所需费用可能为 30元,40元,每月使用流量的平
均费用为 30 (0.08 0.22 0.25 0.35) 40 0.02 30.2? ? ? ? ? ? ? ,
所以该企业选择 A套餐更经济.
20.如图,在四棱锥 E ABCD? 中, ED ? 平面 ABCD , / /AB CD , AB AD? ,
1 1
2
AB AD CD? ? ? .
(1)求证: BC ?平面 BDE;
(2)当几何体 ABCE的体积等于 1
3
时,求四棱锥 E ABCD? 的侧面积.
【解答】解:(1)证明:取CD的中点 F ,连接 BF ,
则直角梯形 ABCD中, BF CD? , BF CF DF? ? ,
90CBD?? ? ?,即 BC BD? ,
- 15 -
又 ED ?平面 ABCD, BC ?平面 ABCD,
BC DE? ? ,
又 BD DE D?? ,
BC? ?平面 BDE;
(2) ED ?? 平面 ABCD,
DE AB? ? ,
又 AB AD? ,
AB? ? 平面 ADE ,
AB AE? ? ,
1 1 1 1
3 2 6 3A BCE E ABC
V V DE AB AD DE? ?? ? ? ? ? ? ? ?三棱锥 三棱锥 ,解得 2DE ? ,
又
1 1
2
AD CD? ? ,DE AD? ,
5EA? ? ,
又 1AB ? , 6BE? ? ;
又 BC ?平面 BDE, BC BE? ? , CBE? 是直角三角形;
?四棱锥 E ABCD? 的侧面积为
6 2 3 51 1 1 1
2 2 2 2 2
S DE AD AE AB DE CD BC BE
? ?
? ? ? ? ? ? ? ? ?侧 .
21.已知 ( 2,0)A ? , (1,0)B , (6,0)Q ,若动点 ( , )P x y? ? 满足 | | 2 | |PA PB? ,设线段 PQ的中点
为M
(1)求点M 的轨迹方程;
(2)设直线 1y kx? ? 与点 M 的轨迹交于不同的两点 1(C x , 1)y , 2(D x , 2 )y ,且满足
1 2 2
1| |
1
x x
k
? ?
?
,求直线 l的方程.
- 16 -
【解答】解:(1)因为 ( 2,0)A ? , (1,0)B , ( , )P x y? ? ,且 | | 2 | |PA PB?
所以 2 2 2 2( 2) 2 ( 1)x y x y? ? ? ?? ? ? ? ? ,
化简得 2 2 4 0x y x? ? ?? ? ? ,即 2 2( 2) 4x y? ?? ? ? ①
设 ( , )M x y ,由中点坐标公式得
6
2
2
xx
yy
? ?? ???
? ?? ?
??
,即
2 6
2
x x
y y
? ? ??
? ? ??
②
将②代入①得: 2 2(2 8) (2 ) 4x y? ? ?
所以点M 的轨迹方程为 2 2( 4) 1x y? ? ? ?
(2)由 2 2
1
( 4) 1
y kx
x y
? ??
? ? ? ??
消去 y得 2 2( 4) ( 1) 1x kx? ? ? ? ,
整理得 2 2(1 ) 2(4 ) 16 0k x k x? ? ? ? ? ,
所以 1 2 1 22 2
2(4 ) 16,
1 1
kx x x x
k k
?
? ? ?
? ?
? ,
由已知 1 2 2
1| |
1
x x
k
? ?
?
得 21 2 1 2 2 2
1( ) 4
(1 )
x x x x
k
? ? ?
?
? ,
所以
2
2 2 2 2 2
4(4 ) 16 14
(1 ) 1 (1 )
k
k k k
?
? ? ?
? ? ?
即 2 24(4 ) 64(1 ) 1k k? ? ? ? ,即 260 32 1 0k k? ? ?
所以 1 2
1 1,
2 30
k k? ?
所以直线 l的方程为 1 1
2
y x? ? 或 1 1
30
y x? ?
即 2 1 0x y? ? ? 或 30 30 0x y? ? ? ?
22.已知函数 | |( ) x af x e ?? , ( ) bxh x e?
(1)若 2a ? , 1b ? ,判断 ( ) ( ) ( )g x f x h x? ? 在 ( ,1)?? 上的单调性,并用定义证明;
(2)已知 [0b? , 2)ln ,存在 0 [0x ? ,1],对任意 [0x? ,1],都有 0| ( ) ( ) | 1f x h x? ? 成立,
求 a的取值范围.
【解答】解:(1) 2a ?? , 1b ? ,
| 2|( ) ( ) ( ) x xg x f x h x e e?? ? ? ? ? ,且 1x ? ,
2( ) x xg x e e?? ? ? , ( )y g x? 在 ( ,1)?? 上为减函数,
- 17 -
证明:任取 1x , 2 ( ,1)x ? ?? ,且 1 2x x? ,
2 1
1 2 2 1
1 2 1 2
2 2 2
1 2
( )( ) ( ) ( ) ( )
x x
x x x x
x x x x
e e e e eg x g x e e e e
e e e e
?
? ? ? ? ? ? ? ? ,
1 2
2 1
1 2
2
( )
x x
x x
x x
e e ee e
e e
?
? ? ,
1 2 1x x? ?? ,
? 2 1 0x xe e? ? , 1 2 1 22 x x x xe e e e?? ? ,
1 2( ) ( ) 0g x g x? ? ? ,即 1 2( ) ( )g x g x? ,
( )y g x? ? 在 ( ,1)?? 上为减函数.
(2) 0| ( ) ( ) | 1f x h x? ?? ,
0( ) 1 ( ) ( ) 1f x h x f x? ? ? ? ?
?对任意 [0x? ,1],存在 0 [0x ? ,1],
使得 0( ) 1 ( ) ( ) 1f x h x f x? ? ? ? 成立,
即存在 0 [0x ? ,1],使得 0( ( ) 1) ( ) ( ( ) 1)max minf x h x f x? ? ? ? ,
当 0 2b ln?? , ( )h x 为增函数或常函数,
01 ( ) 2
bh x e ?? ? ? ,
此时 0( ( ) 1) 1 2minf x e? ? ?? ,
则有 0( ) ( ( ) 1)minh x f x? ? 恒成立
当
1
2
a? 时, ( )maxf x f? (1) 1 ae ??
11b ae e ?? ? ?
1 ( 1)ba ln e? ? ? ?
? 1( 1) 2
2
bln e ln ln e? ? ??
11 ( 1)
2
bln e? ? ? ? ,
?
1(1 ( 1), ]
2
ba ln e? ? ?
当 a 1
2
? 时,
- 18 -
? ( ) (0) amaxf x f e? ?
1b ae e? ? ? ,
( 1)ba ln e? ? ?
1( 1) 2
2
bln e ln ln e? ? ?? ? ,
11 ( 1)
2
bln e? ? ? ? .
?
1( , ( 1))
2
ba ln e? ? ,
综上所述, (1 ( 1)ba ln e? ? ? , ( 1))bln e ? .
2019-2020 学年陕西省汉中市高二(上)期中数学试卷(文科)
一、选择题:本大题共 12 小题,每小题 5 分,满分 60 分,在每小题给出的四个选项中,
只有一项是符合题目要求的.
1.已知集合 { 1A ? ? ,0,1}, { | 2 1}xB x? ? ,则 (A B ?? )
A.{ 1? ,0,1} B.{ 1? , 0} C.{0,1} D.{ 1? ,1}
2.命题“存在 x R? , 2 1 0x x? ? ? 的否定是 ( )
A.不存在 x R? , 2 1 0x x? ? ? B.存在 x R? , 2 2 0x x? ? ?
C.对任意的 x R? , 2 1 0x x? ? ? D.对任意的 x R? , 2 1 0x x? ? ?
3.小明出国旅游,当地时间比中国时间晚一个小时,他需要将表的时针旋转,则转过的角
的弧度数是 ( )
A.
3
? B.
6
? C.
3
?
? D.
6
?
?
4.平面向量 a?与 b
?
的夹角为 60?,且 (3,0)a ?? , | | 1b ?
?
,则 | 2 | (a b? ?
?? )
A. 3 B. 19 C.19 D. 2 3
5.已知3a e? , 3 3log 5 log 2b ? ? , 2 3c ln? ,则 a、 b、 c的大小关系为 ( )
A. a c b? ? B. b c a? ? C. c a b? ? D. c b a? ?
6.函数 ( ) 3f x x lgx? ? ? 零点所在区间为 ( )
A. (0,1) B. (1,2) C. (2,3) D. (3,4)
7.甲、乙两班在我校举行的“勿忘国耻,振兴中华”合唱比赛中,7位评委的评分情况如
茎叶图所示,其中甲班成绩的中位数是 81,乙班成绩的平均数是 86,若正实数 a、b满足:
a,G, b成等差数列且 x,G, y成等比数列,则 1 4
a b
? 的最小值为 ( )
A. 4
9
B.2 C.8 D. 9
4
- 2 -
8.函数 2( ) ( 1)sin
1 x
f x x
e
? ?
?
的图象的大致形状是 ( )
A.
B.
C.
D.
9.设椭圆
2 2
2 2 1( 0)
x y n m
m n
? ? ? ? 的上焦点与抛物线 24y x? 的焦点相同,离心率为 1
2
,则此
椭圆方程为 ( )
A.
2 2
1
3 4
x y
? ? B.
2 2
1
12 16
x y
? ?
C.
2
2128 32 1
3
x y? ? D.
2
2256 64 1
3
x y? ?
10.2021年某省新高考将实行“3 1 2? ? ”模式,即语文、数学、外语必选,物理、历史二
选一,政治、地理、化学、生物四选二,共有 12种选课模式.某同学已选了物理,记事件 A:
“他选择政治和地理”,事件 B:“他选择化学和地理”,则事件 A与事件 (B )
A.是互斥事件,不是对立事件
B.是对立事件,不是互斥事件
C.既是互斥事件,也是对立事件
D.既不是互斥事件也不是对立事件
11.圆柱的侧面展开图是一个面积为 216? 的正方形,该圆柱内有一个体积为V 的球,则V 的
最大值为 ( )
- 3 -
A. 32
3
? B.
432
3
? C. 256
3
? D.
4256
3
?
12.已知锐角 ABC? 的角 A, B,C 的对边分别为 a, b, c,且 1c ? ,三角形 ABC的面
积 1ABCS? ? ,则
2 2a b? 的取值范围为 ( )
A. 17[ , )
2
?? B. (9, )?? C. 17[
2
, 9] D. 17[
2
, 9)
二、填空题:本大题共 4 小题,每小题 5 分,满分 20 分.
13.不等式 1 2x
x
?
? 的解集为 .
14.已知数列{ }na 中, 1 1a ? , 1 1n na a n? ? ? ? ,则数列{ }na 的通项公式是 .
15.已知一组数 1,2,m,6,7的平均数为 4,则这组数的方差为
16.已知函数 1
| 1 |,0 2
( ) 1( ) ,2 3
2
x
x x
f x
x?
??
?? ?
???
? ?
?
,若存在实数 1x , 2x , 3x ,当 1 2 30 3x x x? ?? ? 时,
1 2 3( ) ( ) ( )f x f x f x? ? ,则 1 2 2 3( ) ( )x x x f x? 的取值范围是 .
三、解答题:共 70 分.解答应写出文字说明、证明过程或演算步骤.
17.已知函数 ( ) 2cos ( 3 sin cos )f x x x x? ? .
(Ⅰ)求函数 ( )f x 的最小正周期和对称中心坐标;
(Ⅱ)讨论 ( )f x 在区间 [0, ]
2
?
上的单调性.
18.已知{ }na 是公差不为零的等差数列, 1 1a ? ,且 1a , 2a , 5a 成等比数列.
(1)求数列{ }na 的通项公式;
(2)设数列
1
12 nan
n n
b
a a ?
? ? ,求数列{ }nb 的前 n项和 nS .
19.某大型企业为鼓励员工利用网络进行营销,准备为员工办理手机流量套餐.为了解员工
手机流量使用情况,通过抽样,得到 100位员工每人手机月平均使用流量 L(单位: )M 的
数据,其频率分布直方图如图.
(Ⅰ)从该企业的 100位员工中随机抽取 1人,求手机月平均使用流量不超过 900M 的概率;
- 4 -
(Ⅱ)据了解,某网络运营商推出两款流量套餐,详情如下:
套餐名称 月套餐费(单位:元) 月套餐流量(单位: )M
A 20 700
B 30 1000
流量套餐的规则是:每月 1日收取套餐费.如果手机实际使用流量超出套餐流量,则需要购
买流量叠加包,每一个叠加包(包含 200M 的流量)需要 10元,可以多次购买,如果当月
流量有剩余,将会被清零.
该企业准备订购其中一款流量套餐,每月为员工支付套餐费,以及购买流量叠加包所需月费
用.若以平均费用为决策依据,该企业订购哪一款套餐更经济?
20.如图,在四棱锥 E ABCD? 中, ED ? 平面 ABCD , / /AB CD , AB AD? ,
1 1
2
AB AD CD? ? ? .
(1)求证: BC ?平面 BDE;
(2)当几何体 ABCE的体积等于 1
3
时,求四棱锥 E ABCD? 的侧面积.
- 5 -
21.已知 ( 2,0)A ? , (1,0)B , (6,0)Q ,若动点 ( , )P x y? ? 满足 | | 2 | |PA PB? ,设线段 PQ的中点
为M
(1)求点M 的轨迹方程;
(2)设直线 1y kx? ? 与点 M 的轨迹交于不同的两点 1(C x , 1)y , 2(D x , 2 )y ,且满足
1 2 2
1| |
1
x x
k
? ?
?
,求直线 l的方程.
22.已知函数 | |( ) x af x e ?? , ( ) bxh x e?
(1)若 2a ? , 1b ? ,判断 ( ) ( ) ( )g x f x h x? ? 在 ( ,1)?? 上的单调性,并用定义证明;
(2)已知 [0b? , 2)ln ,存在 0 [0x ? ,1],对任意 [0x? ,1],都有 0| ( ) ( ) | 1f x h x? ? 成立,
求 a的取值范围.
- 6 -
2019-2020 学年陕西省汉中市高二(上)期中数学试卷(文科)
参考答案与试题解析
一、选择题:本大题共 12 小题,每小题 5 分,满分 60 分,在每小题给出的四个选项中,
只有一项是符合题目要求的.
1.已知集合 { 1A ? ? ,0,1}, { | 2 1}xB x? ? ,则 (A B ?? )
A.{ 1? ,0,1} B.{ 1? , 0} C.{0,1} D.{ 1? ,1}
【解答】解: { 1A ? ?? ,0,1}, { | 0}B x x? ? ,
{ 1A B? ? ?? , 0}.
故选: B.
2.命题“存在 x R? , 2 1 0x x? ? ? 的否定是 ( )
A.不存在 x R? , 2 1 0x x? ? ? B.存在 x R? , 2 2 0x x? ? ?
C.对任意的 x R? , 2 1 0x x? ? ? D.对任意的 x R? , 2 1 0x x? ? ?
【解答】解:因为特称命题的否定是全称命题,所以,命题“存在 x R? , 2 1 0x x? ? ? 的否
定是:对任意的 x R? , 2 1 0x x? ? ? .
故选: D.
3.小明出国旅游,当地时间比中国时间晚一个小时,他需要将表的时针旋转,则转过的角
的弧度数是 ( )
A.
3
? B.
6
? C.
3
?
? D.
6
?
?
【解答】解:他需要将表的时针逆时针旋转,则转过的角的弧度数是
6
?
,
故选: B.
4.平面向量 a?与 b
?
的夹角为 60?,且 (3,0)a ?? , | | 1b ?
?
,则 | 2 | (a b? ?
?? )
A. 3 B. 19 C.19 D. 2 3
【解答】解:平面向量 a?与 b
?
的夹角为 60?, (3,0)a ?? , | | 1b ?
?
,
| | 3a? ?? ,
? 2 2 2( 2 ) 4 4 9 4 3 1 cos60 4 1 19a b a a b b? ? ? ? ? ? ? ? ? ? ? ? ?
? ? ?? ? ?? ,
- 7 -
| 2 | 19a b? ? ?
??
.
故选: B.
5.已知3a e? , 3 3log 5 log 2b ? ? , 2 3c ln? ,则 a、 b、 c的大小关系为 ( )
A. a c b? ? B. b c a? ? C. c a b? ? D. c b a? ?
【解答】解: 3 3
5, , 3
2
a log e b log c ln? ? ? ,
? 3 3 3
5 3 1, 3 1
2
log log e log ln lne? ? ? ? ? ,
c a b? ? ? .
故选:C.
6.函数 ( ) 3f x x lgx? ? ? 零点所在区间为 ( )
A. (0,1) B. (1,2) C. (2,3) D. (3,4)
【解答】解:?函数 ( ) 3f x x lgx? ? ? 在定义域内是连续函数;
f (2) 2 3 2 0lg? ? ? ? , f (3) 3 3 3 3 0lg lg? ? ? ? ? ;
f? (2) f (3) 0? ,
根据零点存在性定理,
( )f x 的零点在区间 (2,3)上,
故选:C.
7.甲、乙两班在我校举行的“勿忘国耻,振兴中华”合唱比赛中,7位评委的评分情况如
茎叶图所示,其中甲班成绩的中位数是 81,乙班成绩的平均数是 86,若正实数 a、b满足:
a,G, b成等差数列且 x,G, y成等比数列,则 1 4
a b
? 的最小值为 ( )
A. 4
9
B.2 C.8 D. 9
4
【解答】因为甲的中位数为 81,故 1x ? ;
因为乙的平均数是 86,可求得 4y ? ;
因为 x,G, y成等比数列,所以 2 4G xy? ? ,
- 8 -
因为 a,G, b成等差数列,则 2G a b? ? ,且 a、 b为正实数,所以 4a b? ?
1 4 1 1 4 1 4 5 1 4 5 1 4 5 1 9( )( ) (1 4) ( ) 2 2 4
4 4 4 4 4 4 4 4 4
b a b a b aa b
a b a b a b a b a b
? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ??
故选: D.
8.函数 2( ) ( 1)sin
1 x
f x x
e
? ?
?
的图象的大致形状是 ( )
A.
B.
C.
D.
【解答】解: ( )f x? 的函数的定义域为 R,
2 2 2 2 2 2( ) ( 1)sin( ) ( 1)sin (2 1)sin ( 1)sin ( )
1 1 1 11
x
x x x
x
ef x x x x x f x
e e e
e
? ?
? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
? ? ??
( )f x? 为偶函数,
( )f x? 关于 y轴对称,
当 0x ? 时, (0) 0f ? ,
当 1x ? 时, f (1) 2( 1)sin1 0
1 e
? ? ?
?
,
故选: B.
9.设椭圆
2 2
2 2 1( 0)
x y n m
m n
? ? ? ? 的上焦点与抛物线 24y x? 的焦点相同,离心率为 1
2
,则此
椭圆方程为 ( )
- 9 -
A.
2 2
1
3 4
x y
? ? B.
2 2
1
12 16
x y
? ?
C.
2
2128 32 1
3
x y? ? D.
2
2256 64 1
3
x y? ?
【解答】解:?抛物线 24y x? 的焦点为 1(0, )
16
,椭圆焦点在 y轴上,
2 2
1
3 4
x y
? ? 的焦点坐
标 (0,1)排除 A;
2 2
1
12 16
x y
? ? 的焦点坐标 (0,2)排除 B,
由
1
2
e ? 排除C ,
故选: D.
10.2021年某省新高考将实行“3 1 2? ? ”模式,即语文、数学、外语必选,物理、历史二
选一,政治、地理、化学、生物四选二,共有 12种选课模式.某同学已选了物理,记事件 A:
“他选择政治和地理”,事件 B:“他选择化学和地理”,则事件 A与事件 (B )
A.是互斥事件,不是对立事件
B.是对立事件,不是互斥事件
C.既是互斥事件,也是对立事件
D.既不是互斥事件也不是对立事件
【解答】解:2021年某省新高考将实行“ 3 1 2? ? ”模式,
即语文、数学、外语必选,物理、历史二选一,政治、地理、化学、生物四选二,
共有 12种选课模式.某同学已选了物理,
记事件 A:“他选择政治和地理”,事件 B:“他选择化学和地理”,
则事件 A与事件 B不能同时发生,但能同时不发生,
故事件 A和 B是互斥事件,但不是对立事件,故 A正确.
故选: A.
11.圆柱的侧面展开图是一个面积为 216? 的正方形,该圆柱内有一个体积为V 的球,则V 的
最大值为 ( )
A. 32
3
? B.
432
3
? C. 256
3
? D.
4256
3
?
【解答】解:圆柱的侧面展开图是一个面积为 216? 的正方形,所以该圆柱的底面半径为
2 4r? ?? 解得 2r ? ,
圆柱的高为 4? ,该圆柱内有一个体积为V 的球,当球的最大圆的与圆柱的侧面相切时,该
- 10 -
球的体积最大值
34 2 32
3 3
V ? ?? ?? .
故选: A.
12.已知锐角 ABC? 的角 A, B,C 的对边分别为 a, b, c,且 1c ? ,三角形 ABC的面
积 1ABCS? ? ,则
2 2a b? 的取值范围为 ( )
A. 17[ , )
2
?? B. (9, )?? C. 17[
2
, 9] D. 17[
2
, 9)
【解答】解:因为三角形为锐角三角形,所以过C作CD AB? 于D,D在边 AB上,如图:
因为:
1 1
2ABC
S AB CD? ? ?? ,所以 2CD ? ,
在三角形 ADC中, 2 2 2 4AD AC CD b? ? ? ? ,
在三角形 BDC 中, 2 2 2 4BD BC CD a? ? ? ? ,
1AD BD AB? ? ?? ,? 2 24 4 1a b? ? ? ? ,
2 2 2 2 2 2 2 2 2 2 2 24 4 8 ( 4) ( 4) 8 ( 4) (1 4) 8a b a b a b a a? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ? ?
2 2 22( 4) 2 4 9a a? ? ? ? ?
? 2 4 (0,1)a ? ? .
2 2 17[
2
a b? ? ? , 9).
故选: D.
二、填空题:本大题共 4 小题,每小题 5 分,满分 20 分.
13.不等式 1 2x
x
?
? 的解集为 ( 1,0)? .
【解答】解:由
1 2x
x
?
? 可得
1 2 0x
x
?
? ? ,
整理可得,
1 0x
x
?
? ,
- 11 -
解可得,{ | 1 0}x x? ? ? .
故答案为: ( 1,0)?
14.已知数列{ }na 中, 1 1a ? , 1 1n na a n? ? ? ? ,则数列{ }na 的通项公式是
( 1)
2n
n na ?? .
【解答】解:数列{ }na 中, 1 1a ? , 1 1n na a n? ? ? ? ,
所以 1 1n na a n? ? ? ? ,
当 2n? 时, 1n na a n?? ? ,
进一步整理得, 1 2 1n na a n? ?? ? ? ,
?,
2 1 2a a? ? ,
所以 1 2 3na a n? ? ? ??? ,
则:
( 1)1 2 3
2n
n na n ?? ? ? ??? ? (首项符合通项).
故
( 1)
2n
n na ?? .
故答案为:
( 1)
2n
n na ??
15.已知一组数 1,2,m,6,7的平均数为 4,则这组数的方差为 26
5
【解答】解:数据 1,2,m,6,7的平均数为 4,
则
1 (1 2 6 7) 4
5
x m? ? ? ? ? ? ? ,
解得 4m ? ,
所以这组数的方差为
2 2 2 2 2 21 26[(1 4) (2 4) (4 4) (6 4) (7 4) ]
5 5
s ? ? ? ? ? ? ? ? ? ? ? ? .
故答案为:
26
5
.
16.已知函数 1
| 1 |,0 2
( ) 1( ) ,2 3
2
x
x x
f x
x?
??
?? ?
???
? ?
?
,若存在实数 1x , 2x , 3x ,当 1 2 30 3x x x? ?? ? 时,
1 2 3( ) ( ) ( )f x f x f x? ? ,则 1 2 2 3( ) ( )x x x f x? 的取值范围是
5[
8
,
3)
2
.
【解答】 解:分别画出 | 1 |y x? ? 与 11( )
2
xy ?? 的图象,如图所示
- 12 -
所以 1 2 2x x? ? , 3
1
1 2
11 1 ( )
2
xx x ?? ? ? ? ,得 3 12
1( ) 1
2
xx ?? ? ,得
则 3 31 11 2 2 3
1 1( ) ( ) 2(( ) 1) ( )
2 2
x xx x x f x ? ?? ? ? ? ,
令 3 1
1( )
2
xt ??? , 3 (2x ? , 3],得
1[
4
t? , 1)
2
,
又 22( 1) 2 2y t t t t? ? ? ? ,则 y的取值范围为 5[
8
,
3)
2
.
故答案为:
5[
8
,
3)
2
.
三、解答题:共 70 分.解答应写出文字说明、证明过程或演算步骤.
17.已知函数 ( ) 2cos ( 3 sin cos )f x x x x? ? .
(Ⅰ)求函数 ( )f x 的最小正周期和对称中心坐标;
(Ⅱ)讨论 ( )f x 在区间 [0, ]
2
?
上的单调性.
【解答】解:(Ⅰ) 2( ) 2cos ( 3 sin cos ) 3 sin 2 2f x x x x x cos x? ? ? ?
3 sin 2 cos2 1 2sin(2 ) 1
6
x x x ?? ? ? ? ? ? .
2
2
T ? ?? ? ? ,
由 2
6
x k? ?? ? ,得
12 2
kx ? ?? ? ? , k Z? .
( )f x? 的对称中心为 (
12 2
k? ?
? ? ,1), k Z? ;
(Ⅱ)由 2 2 2
2 6 2
k x k? ? ?? ?? ? ? ?? ? , k Z? .
解得
3 6
k x k? ?? ?? ? ?? ? , k Z? .
由
32 2 2
2 6 2
k x k? ? ?? ?? ? ?? ? , k Z? .
解得
2
6 3
k x k? ?? ?? ?? ? , k Z? .
- 13 -
取 0k ? ,可得 ( )f x 在区间 [0, ]
2
?
上的增区间为 [0, ]
6
?
,减区间为 (
6
?
, ]
2
?
.
18.已知{ }na 是公差不为零的等差数列, 1 1a ? ,且 1a , 2a , 5a 成等比数列.
(1)求数列{ }na 的通项公式;
(2)设数列
1
12 nan
n n
b
a a ?
? ? ,求数列{ }nb 的前 n项和 nS .
【解答】解:(1)已知{ }na 是公差 d不为零的等差数列, 1 1a ? ,且 1a , 2a , 5a 成等比数列.
所以 22 1 5a a a? ? ,整理得
2
1 1 1( ) ( 4 )a d a a d? ? ?? ,解得 2d ? .
故 1 2( 1) 2 1na a n n? ? ? ? ? .
(2)由于 2 1na n? ? ,
所以 2 1
1
1 1 4 1 1 12 2 ( )
(2 1)(2 1) 2 2 2 1 2 1
n
n
a n
n
n n
b
a a n n n n
?
?
? ? ? ? ? ? ?
? ? ? ?
,
所以 1 2
1 1 1 1 1 1 1(4 4 4 ) (1 )
2 2 3 3 5 2 1 2 1
n
nS n n
? ? ??? ? ? ? ? ??? ?
? ?
1 4(4 1) 1 1(1 )
2 4 1 2 2 1
n
n
?
? ? ?
? ?
? ,
2 (4 1)
3 2 1
n n
n
? ? ?
?
.
19.某大型企业为鼓励员工利用网络进行营销,准备为员工办理手机流量套餐.为了解员工
手机流量使用情况,通过抽样,得到 100位员工每人手机月平均使用流量 L(单位: )M 的
数据,其频率分布直方图如图.
(Ⅰ)从该企业的 100位员工中随机抽取 1人,求手机月平均使用流量不超过 900M 的概率;
(Ⅱ)据了解,某网络运营商推出两款流量套餐,详情如下:
套餐名称 月套餐费(单位:元) 月套餐流量(单位: )M
A 20 700
B 30 1000
流量套餐的规则是:每月 1日收取套餐费.如果手机实际使用流量超出套餐流量,则需要购
买流量叠加包,每一个叠加包(包含 200M 的流量)需要 10元,可以多次购买,如果当月
流量有剩余,将会被清零.
该企业准备订购其中一款流量套餐,每月为员工支付套餐费,以及购买流量叠加包所需月费
- 14 -
用.若以平均费用为决策依据,该企业订购哪一款套餐更经济?
【解答】解:(1)由题意知:
(0.0002 0.0008 0.0025 0.0035 0.0008) 100 1 0.00 22a a? ? ? ? ? ? ? ? ? .
所 以 100 位 员 工 每 人 手 机 月 平 均 使 用 流 量 不 超 过 900M 的 概 率 为
1 (0.0002 0.0008) 100 0.9? ? ? ? ,
(2)若该企业选择 A套餐,则 100位员工每人所需费用可能为 20元,30元,40元,
每月使用流量的平均费用为 20 (0.08 0.22) 30 (0.25 0.35) 40 (0.08 0.02) 28? ? ? ? ? ? ? ? ? ,
若该企业选择 B套餐,则 100位员工每人所需费用可能为 30元,40元,每月使用流量的平
均费用为 30 (0.08 0.22 0.25 0.35) 40 0.02 30.2? ? ? ? ? ? ? ,
所以该企业选择 A套餐更经济.
20.如图,在四棱锥 E ABCD? 中, ED ? 平面 ABCD , / /AB CD , AB AD? ,
1 1
2
AB AD CD? ? ? .
(1)求证: BC ?平面 BDE;
(2)当几何体 ABCE的体积等于 1
3
时,求四棱锥 E ABCD? 的侧面积.
【解答】解:(1)证明:取CD的中点 F ,连接 BF ,
则直角梯形 ABCD中, BF CD? , BF CF DF? ? ,
90CBD?? ? ?,即 BC BD? ,
- 15 -
又 ED ?平面 ABCD, BC ?平面 ABCD,
BC DE? ? ,
又 BD DE D?? ,
BC? ?平面 BDE;
(2) ED ?? 平面 ABCD,
DE AB? ? ,
又 AB AD? ,
AB? ? 平面 ADE ,
AB AE? ? ,
1 1 1 1
3 2 6 3A BCE E ABC
V V DE AB AD DE? ?? ? ? ? ? ? ? ?三棱锥 三棱锥 ,解得 2DE ? ,
又
1 1
2
AD CD? ? ,DE AD? ,
5EA? ? ,
又 1AB ? , 6BE? ? ;
又 BC ?平面 BDE, BC BE? ? , CBE? 是直角三角形;
?四棱锥 E ABCD? 的侧面积为
6 2 3 51 1 1 1
2 2 2 2 2
S DE AD AE AB DE CD BC BE
? ?
? ? ? ? ? ? ? ? ?侧 .
21.已知 ( 2,0)A ? , (1,0)B , (6,0)Q ,若动点 ( , )P x y? ? 满足 | | 2 | |PA PB? ,设线段 PQ的中点
为M
(1)求点M 的轨迹方程;
(2)设直线 1y kx? ? 与点 M 的轨迹交于不同的两点 1(C x , 1)y , 2(D x , 2 )y ,且满足
1 2 2
1| |
1
x x
k
? ?
?
,求直线 l的方程.
- 16 -
【解答】解:(1)因为 ( 2,0)A ? , (1,0)B , ( , )P x y? ? ,且 | | 2 | |PA PB?
所以 2 2 2 2( 2) 2 ( 1)x y x y? ? ? ?? ? ? ? ? ,
化简得 2 2 4 0x y x? ? ?? ? ? ,即 2 2( 2) 4x y? ?? ? ? ①
设 ( , )M x y ,由中点坐标公式得
6
2
2
xx
yy
? ?? ???
? ?? ?
??
,即
2 6
2
x x
y y
? ? ??
? ? ??
②
将②代入①得: 2 2(2 8) (2 ) 4x y? ? ?
所以点M 的轨迹方程为 2 2( 4) 1x y? ? ? ?
(2)由 2 2
1
( 4) 1
y kx
x y
? ??
? ? ? ??
消去 y得 2 2( 4) ( 1) 1x kx? ? ? ? ,
整理得 2 2(1 ) 2(4 ) 16 0k x k x? ? ? ? ? ,
所以 1 2 1 22 2
2(4 ) 16,
1 1
kx x x x
k k
?
? ? ?
? ?
? ,
由已知 1 2 2
1| |
1
x x
k
? ?
?
得 21 2 1 2 2 2
1( ) 4
(1 )
x x x x
k
? ? ?
?
? ,
所以
2
2 2 2 2 2
4(4 ) 16 14
(1 ) 1 (1 )
k
k k k
?
? ? ?
? ? ?
即 2 24(4 ) 64(1 ) 1k k? ? ? ? ,即 260 32 1 0k k? ? ?
所以 1 2
1 1,
2 30
k k? ?
所以直线 l的方程为 1 1
2
y x? ? 或 1 1
30
y x? ?
即 2 1 0x y? ? ? 或 30 30 0x y? ? ? ?
22.已知函数 | |( ) x af x e ?? , ( ) bxh x e?
(1)若 2a ? , 1b ? ,判断 ( ) ( ) ( )g x f x h x? ? 在 ( ,1)?? 上的单调性,并用定义证明;
(2)已知 [0b? , 2)ln ,存在 0 [0x ? ,1],对任意 [0x? ,1],都有 0| ( ) ( ) | 1f x h x? ? 成立,
求 a的取值范围.
【解答】解:(1) 2a ?? , 1b ? ,
| 2|( ) ( ) ( ) x xg x f x h x e e?? ? ? ? ? ,且 1x ? ,
2( ) x xg x e e?? ? ? , ( )y g x? 在 ( ,1)?? 上为减函数,
- 17 -
证明:任取 1x , 2 ( ,1)x ? ?? ,且 1 2x x? ,
2 1
1 2 2 1
1 2 1 2
2 2 2
1 2
( )( ) ( ) ( ) ( )
x x
x x x x
x x x x
e e e e eg x g x e e e e
e e e e
?
? ? ? ? ? ? ? ? ,
1 2
2 1
1 2
2
( )
x x
x x
x x
e e ee e
e e
?
? ? ,
1 2 1x x? ?? ,
? 2 1 0x xe e? ? , 1 2 1 22 x x x xe e e e?? ? ,
1 2( ) ( ) 0g x g x? ? ? ,即 1 2( ) ( )g x g x? ,
( )y g x? ? 在 ( ,1)?? 上为减函数.
(2) 0| ( ) ( ) | 1f x h x? ?? ,
0( ) 1 ( ) ( ) 1f x h x f x? ? ? ? ?
?对任意 [0x? ,1],存在 0 [0x ? ,1],
使得 0( ) 1 ( ) ( ) 1f x h x f x? ? ? ? 成立,
即存在 0 [0x ? ,1],使得 0( ( ) 1) ( ) ( ( ) 1)max minf x h x f x? ? ? ? ,
当 0 2b ln?? , ( )h x 为增函数或常函数,
01 ( ) 2
bh x e ?? ? ? ,
此时 0( ( ) 1) 1 2minf x e? ? ?? ,
则有 0( ) ( ( ) 1)minh x f x? ? 恒成立
当
1
2
a? 时, ( )maxf x f? (1) 1 ae ??
11b ae e ?? ? ?
1 ( 1)ba ln e? ? ? ?
? 1( 1) 2
2
bln e ln ln e? ? ??
11 ( 1)
2
bln e? ? ? ? ,
?
1(1 ( 1), ]
2
ba ln e? ? ?
当 a 1
2
? 时,
- 18 -
? ( ) (0) amaxf x f e? ?
1b ae e? ? ? ,
( 1)ba ln e? ? ?
1( 1) 2
2
bln e ln ln e? ? ?? ? ,
11 ( 1)
2
bln e? ? ? ? .
?
1( , ( 1))
2
ba ln e? ? ,
综上所述, (1 ( 1)ba ln e? ? ? , ( 1))bln e ? .
同课章节目录
