北师大版九年级数学下册第一章 直角三角形的边角关系5 三角函数的应用课件 (共20张)
文档属性
| 名称 | 北师大版九年级数学下册第一章 直角三角形的边角关系5 三角函数的应用课件 (共20张) |  | |
| 格式 | zip | ||
| 文件大小 | 3.9MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-30 19:29:46 | ||
图片预览




文档简介
(共20张PPT)
1.5三角函数的应用
1、直角三角形中各角之间的关系:
温故知新:
2、直角三角形中各边之间的关系:
3、直角三角形中边与角的关系:
4、解直角三角形需要哪些条件?
【自主梳理】
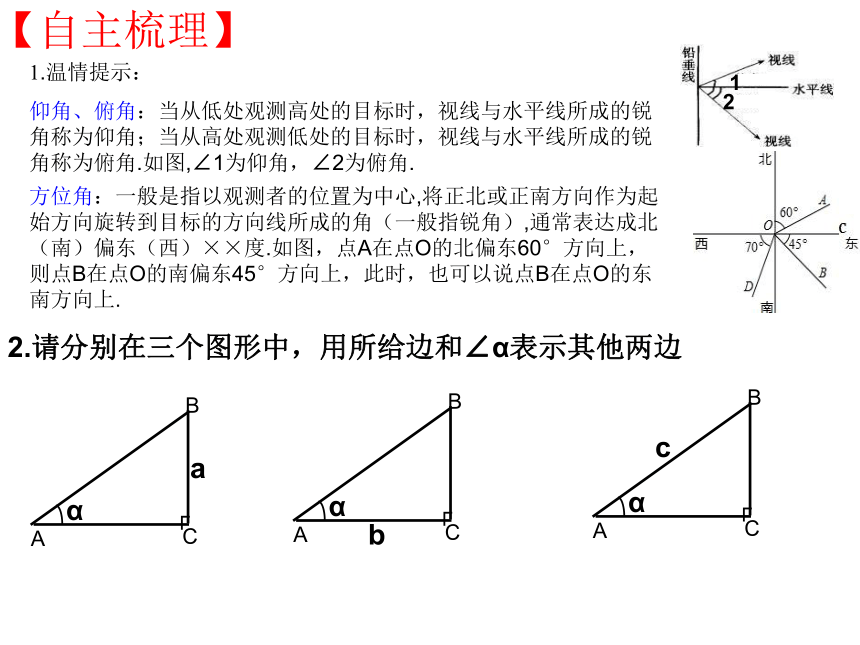
1.温情提示:
仰角、俯角:当从低处观测高处的目标时,视线与水平线所成的锐角称为仰角;当从高处观测低处的目标时,视线与水平线所成的锐角称为俯角.如图,∠1为仰角,∠2为俯角.
视线在水平线以上时,在视线所在的垂直平面内,视线与水平线所成的角叫做仰角. 俯角:在竖直面内的水平线与向下递降线段之间的角度(朝下看时,视线与水平面夹角为俯角)? 两者的范围都是0°到180°.
方位角:一般是指以观测者的位置为中心,将正北或正南方向作为起始方向旋转到目标的方向线所成的角(一般指锐角),通常表达成北(南)偏东(西)××度.如图,点A在点O的北偏东60°方向上,则点B在点O的南偏东45°方向上,此时,也可以说点B在点O的东南方向上.
2.请分别在三个图形中,用所给边和∠α表示其他两边
学习目标:
利用三角函数把实际问题转化为数学问题,进行有关三角函数的计算,并能对结果的意义进行说明。
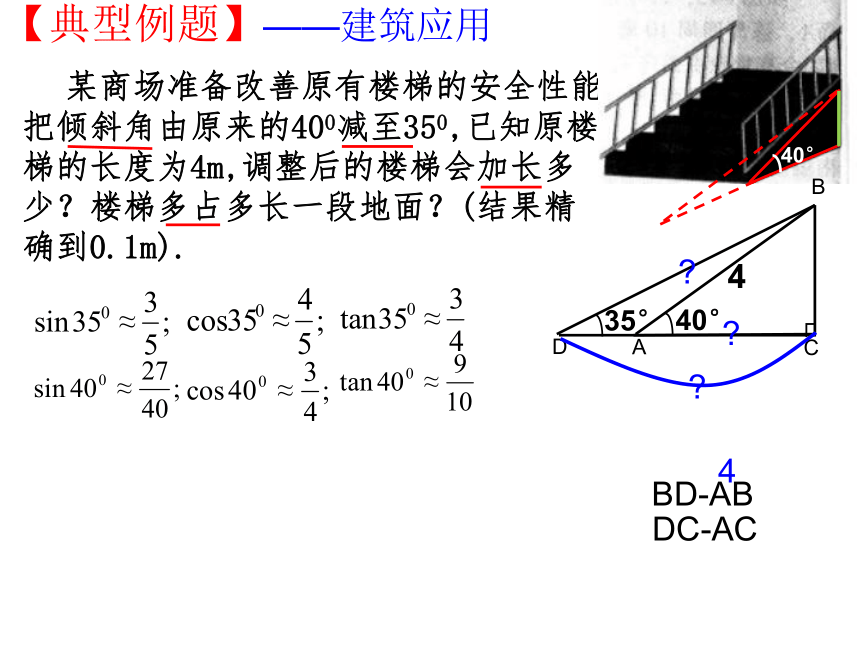
某商场准备改善原有楼梯的安全性能,把倾斜角由原来的400减至350,已知原楼梯的长度为4m,调整后的楼梯会加长多少?楼梯多占多长一段地面?(结果精确到0.1m).
【典型例题】——建筑应用
4
40°
BD-AB
DC-AC
4
?
?
?
D
B
C
A
┌
4
40°
35°
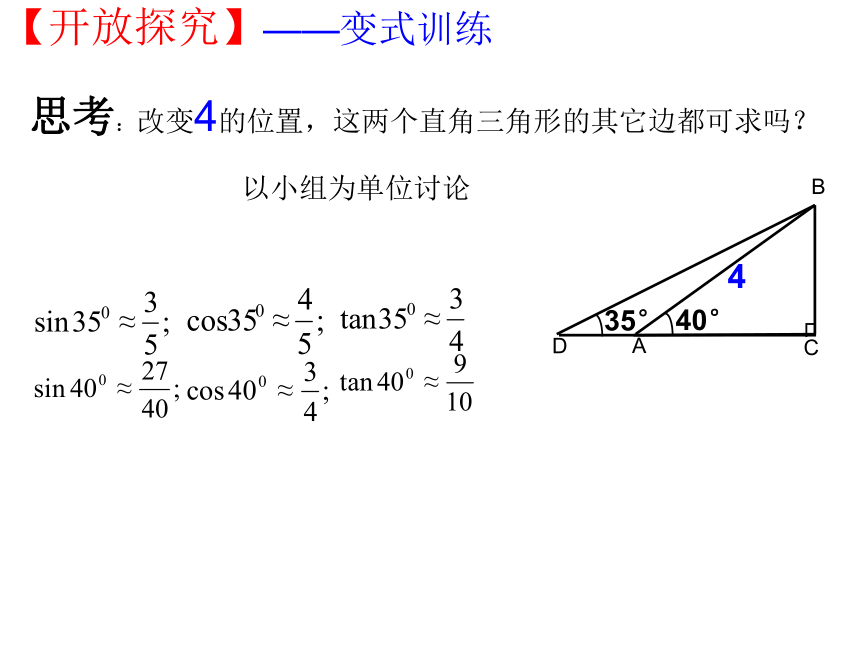
【开放探究】——变式训练
思考:改变4的位置,这两个直角三角形的其它边都可求吗?
以小组为单位讨论
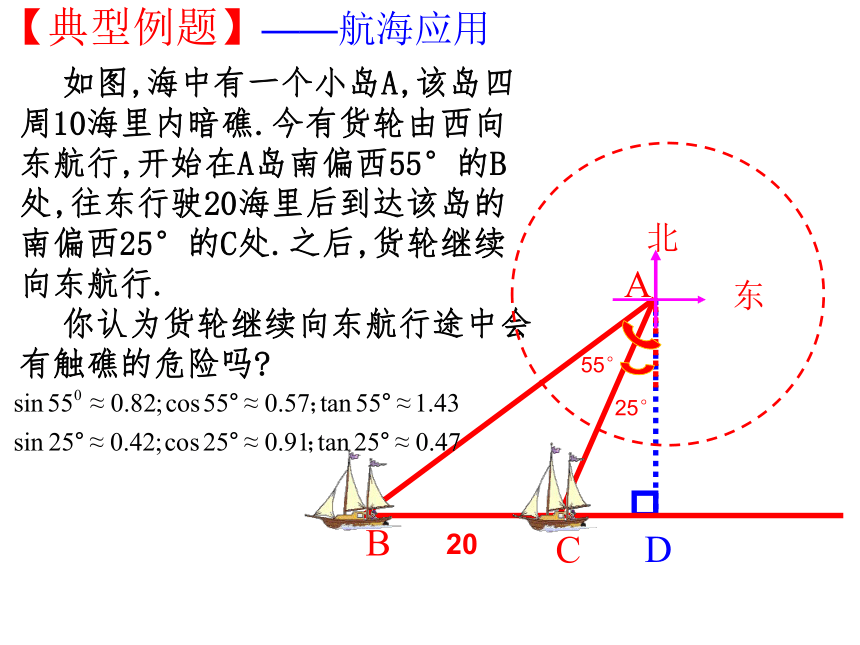
如图,海中有一个小岛A,该岛四周10海里内暗礁.今有货轮由西向东航行,开始在A岛南偏西55°的B处,往东行驶20海里后到达该岛的南偏西25°的C处.之后,货轮继续向东航行.
你认为货轮继续向东航行途中会有触礁的危险吗?
【典型例题】——航海应用
A
B
C
D
55°
25°
20
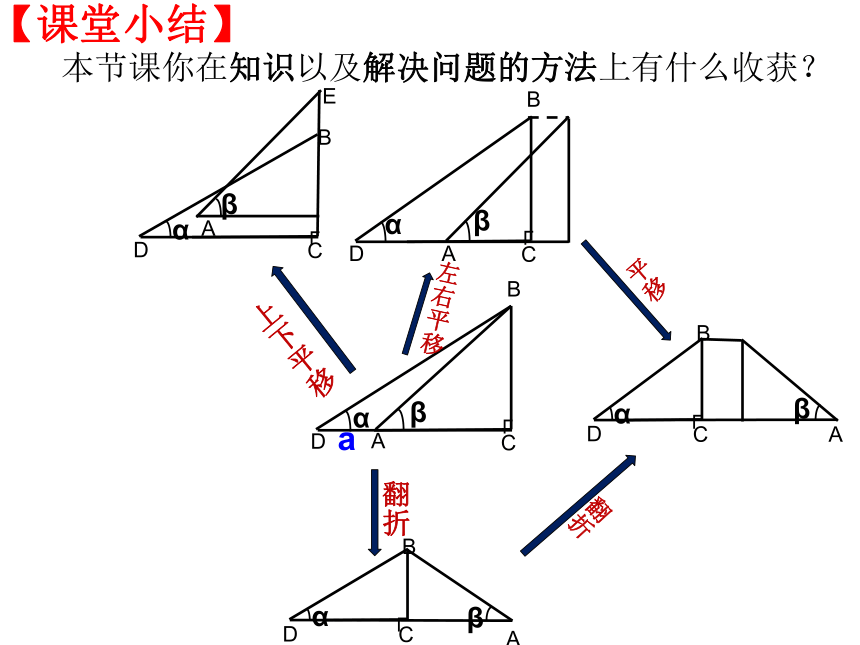
【课堂小结】
本节课你在知识以及解决问题的方法上有什么收获?
左右平移
上下平移
翻折
翻折
平移
【课堂小结】
本节课你在知识以及解决问题的方法上有什么收获?
乐学善思!
【布置作业】
必做:1.课本:P19 想一想
2.课本:P21 习题1.6 4
选做:三角函数在建筑设计、航海、国防、天气预报等方面都有广泛的应用,请查阅资料,了解“三角学”的发展史及应用.
为了测量河流某一段的宽度,在河北岸选了一点P,在河南岸选相距200米的A、B两点,分别测得∠PAB=42°,∠PBA=65°.要求这段河的宽度,若设河宽PC为x米,可列方程_________________.
【快速反应】
x
某商场准备改善原有楼梯的安全性能,把倾角由原来的400减至350,已知原楼梯的长度为4m,调整后的楼梯会加长多少?楼梯多占多长一段地面?(结果精确到0.01m).
【典型例题】 ——建筑应用
如图,海中有一个小岛A,该岛四周10海里内暗礁.今有货轮四由西向东航行,开始在A岛南偏西55°的B处,往东行驶20海里后到达该岛的南偏西25°的C处.之后,货轮继续向东航行.
请与同伴交流你是怎么想的? 怎么去做?
你认为货轮继续向东航行途中会有触礁的危险吗?
现在你能完成这个任务吗
某日在我国钓鱼岛附近海域有两艘自西向东航行的海监船A、B,B船在A船的正东方向,且两船保持20海里的距离,某一时刻两海监船同时测得在A的东北方向,B的北偏东15°方向有一我国渔政执法船C,求此时船C与船B的距离是多少(结果保留根号).
大展身手:
解析:
解直角三角形的知识点纵向分布较多,知识综合考查点为解直角三角形的应用——构造 ,通过边、方位角的关系,利用 直角三角形的 设未知数构建 解决实际问题。
中考小帮手:
实际问题
数学问题
弄清题意
计算求解
分析解题方法
构建直角三角形
代数方法
设未知数列方程
画出图形
知识小结:
解决问题
1.5三角函数的应用
1、直角三角形中各角之间的关系:
温故知新:
2、直角三角形中各边之间的关系:
3、直角三角形中边与角的关系:
4、解直角三角形需要哪些条件?
【自主梳理】
1.温情提示:
仰角、俯角:当从低处观测高处的目标时,视线与水平线所成的锐角称为仰角;当从高处观测低处的目标时,视线与水平线所成的锐角称为俯角.如图,∠1为仰角,∠2为俯角.
视线在水平线以上时,在视线所在的垂直平面内,视线与水平线所成的角叫做仰角. 俯角:在竖直面内的水平线与向下递降线段之间的角度(朝下看时,视线与水平面夹角为俯角)? 两者的范围都是0°到180°.
方位角:一般是指以观测者的位置为中心,将正北或正南方向作为起始方向旋转到目标的方向线所成的角(一般指锐角),通常表达成北(南)偏东(西)××度.如图,点A在点O的北偏东60°方向上,则点B在点O的南偏东45°方向上,此时,也可以说点B在点O的东南方向上.
2.请分别在三个图形中,用所给边和∠α表示其他两边
学习目标:
利用三角函数把实际问题转化为数学问题,进行有关三角函数的计算,并能对结果的意义进行说明。
某商场准备改善原有楼梯的安全性能,把倾斜角由原来的400减至350,已知原楼梯的长度为4m,调整后的楼梯会加长多少?楼梯多占多长一段地面?(结果精确到0.1m).
【典型例题】——建筑应用
4
40°
BD-AB
DC-AC
4
?
?
?
D
B
C
A
┌
4
40°
35°
【开放探究】——变式训练
思考:改变4的位置,这两个直角三角形的其它边都可求吗?
以小组为单位讨论
如图,海中有一个小岛A,该岛四周10海里内暗礁.今有货轮由西向东航行,开始在A岛南偏西55°的B处,往东行驶20海里后到达该岛的南偏西25°的C处.之后,货轮继续向东航行.
你认为货轮继续向东航行途中会有触礁的危险吗?
【典型例题】——航海应用
A
B
C
D
55°
25°
20
【课堂小结】
本节课你在知识以及解决问题的方法上有什么收获?
左右平移
上下平移
翻折
翻折
平移
【课堂小结】
本节课你在知识以及解决问题的方法上有什么收获?
乐学善思!
【布置作业】
必做:1.课本:P19 想一想
2.课本:P21 习题1.6 4
选做:三角函数在建筑设计、航海、国防、天气预报等方面都有广泛的应用,请查阅资料,了解“三角学”的发展史及应用.
为了测量河流某一段的宽度,在河北岸选了一点P,在河南岸选相距200米的A、B两点,分别测得∠PAB=42°,∠PBA=65°.要求这段河的宽度,若设河宽PC为x米,可列方程_________________.
【快速反应】
x
某商场准备改善原有楼梯的安全性能,把倾角由原来的400减至350,已知原楼梯的长度为4m,调整后的楼梯会加长多少?楼梯多占多长一段地面?(结果精确到0.01m).
【典型例题】 ——建筑应用
如图,海中有一个小岛A,该岛四周10海里内暗礁.今有货轮四由西向东航行,开始在A岛南偏西55°的B处,往东行驶20海里后到达该岛的南偏西25°的C处.之后,货轮继续向东航行.
请与同伴交流你是怎么想的? 怎么去做?
你认为货轮继续向东航行途中会有触礁的危险吗?
现在你能完成这个任务吗
某日在我国钓鱼岛附近海域有两艘自西向东航行的海监船A、B,B船在A船的正东方向,且两船保持20海里的距离,某一时刻两海监船同时测得在A的东北方向,B的北偏东15°方向有一我国渔政执法船C,求此时船C与船B的距离是多少(结果保留根号).
大展身手:
解析:
解直角三角形的知识点纵向分布较多,知识综合考查点为解直角三角形的应用——构造 ,通过边、方位角的关系,利用 直角三角形的 设未知数构建 解决实际问题。
中考小帮手:
实际问题
数学问题
弄清题意
计算求解
分析解题方法
构建直角三角形
代数方法
设未知数列方程
画出图形
知识小结:
解决问题
