三年级上册数学一课一练-数学好玩 2.搭配中的学问 北师大版(含答案)
文档属性
| 名称 | 三年级上册数学一课一练-数学好玩 2.搭配中的学问 北师大版(含答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 49.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-30 00:00:00 | ||
图片预览



文档简介
三年级上册数学一课一练-数学好玩 2.搭配中的学问
一、单选题
1.数一数如图中有( )条线段.
A.?1条??????????????????????????????????????B.?4条??????????????????????????????????????C.?9条??????????????????????????????????????D.?10条
2.高速公路入口处收费站有1号2号3号4号共四个收费窗口,有A,B,C三辆轿车要通过收费窗口购票入高速公路.那么,这三辆轿车共有( )种不同的购票次序.
A.?24????????????????????????????????????????B.?48????????????????????????????????????????C.?72????????????????????????????????????????D.?120
3.有8级台阶,小明从下向上走,若每次只能跨过一级或两级,他走上去可能有( )种不同方法.
A.?12?????????????????????????????????????????B.?24?????????????????????????????????????????C.?34?????????????????????????????????????????D.?36
4.一个密码锁由五个数字组成,每一位数字都是0~9之中的一个,小春只记得其中的三个,则他最多试(??? )次就能打开锁。
A.?5?????????????????????????????????????????B.?2?????????????????????????????????????????C.?20?????????????????????????????????????????D.?100
二、判断题
5.2件上衣和3条裤子搭配成一件衣服,一共有5种搭配方法(??? )
6.用 组成的最大三位数是682.
7.从5、2、7、0这4个数中选出两个组成两位数,可以组成9个两位数。
三、填空题
8.一只西瓜竖直切9刀,最多可切________?块.
9.妈妈看中不同款式的3件上衣和4条裤子,如果她要买一件上衣和一条裤子,她有________种买法。
10.要从5名女生和3名男生中各选出一名选手参加乒乓球男女混合双打,共有________种不同的选法.
11.学校开展体育比赛活动,六年级,8个班进行小小足球赛,体育老师把他们平均分成2个小组进行单循环比赛.
(1)每个班在小组内赛了________场.
(2)每个小组一共进行了________场比赛.
四、解答题
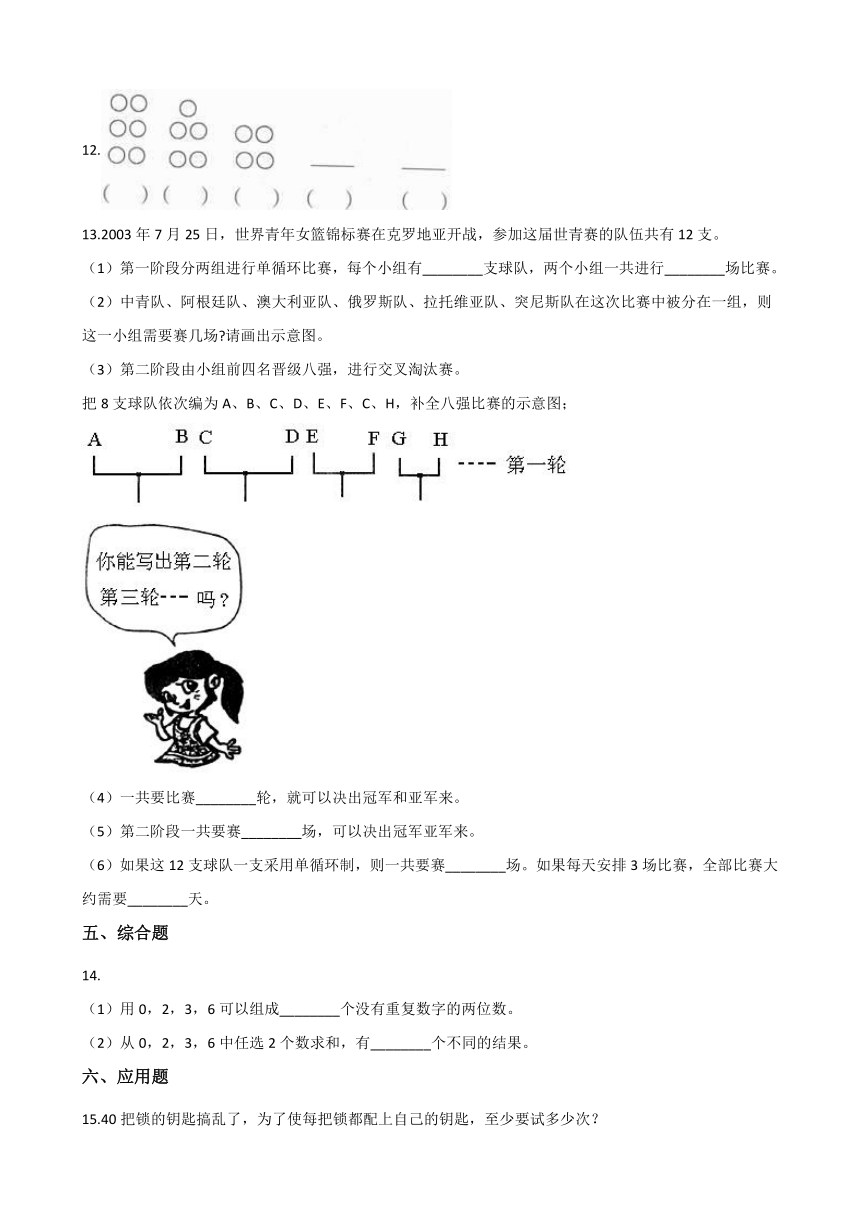
12.
13.2003年7月25日,世界青年女篮锦标赛在克罗地亚开战,参加这届世青赛的队伍共有12支。
(1)第一阶段分两组进行单循环比赛,每个小组有________支球队,两个小组一共进行________场比赛。
(2)中青队、阿根廷队、澳大利亚队、俄罗斯队、拉托维亚队、突尼斯队在这次比赛中被分在一组,则这一小组需要赛几场?请画出示意图。
(3)第二阶段由小组前四名晋级八强,进行交叉淘汰赛。
把8支球队依次编为A、B、C、D、E、F、C、H,补全八强比赛的示意图;
(4)一共要比赛________轮,就可以决出冠军和亚军来。
(5)第二阶段一共要赛________场,可以决出冠军亚军来。
(6)如果这12支球队一支采用单循环制,则一共要赛________场。如果每天安排3场比赛,全部比赛大约需要________天。
五、综合题
14.??
(1)用0,2,3,6可以组成________个没有重复数字的两位数。
(2)从0,2,3,6中任选2个数求和,有________个不同的结果。
六、应用题
15.40把锁的钥匙搞乱了,为了使每把锁都配上自己的钥匙,至少要试多少次?
参考答案
一、单选题
1.【答案】 D
【解析】【解答】解:根据题意,这条线上的5个点,它的组合情况是:
5×4÷2=20÷2=10(条);
答:图中一共有10条线段.
故选:D.
【分析】这条线上一共有5个点,每两个点都可以组成一条线段,一共有5×4种排列情况,又由于每两个点都重复了一次,比如AB和BA就是同一条线段,所以这条线上的5个点,一共有5×4÷2种组合.
2.【答案】 C
【解析】【解答】解:分三步进行:
第一步先确定A:A车有4个窗口可以选择;
第二步确定B:
因为B车可以在A车前也可以在A车之后,或者其他三个还没有缴费的窗口,一共有5种可能.
B车有2+3=5种选择;
第三步确定C:
因为不管前面的A和B车是在同一个缴费口还是在两个不同的缴费口分别缴费的情况,C都有6种方法安排.
比如前面A、B两车都在1号,再比如是按照A、B的顺序排的,这个时候2、3、4都是空的,那么C车可以在A前面,在A和B之间,或者是在B之后,或者是在2、3、4号,所以这个时候C就有3+3=6种安排方法.或者A、B车在前面两个不同的窗口缴费如在1号和2号缴费的,那么C车可以选择在号的A前或者A之后2种,B车之前或者B车之后2种,或者3号或者4号共2种,
那么C车也有2+2+1+1=6种方法.
所以三个车缴费的方法就有
4×5×6=120种方法.
故选:C.
【分析】分步计数,A有4种不同的购票窗口,B车可以在A车前也可以在A车之后,或者其他三个还没有缴费的窗口,一共有5种可能;同理得出C的方法,然后把它们相乘即可求解 .
3.【答案】 C
【解析】【解答】解:根据分析可得,
1+1=2,
1+2=3,
2+3=5,
3+5=8,
5+8=13,
13+8=21,
13+21=34;
答:他走上去可能有34种不同方法.
故选:C.
【分析】走一阶有1种方法,走2阶有2种方法,走3阶有3种方法,4走阶有5种方法,…然后可得出规律:从走3阶开始,每次是前面两阶的和,据此解答.
4.【答案】 D
【解析】【解答】解:10×10=100,最多试100次就能打开锁. 故答案为:D
【分析】因为只记得3个,还有2个数字不知道,因此需要把这两个数字都试完,每个数字都有10个数字可以选择,共10×10=100种情况,因此需要把这100种情况都试完才能保证打开锁.
二、判断题
5.【答案】 正确
【解析】【解答】解:一共有2×3=6种搭配方法。 故答案为:正确。 【分析】一件上衣有3种搭配裤子的方法,那么2件上衣就有2×3=6种搭配方法。
6.【答案】 错误
【解析】【解答】 用 组成的最大三位数是862,原题说法错误。 故答案为:错误。
【分析】根据题意可知,要求用三张不同的数字卡片组成最大的三位数,将这三个数字按从大到小的顺序排列即可。
7.【答案】 正确
【解析】【解答】 从5、2、7、0这4个数中选出两个组成两位数,可以组成9个两位数:50、52、57、20、25、27、70、72、75,原题说法正确. 故答案为:正确.
【分析】根据题意可知,4个数中除0之外,其他三个数都可以先放在十位上,十位上有3种不同情况;当十位数字确定后,个位数字也有3种不同的情况,一共可以组成3×3=9个两位数,据此判断.
三、填空题
8.【答案】46
【解析】【解答】解:当切1刀时,块数为:1+1=2(块); 当切2刀时,块数为:1+1+2=4(块); 当切3刀时,块数为:1+1+2+3=7(块); … 当切n刀时,块数:1+(1+2+3…+n). 则切9刀时,块数为:1+1+2+3+4+5+6+7+8+9=46(块). 故答案为:46. 【分析】由题意可知:当切1刀时,块数为1+1=2块;当切2刀时,块数为1+1+2=4块;当切3刀时,块数为1+1+2+3=7块;当切4刀时,块数为1+1+2+3+4=11块;当切5刀时,块数为1+1+2+3+4+5=16块;… 继而可得出切n刀时所得的块数,进一步代入求得答案即可.
9.【答案】 12
【解析】【解答】3×4=12(种) 故答案为:12。 【分析】此题主要考查了排列和组合的知识,每件上衣可以搭配4条不同的裤子,那么3件上衣就可以搭配3×4=12种不同的买法。
10.【答案】15
【解析】【解答】5×3=15(种) 故答案为:15 【分析】因为有3名男生,那么1名女生会有3种不同的组合;共有5名女生,就会有5个3种不同的选择,因此用乘法计算即可.
11.【答案】(1)3.
(2)6.
【解析】【解答】解:(1)1.8÷2=4(个) 4-1=3(场) (2)4×3÷2=6(场) 故答案为:3,6。 【分析】1。用8除以2求出每个小组的班数是4个班,每个班与其他3个班进行比赛时都要赛3场,据此解答即可;因为每个小组有4个班,每个班与其他班进行比赛时都要赛3场,用4乘3计算比赛场次时有一半重复的,所以再除以2即可。
四、解答题
12.【答案】
【解析】
13.【答案】(1)6 ;30 (2)15 (3) (4)三 (5)两 (6)66;22
【解析】【分析】本题直接根据排列组合的方法进行解答即可。
五、综合题
14.【答案】 (1)9 (2)6
【解析】【解答】解:(1)用0,2,3,6可以组成9个没有重复数字的两位数;(2)从0,2,3,6中任选2个数求和,有6个不同的结果。 故答案为:(1)9;(2)6。 【分析】(1)0,2,3,6可以组成没有重复数字的两位数有:20、30、60、32、62、13、63、26、36,一共9个; (2)从0,2,3,6中任选2个数求和,0+2=2,0+3=3,0+6=6,2+3=5,2+6=8,3+6=7,一共有6中不同的结果。
六、应用题
15.【答案】解:39+38+37+…+1 =(39+1)×39÷2 =40×39÷2 =780(次) 答:至少要试780次
【解析】【分析】从最差情况考虑:要确保锁和钥匙都配对起来,开第一把锁,试了39次都没有打开,第40把钥匙就不需要试了,肯定配这把锁的.同理,开第二把锁时,最多就需要38次,以此类推…第39把锁最多需要试1次,第40把锁就不需要试了,剩下的最后一把钥匙就一定是配这把锁的了.所以最多需要(39+38+37+…+1)次.
一、单选题
1.数一数如图中有( )条线段.
A.?1条??????????????????????????????????????B.?4条??????????????????????????????????????C.?9条??????????????????????????????????????D.?10条
2.高速公路入口处收费站有1号2号3号4号共四个收费窗口,有A,B,C三辆轿车要通过收费窗口购票入高速公路.那么,这三辆轿车共有( )种不同的购票次序.
A.?24????????????????????????????????????????B.?48????????????????????????????????????????C.?72????????????????????????????????????????D.?120
3.有8级台阶,小明从下向上走,若每次只能跨过一级或两级,他走上去可能有( )种不同方法.
A.?12?????????????????????????????????????????B.?24?????????????????????????????????????????C.?34?????????????????????????????????????????D.?36
4.一个密码锁由五个数字组成,每一位数字都是0~9之中的一个,小春只记得其中的三个,则他最多试(??? )次就能打开锁。
A.?5?????????????????????????????????????????B.?2?????????????????????????????????????????C.?20?????????????????????????????????????????D.?100
二、判断题
5.2件上衣和3条裤子搭配成一件衣服,一共有5种搭配方法(??? )
6.用 组成的最大三位数是682.
7.从5、2、7、0这4个数中选出两个组成两位数,可以组成9个两位数。
三、填空题
8.一只西瓜竖直切9刀,最多可切________?块.
9.妈妈看中不同款式的3件上衣和4条裤子,如果她要买一件上衣和一条裤子,她有________种买法。
10.要从5名女生和3名男生中各选出一名选手参加乒乓球男女混合双打,共有________种不同的选法.
11.学校开展体育比赛活动,六年级,8个班进行小小足球赛,体育老师把他们平均分成2个小组进行单循环比赛.
(1)每个班在小组内赛了________场.
(2)每个小组一共进行了________场比赛.
四、解答题
12.
13.2003年7月25日,世界青年女篮锦标赛在克罗地亚开战,参加这届世青赛的队伍共有12支。
(1)第一阶段分两组进行单循环比赛,每个小组有________支球队,两个小组一共进行________场比赛。
(2)中青队、阿根廷队、澳大利亚队、俄罗斯队、拉托维亚队、突尼斯队在这次比赛中被分在一组,则这一小组需要赛几场?请画出示意图。
(3)第二阶段由小组前四名晋级八强,进行交叉淘汰赛。
把8支球队依次编为A、B、C、D、E、F、C、H,补全八强比赛的示意图;
(4)一共要比赛________轮,就可以决出冠军和亚军来。
(5)第二阶段一共要赛________场,可以决出冠军亚军来。
(6)如果这12支球队一支采用单循环制,则一共要赛________场。如果每天安排3场比赛,全部比赛大约需要________天。
五、综合题
14.??
(1)用0,2,3,6可以组成________个没有重复数字的两位数。
(2)从0,2,3,6中任选2个数求和,有________个不同的结果。
六、应用题
15.40把锁的钥匙搞乱了,为了使每把锁都配上自己的钥匙,至少要试多少次?
参考答案
一、单选题
1.【答案】 D
【解析】【解答】解:根据题意,这条线上的5个点,它的组合情况是:
5×4÷2=20÷2=10(条);
答:图中一共有10条线段.
故选:D.
【分析】这条线上一共有5个点,每两个点都可以组成一条线段,一共有5×4种排列情况,又由于每两个点都重复了一次,比如AB和BA就是同一条线段,所以这条线上的5个点,一共有5×4÷2种组合.
2.【答案】 C
【解析】【解答】解:分三步进行:
第一步先确定A:A车有4个窗口可以选择;
第二步确定B:
因为B车可以在A车前也可以在A车之后,或者其他三个还没有缴费的窗口,一共有5种可能.
B车有2+3=5种选择;
第三步确定C:
因为不管前面的A和B车是在同一个缴费口还是在两个不同的缴费口分别缴费的情况,C都有6种方法安排.
比如前面A、B两车都在1号,再比如是按照A、B的顺序排的,这个时候2、3、4都是空的,那么C车可以在A前面,在A和B之间,或者是在B之后,或者是在2、3、4号,所以这个时候C就有3+3=6种安排方法.或者A、B车在前面两个不同的窗口缴费如在1号和2号缴费的,那么C车可以选择在号的A前或者A之后2种,B车之前或者B车之后2种,或者3号或者4号共2种,
那么C车也有2+2+1+1=6种方法.
所以三个车缴费的方法就有
4×5×6=120种方法.
故选:C.
【分析】分步计数,A有4种不同的购票窗口,B车可以在A车前也可以在A车之后,或者其他三个还没有缴费的窗口,一共有5种可能;同理得出C的方法,然后把它们相乘即可求解 .
3.【答案】 C
【解析】【解答】解:根据分析可得,
1+1=2,
1+2=3,
2+3=5,
3+5=8,
5+8=13,
13+8=21,
13+21=34;
答:他走上去可能有34种不同方法.
故选:C.
【分析】走一阶有1种方法,走2阶有2种方法,走3阶有3种方法,4走阶有5种方法,…然后可得出规律:从走3阶开始,每次是前面两阶的和,据此解答.
4.【答案】 D
【解析】【解答】解:10×10=100,最多试100次就能打开锁. 故答案为:D
【分析】因为只记得3个,还有2个数字不知道,因此需要把这两个数字都试完,每个数字都有10个数字可以选择,共10×10=100种情况,因此需要把这100种情况都试完才能保证打开锁.
二、判断题
5.【答案】 正确
【解析】【解答】解:一共有2×3=6种搭配方法。 故答案为:正确。 【分析】一件上衣有3种搭配裤子的方法,那么2件上衣就有2×3=6种搭配方法。
6.【答案】 错误
【解析】【解答】 用 组成的最大三位数是862,原题说法错误。 故答案为:错误。
【分析】根据题意可知,要求用三张不同的数字卡片组成最大的三位数,将这三个数字按从大到小的顺序排列即可。
7.【答案】 正确
【解析】【解答】 从5、2、7、0这4个数中选出两个组成两位数,可以组成9个两位数:50、52、57、20、25、27、70、72、75,原题说法正确. 故答案为:正确.
【分析】根据题意可知,4个数中除0之外,其他三个数都可以先放在十位上,十位上有3种不同情况;当十位数字确定后,个位数字也有3种不同的情况,一共可以组成3×3=9个两位数,据此判断.
三、填空题
8.【答案】46
【解析】【解答】解:当切1刀时,块数为:1+1=2(块); 当切2刀时,块数为:1+1+2=4(块); 当切3刀时,块数为:1+1+2+3=7(块); … 当切n刀时,块数:1+(1+2+3…+n). 则切9刀时,块数为:1+1+2+3+4+5+6+7+8+9=46(块). 故答案为:46. 【分析】由题意可知:当切1刀时,块数为1+1=2块;当切2刀时,块数为1+1+2=4块;当切3刀时,块数为1+1+2+3=7块;当切4刀时,块数为1+1+2+3+4=11块;当切5刀时,块数为1+1+2+3+4+5=16块;… 继而可得出切n刀时所得的块数,进一步代入求得答案即可.
9.【答案】 12
【解析】【解答】3×4=12(种) 故答案为:12。 【分析】此题主要考查了排列和组合的知识,每件上衣可以搭配4条不同的裤子,那么3件上衣就可以搭配3×4=12种不同的买法。
10.【答案】15
【解析】【解答】5×3=15(种) 故答案为:15 【分析】因为有3名男生,那么1名女生会有3种不同的组合;共有5名女生,就会有5个3种不同的选择,因此用乘法计算即可.
11.【答案】(1)3.
(2)6.
【解析】【解答】解:(1)1.8÷2=4(个) 4-1=3(场) (2)4×3÷2=6(场) 故答案为:3,6。 【分析】1。用8除以2求出每个小组的班数是4个班,每个班与其他3个班进行比赛时都要赛3场,据此解答即可;因为每个小组有4个班,每个班与其他班进行比赛时都要赛3场,用4乘3计算比赛场次时有一半重复的,所以再除以2即可。
四、解答题
12.【答案】
【解析】
13.【答案】(1)6 ;30 (2)15 (3) (4)三 (5)两 (6)66;22
【解析】【分析】本题直接根据排列组合的方法进行解答即可。
五、综合题
14.【答案】 (1)9 (2)6
【解析】【解答】解:(1)用0,2,3,6可以组成9个没有重复数字的两位数;(2)从0,2,3,6中任选2个数求和,有6个不同的结果。 故答案为:(1)9;(2)6。 【分析】(1)0,2,3,6可以组成没有重复数字的两位数有:20、30、60、32、62、13、63、26、36,一共9个; (2)从0,2,3,6中任选2个数求和,0+2=2,0+3=3,0+6=6,2+3=5,2+6=8,3+6=7,一共有6中不同的结果。
六、应用题
15.【答案】解:39+38+37+…+1 =(39+1)×39÷2 =40×39÷2 =780(次) 答:至少要试780次
【解析】【分析】从最差情况考虑:要确保锁和钥匙都配对起来,开第一把锁,试了39次都没有打开,第40把钥匙就不需要试了,肯定配这把锁的.同理,开第二把锁时,最多就需要38次,以此类推…第39把锁最多需要试1次,第40把锁就不需要试了,剩下的最后一把钥匙就一定是配这把锁的了.所以最多需要(39+38+37+…+1)次.
同课章节目录
