2.2.1 一次函数的性质与图象
文档属性
| 名称 | 2.2.1 一次函数的性质与图象 |

|
|
| 格式 | zip | ||
| 文件大小 | 598.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-04 00:00:00 | ||
图片预览




文档简介
课件19张PPT。2.2.1一次函数的图象和性质1、一次函数的概念问题1 在初中我们学习过一次 函数 ,那么一次函数是如何定义的?
定义域是什么?值域是什么?问题2 一次函数的图象是什么,
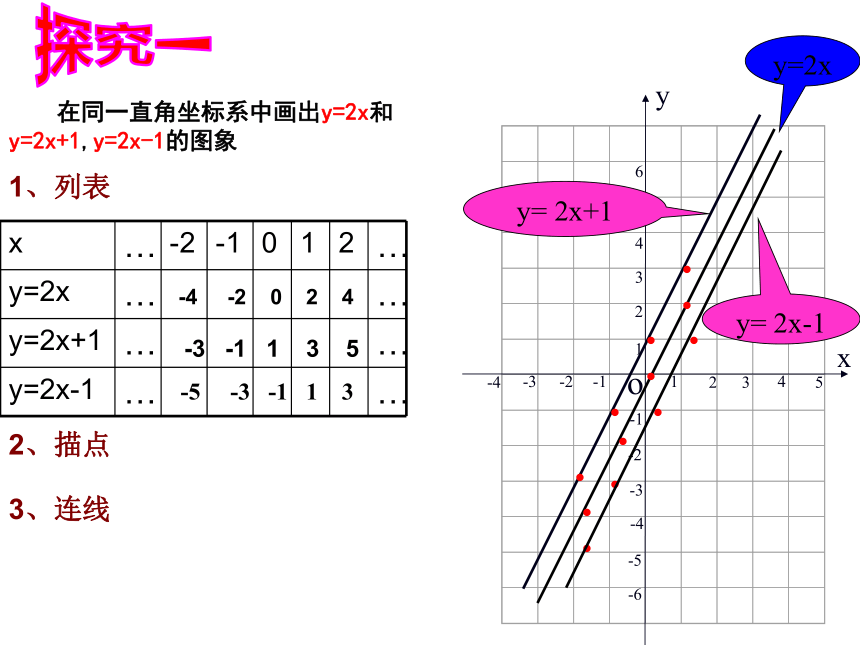
表达式中的k,b的几何意义又是什么?2、一次函数的图象与性质:思考1:提出研究函数性质的内容和方法研究方法:画出函数的图象,结合图象研究函数的性质。研究内容:定义域 值域 图象 单调性 奇偶性 思考2:如何画一次函数的图象呢?列表、描点、连线 -4 -2 0 2 4 在同一直角坐标系中画出y=2x和
y=2x+1,y=2x-1的图象1、列表······2、描点3、连线y=2xy= 2x+1探究一······ -3 -1 1 3 5 -5 -3 -1 1 3y= 2x-1观察得出:
1.一次函数y = kx + b的图象也是一条_____,
我们称它是______________,所以今后只需
选取_____个点即可画出图象.
2.这三条直线互相_______,
直线y= 2x+1是由直线y= 2x向____平移____个单位长度得来的,
直线y= 2x-1是由直线y= 2x向____平移____个单位长度得来的.
3.直线y= 2x+1与y轴交于点______,
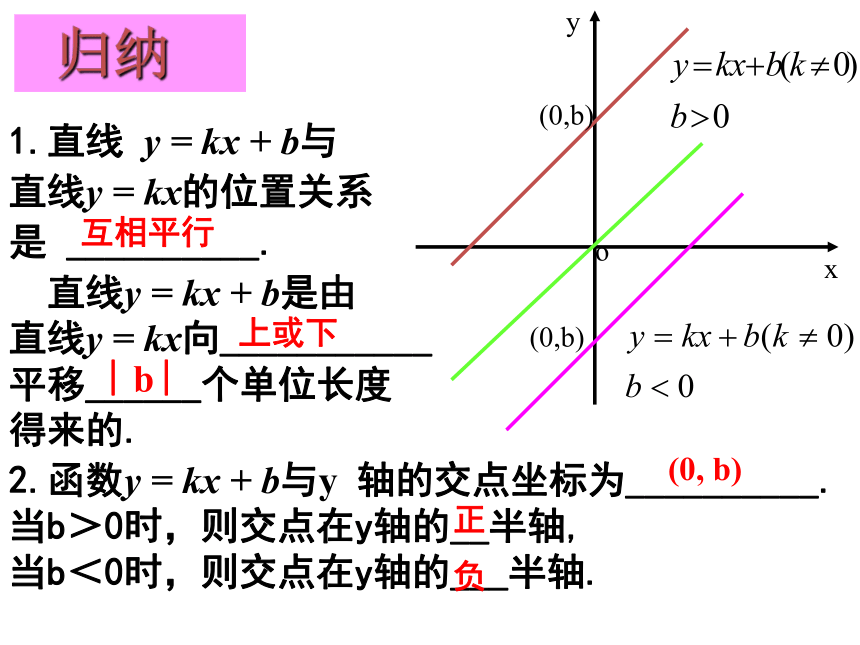
直线y= 2x-1与y轴交于点______.平行上1下1(0,1)(0,-1)直线直线y = kx + b两y=2xy=2x+1 归纳1.直线 y = kx + b与
直线y = kx的位置关系
是 __________.互相平行
2.函数y = kx + b与y 轴的交点坐标为__________.
当b>0时,则交点在y轴的__半轴,
当b<0时,则交点在y轴的___半轴.
(0, b) 直线y = kx + b是由
直线y = kx向___________
平移______个单位长度
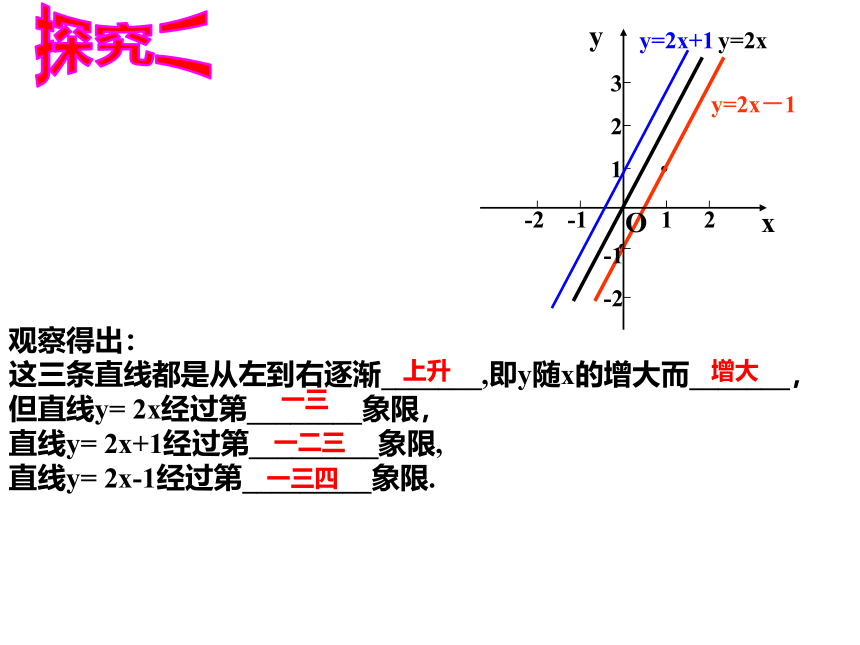
得来的.上或下︱b ︳正负y=2xy=2x+1探究二观察得出:
这三条直线都是从左到右逐渐_______,即y随x的增大而_______,
但直线y= 2x经过第________象限,
直线y= 2x+1经过第_________象限,
直线y= 2x-1经过第_________象限.上升增大一三一二三一三四
探究二观察得出:
这三条直线都是从左到右逐渐_______,即y随x的增大而_____,
但直线y= -x经过第________象限,
直线y= -x+4经过第_________象限,
直线y= -x-4经过第_________象限.请在同一直角坐标系中作y=-x和y=-x+4,y=-x-4的图象
··y=-x+44-4-3 -2 -1 1 2 3 4123··-4y=-x-4y=-x探究二··观察得出:
这三条直线都是从左到右逐渐_______,即y随x的增大而_____,
但直线y= -x经过第________象限,
直线y= -x+4经过第_________象限,
直线y= -x-4经过第_________象限.下降二四一二四二三四减小一次函数y=kx+b(k≠0)的性质:当______时,图象从左
到右逐渐______,y随x的
增大而______.y=2x-1当______时,图象从左
到右逐渐______,y随x的
增大而______.xyoy=-x+4y=-xy=-x-4k>0k<0上升下降增大减小与k有关与k有关
试证明一次函数的单调性试判断一次函数的奇偶性一、二、三一、三、四一、二、四二、三、四k>0
b>0k>0
b<0k<0
b>0k<0
b<0奇偶性b=0 奇函数
b≠0 既不是奇函数也不是偶函数增函数增函数减函数减函数一次函数的图象和性质1、有下列函数:①y=2x+1, ②y=-3x+4,
③ y=0.5x, ④y=x-6;①3 ④②③①函数y随x的增大而增大的是__________;其中过原点的直线是________;函数y随x的增大而减小的是___________;图象在第一、二、三象限的是________ 。练
一
练yxyx0
逆向思维 小试牛刀
2、已知函数 y = kx的图象在二、四象限,那么函数y = kx-k的图象可能是( )B 3、已知一次函数y = mx-(m-2),
若它的图象经过原点,则 m= ;
若点(0 ,3) 在它的图象上,则m = ;若它的图象经过一、二、四象限,则m .2-1<0
1、已知一次函数 y=(1-2m)x+m-1 , 求满足下列条件的m的值:
(1)函数值y 随x的增大而增大;
(2)函数图象与y 轴的负半轴相交;
(3)函数的图象过第二、三、四象限;
(4)函数的图象过原点。摩拳擦掌大显身手 2. 对于一次函数y= x+3,
当1≤x≤4时, y的取值范围
是___________.y=-x+3,4≤y≤7-1≤y≤2y=x+3y=-x+3 当x>4时,
y____; < -1< 1当x____时, y>2.这节课你学到了什么?会画一次函数的图象一次函数的图象与性质,常
数k,b的意义和作用.体会数形结合的思想与方法进一步体验研究函数的一般思路与方法. 课堂小结作业:课后练习A组课堂检测: 1、 对于函数y=5x+6,y的值随x的值减小而______。 3、点A(-3,y1)、点B(2,y2)都在直线y=–4x+3上,
则y1与y2的关系是( )
A y1 ≤ y2 B y1 = y2 C y1< y2 D y1 >y24.一次函数 的图象与 y 轴的交点
坐标(0,1),且平行于直线 ,求这
个一次函数的解析式.
定义域是什么?值域是什么?问题2 一次函数的图象是什么,
表达式中的k,b的几何意义又是什么?2、一次函数的图象与性质:思考1:提出研究函数性质的内容和方法研究方法:画出函数的图象,结合图象研究函数的性质。研究内容:定义域 值域 图象 单调性 奇偶性 思考2:如何画一次函数的图象呢?列表、描点、连线 -4 -2 0 2 4 在同一直角坐标系中画出y=2x和
y=2x+1,y=2x-1的图象1、列表······2、描点3、连线y=2xy= 2x+1探究一······ -3 -1 1 3 5 -5 -3 -1 1 3y= 2x-1观察得出:
1.一次函数y = kx + b的图象也是一条_____,
我们称它是______________,所以今后只需
选取_____个点即可画出图象.
2.这三条直线互相_______,
直线y= 2x+1是由直线y= 2x向____平移____个单位长度得来的,
直线y= 2x-1是由直线y= 2x向____平移____个单位长度得来的.
3.直线y= 2x+1与y轴交于点______,
直线y= 2x-1与y轴交于点______.平行上1下1(0,1)(0,-1)直线直线y = kx + b两y=2xy=2x+1 归纳1.直线 y = kx + b与
直线y = kx的位置关系
是 __________.互相平行
2.函数y = kx + b与y 轴的交点坐标为__________.
当b>0时,则交点在y轴的__半轴,
当b<0时,则交点在y轴的___半轴.
(0, b) 直线y = kx + b是由
直线y = kx向___________
平移______个单位长度
得来的.上或下︱b ︳正负y=2xy=2x+1探究二观察得出:
这三条直线都是从左到右逐渐_______,即y随x的增大而_______,
但直线y= 2x经过第________象限,
直线y= 2x+1经过第_________象限,
直线y= 2x-1经过第_________象限.上升增大一三一二三一三四
探究二观察得出:
这三条直线都是从左到右逐渐_______,即y随x的增大而_____,
但直线y= -x经过第________象限,
直线y= -x+4经过第_________象限,
直线y= -x-4经过第_________象限.请在同一直角坐标系中作y=-x和y=-x+4,y=-x-4的图象
··y=-x+44-4-3 -2 -1 1 2 3 4123··-4y=-x-4y=-x探究二··观察得出:
这三条直线都是从左到右逐渐_______,即y随x的增大而_____,
但直线y= -x经过第________象限,
直线y= -x+4经过第_________象限,
直线y= -x-4经过第_________象限.下降二四一二四二三四减小一次函数y=kx+b(k≠0)的性质:当______时,图象从左
到右逐渐______,y随x的
增大而______.y=2x-1当______时,图象从左
到右逐渐______,y随x的
增大而______.xyoy=-x+4y=-xy=-x-4k>0k<0上升下降增大减小与k有关与k有关
试证明一次函数的单调性试判断一次函数的奇偶性一、二、三一、三、四一、二、四二、三、四k>0
b>0k>0
b<0k<0
b>0k<0
b<0奇偶性b=0 奇函数
b≠0 既不是奇函数也不是偶函数增函数增函数减函数减函数一次函数的图象和性质1、有下列函数:①y=2x+1, ②y=-3x+4,
③ y=0.5x, ④y=x-6;①3 ④②③①函数y随x的增大而增大的是__________;其中过原点的直线是________;函数y随x的增大而减小的是___________;图象在第一、二、三象限的是________ 。练
一
练yxyx0
逆向思维 小试牛刀
2、已知函数 y = kx的图象在二、四象限,那么函数y = kx-k的图象可能是( )B 3、已知一次函数y = mx-(m-2),
若它的图象经过原点,则 m= ;
若点(0 ,3) 在它的图象上,则m = ;若它的图象经过一、二、四象限,则m .2-1<0
1、已知一次函数 y=(1-2m)x+m-1 , 求满足下列条件的m的值:
(1)函数值y 随x的增大而增大;
(2)函数图象与y 轴的负半轴相交;
(3)函数的图象过第二、三、四象限;
(4)函数的图象过原点。摩拳擦掌大显身手 2. 对于一次函数y= x+3,
当1≤x≤4时, y的取值范围
是___________.y=-x+3,4≤y≤7-1≤y≤2y=x+3y=-x+3 当x>4时,
y____; < -1< 1当x____时, y>2.这节课你学到了什么?会画一次函数的图象一次函数的图象与性质,常
数k,b的意义和作用.体会数形结合的思想与方法进一步体验研究函数的一般思路与方法. 课堂小结作业:课后练习A组课堂检测: 1、 对于函数y=5x+6,y的值随x的值减小而______。 3、点A(-3,y1)、点B(2,y2)都在直线y=–4x+3上,
则y1与y2的关系是( )
A y1 ≤ y2 B y1 = y2 C y1< y2 D y1 >y24.一次函数 的图象与 y 轴的交点
坐标(0,1),且平行于直线 ,求这
个一次函数的解析式.
