3.1.1 实数指数幂及其运算 20张PPT
文档属性
| 名称 | 3.1.1 实数指数幂及其运算 20张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 339.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-05 09:43:29 | ||
图片预览




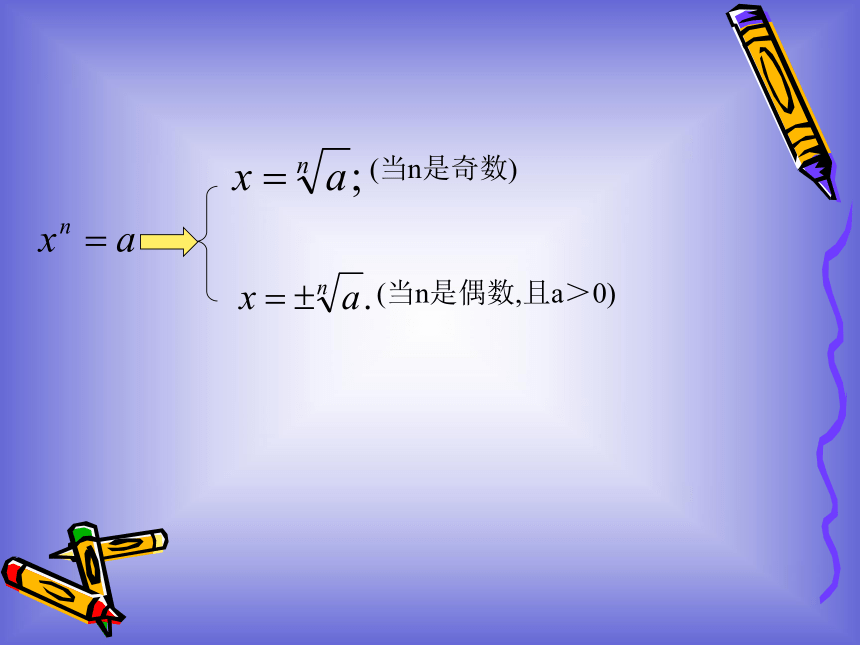



文档简介
课件20张PPT。实数指数幂
及其运算高中数学必修1 (新课标人教版)一 · 复习规定:
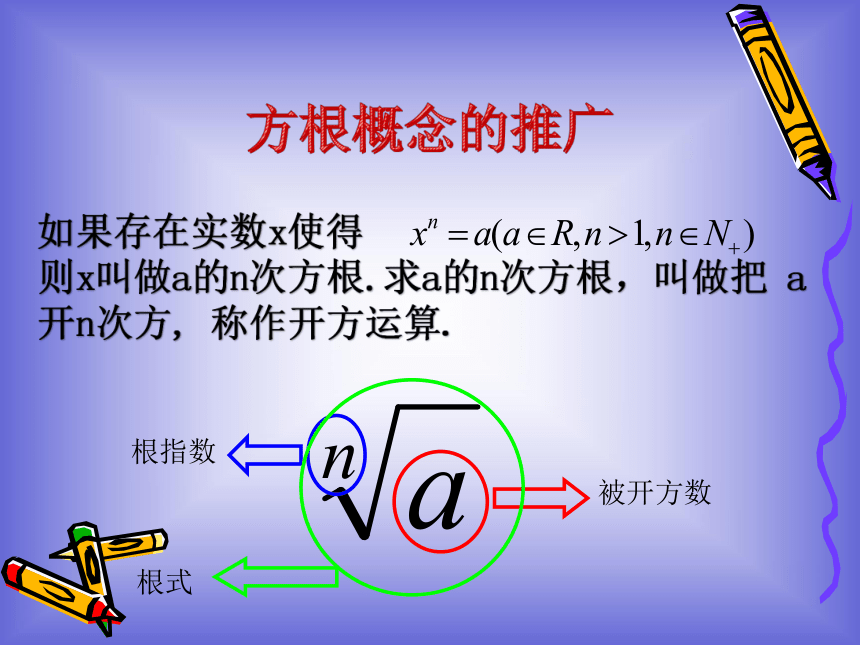
二、引入:平方根、立方根的概念22=4 (-2)2=4-2和2叫4 的平方根23=82叫8的立方根 (-2)3=-8-2叫-8的立方根25=322叫32的5次方根…………2叫a的n次方根2n=a方根概念的推广如果存在实数x使得 则x叫做a的n次方根.求a的n次方根,叫做把 a开n次方, 称作开方运算.被开方数根式n次方根 概念的理解(1)25的平方根是________
(2)27的立方根是________
(3) -32的五次方根是_____
(4)16的四次方根是_____
(5)a6的三次方根是________
(6)0的七次方根是________±53-2±2a203-23281观察发现分数指数幂=a=a2分析归纳:1.正分数指数幂2.负分数指数幂注意:分母是根指数注意:底数a>0这个条件不可少. 若无此条件会引起混乱,例如,(-1)1/3和(-1)2/6应当具有同样的意义,但由分数指数幂的意义可得出不同的结果:
=-1; =1. 这就说明分数指数幂在底数小于0时无意义.3.有理数指数幂运算法则:注:此运算法则对无理数指数幂同样适用。实数熟能生巧例1:计算幂的运算同样满足乘法公式及运算律。例2.计算例3.化简下列各式
快乐体验:1. 的值是( )2. 化简得( )3.下列各式中正确的是( )4.设 ,化简式子 AAD小结: ②指数概念的扩充,引入分数指数幂概念后,指数概念就实现了由整数指数幂向有理数指数幂的扩充,而且有理指数幂的运算性质对于无理指数幂也适用,这样指数概念就扩充到了整个实数范围。①分数指数幂的意义及运算性质 ③对于指数幂 ,当指数n扩大至有理数时,要注意底数a的变化范围。如当n=0时底数a≠0;当n为负整数指数时,底数a≠0;当n为分数时,底数a>0。
及其运算高中数学必修1 (新课标人教版)一 · 复习规定:
二、引入:平方根、立方根的概念22=4 (-2)2=4-2和2叫4 的平方根23=82叫8的立方根 (-2)3=-8-2叫-8的立方根25=322叫32的5次方根…………2叫a的n次方根2n=a方根概念的推广如果存在实数x使得 则x叫做a的n次方根.求a的n次方根,叫做把 a开n次方, 称作开方运算.被开方数根式n次方根 概念的理解(1)25的平方根是________
(2)27的立方根是________
(3) -32的五次方根是_____
(4)16的四次方根是_____
(5)a6的三次方根是________
(6)0的七次方根是________±53-2±2a203-23281观察发现分数指数幂=a=a2分析归纳:1.正分数指数幂2.负分数指数幂注意:分母是根指数注意:底数a>0这个条件不可少. 若无此条件会引起混乱,例如,(-1)1/3和(-1)2/6应当具有同样的意义,但由分数指数幂的意义可得出不同的结果:
=-1; =1. 这就说明分数指数幂在底数小于0时无意义.3.有理数指数幂运算法则:注:此运算法则对无理数指数幂同样适用。实数熟能生巧例1:计算幂的运算同样满足乘法公式及运算律。例2.计算例3.化简下列各式
快乐体验:1. 的值是( )2. 化简得( )3.下列各式中正确的是( )4.设 ,化简式子 AAD小结: ②指数概念的扩充,引入分数指数幂概念后,指数概念就实现了由整数指数幂向有理数指数幂的扩充,而且有理指数幂的运算性质对于无理指数幂也适用,这样指数概念就扩充到了整个实数范围。①分数指数幂的意义及运算性质 ③对于指数幂 ,当指数n扩大至有理数时,要注意底数a的变化范围。如当n=0时底数a≠0;当n为负整数指数时,底数a≠0;当n为分数时,底数a>0。
