3.3 幂函数(18张PPT)
文档属性
| 名称 | 3.3 幂函数(18张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 501.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-04 00:00:00 | ||
图片预览





文档简介
课件18张PPT。幂 函 数1.正分数指数幂,负分数指数幂是如何定义的? 2.求下列函数的定义域:
(1)y = x2 y = x3 y = x ?
(2)y = x-1 y = x-2 y = x -1/2答案:(1)RR[ 0,+∞)(2)(-∞,0)∪(0,+∞)(-∞,0)∪(0,+∞)(0,+∞)复习:幂 函 数一.幂函数的定义:形如 y = xa (a∈R)的函数叫做幂函数,其中 a 是常数.说明: 一般一次函数,二次函数不是幂函数.二.幂函数的定义域:使 x a 有意义的实数的集合.
√Xxx√ 判断下列函数哪些是幂函数,若是判断其奇偶性:
(1)y =5x (2)y =2x (3)y =x0.3
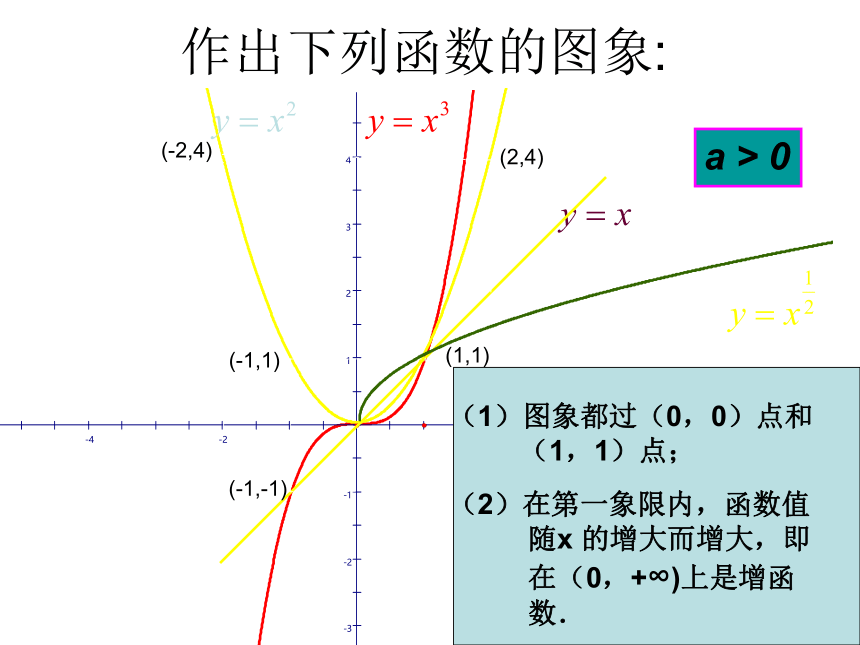
(4)y =x+1 (5)y = (6)y =xxx作出下列函数的图象:(1,1)(2,4)(-2,4)(-1,1)(-1,-1)(1)图象都过(0,0)点和
(1,1)点;
(2)在第一象限内,函数值
随x 的增大而增大,即
在(0,+∞)上是增函
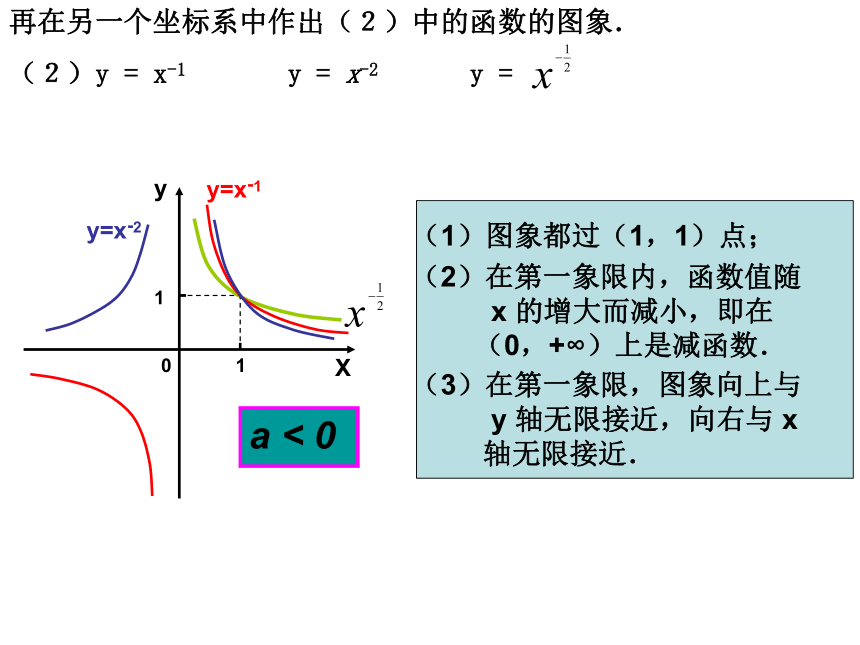
数. a > 0X y110y=x-1y=x-2a < 0 (1)图象都过(1,1)点;
(2)在第一象限内,函数值随
x 的增大而减小,即在
(0,+∞)上是减函数.
(3)在第一象限,图象向上与
y 轴无限接近,向右与 x
轴无限接近.再在另一个坐标系中作出(2)中的函数的图象.
(2)y = x-1 y = x-2 y = <<>>例一、 比较大小:例二、 判断下列幂函数的奇偶性,并在同一坐
标系内画出他们的草图:例三、 解:考虑函数在(-∞,0),(0,+∞)上为单调减函数∴由条件有或或解得: 练习:<><<>>{x|x≠0} 偶函数{x|x≠0} 偶函数{x|x≥0}R 奇函数 ==
(1)y=x0 (2)y=
(3)y= (4)y=x0.2 1.用不等号填空:
(1) (2)
(3) (4)
(5) ____ (6) ___2.求下列幂函数的定义域,并判断其奇偶性:RRR{x|x≠0}{y|y≥0}RR{y|y≠0}{x|x≥0}{y|y≥0}(0,0)(1,1)(0,0)(1,1)(0,0)(1,1)(1,1)(0,0)(1,1)奇函数奇函数奇函数偶函数无Ⅰ,ⅢⅠ,ⅢⅠⅠ,ⅡⅠ,Ⅲ单调增单调增单调增单调增单调减
2.求下列函数的定义域:
(1) (2)课后作业:
1.比较大小:
(1) (2)
(3) (4)
一般幂函数的性质:★所有的幂函数在(0,+∞)都有定义,并且函数图象都通过点(1,1).
★如果α>0,则幂函数的图象过点(0,0),(1,1)并在(0,+∞)上为增函数.
★幂函数的定义域、奇偶性,单调性,
因函数式中α的不同而各异.一般幂函数的性质:★如果α<0,则幂函数的图象过点(1,1),并在(0,+∞)上为减函数.
★当α为奇数时,幂函数为奇函数,
★当α为偶数时,幂函数为偶函数.
例1、(1)已知幂函数y=f(x)的图象过点
,则这个函数的解析式为_______
(2)、已知幂函数 的图象不过原点,求m的值。练习 幂函数 在第一象限的图象如图所示,试比较m、n、p的大小。练习、给定函数解析式:
则图象关于y轴对称的函数是___;
则图象关于原点对称的函数是___;
则互为反函数的两个函数是___。
练习、
1、给定命题:
(1)函数y=x3的图象关于原点成中心对称
(2)函数y=x4的图象关于y轴对称
(3)函数y=x-1的图象关于直线y=x成轴对称
则真命题的个数是____。
2、求函数y=(x-1)-2/3的递增区间___。
3、若函数f(x)=x4/5,g(x)=x-2,则f(g(x))的递增区间___.例3:已知幂函数 f(x)= 为偶函数且在区间 上是单调减函数,
(1)则函数解析式是___;
(2)讨论函数g(x)= 的奇偶性
谢谢大家!
(1)y = x2 y = x3 y = x ?
(2)y = x-1 y = x-2 y = x -1/2答案:(1)RR[ 0,+∞)(2)(-∞,0)∪(0,+∞)(-∞,0)∪(0,+∞)(0,+∞)复习:幂 函 数一.幂函数的定义:形如 y = xa (a∈R)的函数叫做幂函数,其中 a 是常数.说明: 一般一次函数,二次函数不是幂函数.二.幂函数的定义域:使 x a 有意义的实数的集合.
√Xxx√ 判断下列函数哪些是幂函数,若是判断其奇偶性:
(1)y =5x (2)y =2x (3)y =x0.3
(4)y =x+1 (5)y = (6)y =xxx作出下列函数的图象:(1,1)(2,4)(-2,4)(-1,1)(-1,-1)(1)图象都过(0,0)点和
(1,1)点;
(2)在第一象限内,函数值
随x 的增大而增大,即
在(0,+∞)上是增函
数. a > 0X y110y=x-1y=x-2a < 0 (1)图象都过(1,1)点;
(2)在第一象限内,函数值随
x 的增大而减小,即在
(0,+∞)上是减函数.
(3)在第一象限,图象向上与
y 轴无限接近,向右与 x
轴无限接近.再在另一个坐标系中作出(2)中的函数的图象.
(2)y = x-1 y = x-2 y = <<>>例一、 比较大小:例二、 判断下列幂函数的奇偶性,并在同一坐
标系内画出他们的草图:例三、 解:考虑函数在(-∞,0),(0,+∞)上为单调减函数∴由条件有或或解得: 练习:<><<>>{x|x≠0} 偶函数{x|x≠0} 偶函数{x|x≥0}R 奇函数 ==
(1)y=x0 (2)y=
(3)y= (4)y=x0.2 1.用不等号填空:
(1) (2)
(3) (4)
(5) ____ (6) ___2.求下列幂函数的定义域,并判断其奇偶性:RRR{x|x≠0}{y|y≥0}RR{y|y≠0}{x|x≥0}{y|y≥0}(0,0)(1,1)(0,0)(1,1)(0,0)(1,1)(1,1)(0,0)(1,1)奇函数奇函数奇函数偶函数无Ⅰ,ⅢⅠ,ⅢⅠⅠ,ⅡⅠ,Ⅲ单调增单调增单调增单调增单调减
2.求下列函数的定义域:
(1) (2)课后作业:
1.比较大小:
(1) (2)
(3) (4)
一般幂函数的性质:★所有的幂函数在(0,+∞)都有定义,并且函数图象都通过点(1,1).
★如果α>0,则幂函数的图象过点(0,0),(1,1)并在(0,+∞)上为增函数.
★幂函数的定义域、奇偶性,单调性,
因函数式中α的不同而各异.一般幂函数的性质:★如果α<0,则幂函数的图象过点(1,1),并在(0,+∞)上为减函数.
★当α为奇数时,幂函数为奇函数,
★当α为偶数时,幂函数为偶函数.
例1、(1)已知幂函数y=f(x)的图象过点
,则这个函数的解析式为_______
(2)、已知幂函数 的图象不过原点,求m的值。练习 幂函数 在第一象限的图象如图所示,试比较m、n、p的大小。练习、给定函数解析式:
则图象关于y轴对称的函数是___;
则图象关于原点对称的函数是___;
则互为反函数的两个函数是___。
练习、
1、给定命题:
(1)函数y=x3的图象关于原点成中心对称
(2)函数y=x4的图象关于y轴对称
(3)函数y=x-1的图象关于直线y=x成轴对称
则真命题的个数是____。
2、求函数y=(x-1)-2/3的递增区间___。
3、若函数f(x)=x4/5,g(x)=x-2,则f(g(x))的递增区间___.例3:已知幂函数 f(x)= 为偶函数且在区间 上是单调减函数,
(1)则函数解析式是___;
(2)讨论函数g(x)= 的奇偶性
谢谢大家!
