对数的功绩 19张PPT
图片预览






文档简介
课件19张PPT。对数的功绩一光年=299792.458× 31557600
=?km光在真空中的速度 299,792.458 km/s天文学中一年的总秒数31,557,600 s光年:是长度单位,指光在真空中沿直线传播了一年时间的距离。 1543年,哥白尼公布了“日心说”,证明了地球绕着太阳转的事实,1609年伽利略创制了天文望远镜,算出了太阳的自转周期……
天文学的迅速发展使得大规模数学计算的需求变得非常迫切。但是由于当时常量数学的局限性,天文学家不得不花费很大的精力去计算复杂的天文数字。因此浪费了若干年甚至毕生的宝贵时间。16-17世纪,是天文学发展的重要时期.苏格兰数学家
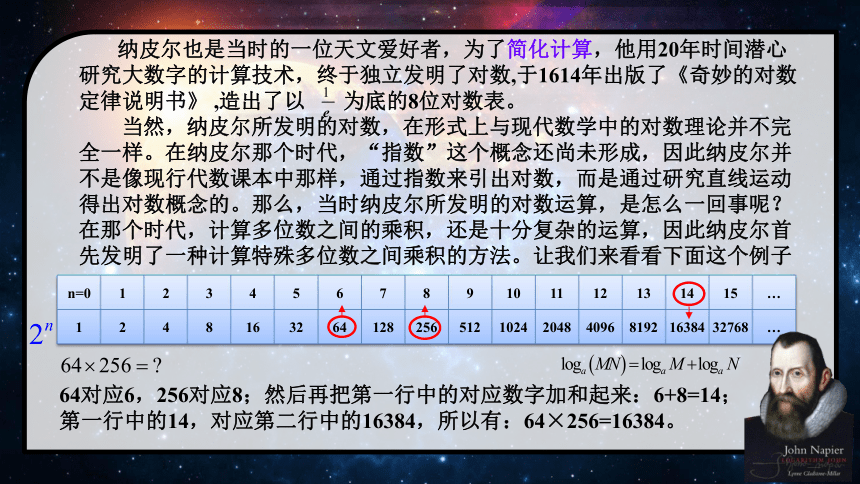
约翰·纳皮尔哥白尼伽利略 纳皮尔也是当时的一位天文爱好者,为了简化计算,他用20年时间潜心研究大数字的计算技术,终于独立发明了对数,于1614年出版了《奇妙的对数定律说明书》 ,造出了以 为底的8位对数表。
当然,纳皮尔所发明的对数,在形式上与现代数学中的对数理论并不完全一样。在纳皮尔那个时代,“指数”这个概念还尚未形成,因此纳皮尔并不是像现行代数课本中那样,通过指数来引出对数,而是通过研究直线运动得出对数概念的。那么,当时纳皮尔所发明的对数运算,是怎么一回事呢?在那个时代,计算多位数之间的乘积,还是十分复杂的运算,因此纳皮尔首先发明了一种计算特殊多位数之间乘积的方法。让我们来看看下面这个例子64对应6,256对应8;然后再把第一行中的对应数字加和起来:6+8=14;第一行中的14,对应第二行中的16384,所以有:64×256=16384。 将对数加以改造使之广泛流传的是纳皮尔的朋友布里格斯,他通过研究《奇妙的对数定律说明书》,感到其中的对数用起来很不方便,于是与纳皮尔商定,使1的对数为0,10的对数为1,这样就得到了以10为底的常用对数,两人共同计算常用对数表。由于所用的数系是十进制,因此它在数值上计算具有优越性。1617年纳皮尔去世,1624年,布里格斯出版了《对数算术》,公布了以10为底包含1~20000及90000~100000的
14位常用对数表。根据对数运算原理,人们还发明了
对数计算尺。300多年来,对数计算尺一直是科学工
作者,特别是工程技术人员必备的计算工具。如果 a > 0,a ? 1,M > 0, N > 0 有: 对数可以把高一级的乘、除、乘方、开方运算分别转化为低一级的加、减、乘、除运算。进行大量的计算时,对数的这种功能,可使效率成倍地提高。简化计算 299792.458× 31557600 =x= 299792.458× 31557600lgx=lg299792.458+lg31553600x ≈ 9.46×1012 km查表=5.477+5.499+2=10.976反查对数表一光年等于九万四千六百亿千米。一光年的距离相当于地球和月球距离的2500万倍,太阳和地球距离的6.3万倍。一光年的距离可以并排放下7.4亿个地球,680万个太阳。天体距离计算细菌半径计算例1 在我们体内,繁殖着一些让我们生病的细菌。某种球菌的体积求这种细菌的半径r?两边同时取常用对数,得细菌计算 由于对数的发展早于指数,人们对对数的认识,只停留在简化计算上,对其他性质并不了解。
直到瑞士大数学家欧拉,理顺了指数与对数的关系,
提出“对数源于指数”之后,对数才被世人广泛接受。
随着计算工具的不断变革与普及,对数表逐渐淡出了人们的视野,我们若要算x=lg964的近似值,只需在计算器上按顺序按键 即可。
但这段横跨200多年,跌宕起伏,动人心魄的发展史仍耐人寻味。
如今,对数仍然在很多领域发光发热!
你知道下面两个数字的差异吗? 0.0000000398 会导致有人游泳后眼睛变红吗?比较大小0.00000000398为溶液中氢离子的物质量浓度0.00000003980.000000003988.47.4氢离子浓度指数,一般称为“pH”,是1909年由丹麦生物化学家?斯温·彼得·索伦森提出。比较大小电影《末日崩塌》
9.6级超级地震2019年5月18日
吉林松原
5.1级地震 地震的级数就是当地震发生时,以地震波的形式放出的能量的指示参数
其中M为里克特级数,是由美国地震学家里克特和古登堡于1935年所制定,它直接同震源中心释放的能量(热能和动能)大小有关,震源放出的能量越大,震级就越大。
M=lgA-lgA0 (A振幅,A0表示地震强度为1微米的地震)地震能量E与里克特级数M关系式:lgE=4.8+1.5M为什么对数可以把大数变小方便比较
还能把小数变大呢? 下表数据为航空发动机
叶片的工作温度与对应寿命 请用excel作出发动机叶片温度-寿命曲线,并估计出叶片工作温度为1700K时的寿命?(K为热力学温度单位,开尔文开氏温度)
下表数据为航空发动机
叶片的工作温度与对应寿命20,0004.34.4830,0003,000,000 请用excel作出发动机叶片温度-寿命曲线,并估计出叶片工作温度为1700K时的寿命?(K为热力学温度单位,开尔文开氏温度)
伟大的导师恩格斯在他的著作《自然辩证法》中,曾经把笛卡尔的坐标、纳皮尔的对数、牛顿和莱布尼兹的微积分共同称为十七世纪的三大数学发明。
法国著名的数学家、天文学家拉普拉斯(Pierre Simon Laplace,1749-1827)曾说对数可以缩短计算时间,“在实效上等于把天文学家的寿命延长了许多倍。
伽利略甚至说:“给我空间、时间及对数,
我即可创造一个宇宙。”
=?km光在真空中的速度 299,792.458 km/s天文学中一年的总秒数31,557,600 s光年:是长度单位,指光在真空中沿直线传播了一年时间的距离。 1543年,哥白尼公布了“日心说”,证明了地球绕着太阳转的事实,1609年伽利略创制了天文望远镜,算出了太阳的自转周期……
天文学的迅速发展使得大规模数学计算的需求变得非常迫切。但是由于当时常量数学的局限性,天文学家不得不花费很大的精力去计算复杂的天文数字。因此浪费了若干年甚至毕生的宝贵时间。16-17世纪,是天文学发展的重要时期.苏格兰数学家
约翰·纳皮尔哥白尼伽利略 纳皮尔也是当时的一位天文爱好者,为了简化计算,他用20年时间潜心研究大数字的计算技术,终于独立发明了对数,于1614年出版了《奇妙的对数定律说明书》 ,造出了以 为底的8位对数表。
当然,纳皮尔所发明的对数,在形式上与现代数学中的对数理论并不完全一样。在纳皮尔那个时代,“指数”这个概念还尚未形成,因此纳皮尔并不是像现行代数课本中那样,通过指数来引出对数,而是通过研究直线运动得出对数概念的。那么,当时纳皮尔所发明的对数运算,是怎么一回事呢?在那个时代,计算多位数之间的乘积,还是十分复杂的运算,因此纳皮尔首先发明了一种计算特殊多位数之间乘积的方法。让我们来看看下面这个例子64对应6,256对应8;然后再把第一行中的对应数字加和起来:6+8=14;第一行中的14,对应第二行中的16384,所以有:64×256=16384。 将对数加以改造使之广泛流传的是纳皮尔的朋友布里格斯,他通过研究《奇妙的对数定律说明书》,感到其中的对数用起来很不方便,于是与纳皮尔商定,使1的对数为0,10的对数为1,这样就得到了以10为底的常用对数,两人共同计算常用对数表。由于所用的数系是十进制,因此它在数值上计算具有优越性。1617年纳皮尔去世,1624年,布里格斯出版了《对数算术》,公布了以10为底包含1~20000及90000~100000的
14位常用对数表。根据对数运算原理,人们还发明了
对数计算尺。300多年来,对数计算尺一直是科学工
作者,特别是工程技术人员必备的计算工具。如果 a > 0,a ? 1,M > 0, N > 0 有: 对数可以把高一级的乘、除、乘方、开方运算分别转化为低一级的加、减、乘、除运算。进行大量的计算时,对数的这种功能,可使效率成倍地提高。简化计算 299792.458× 31557600 =x= 299792.458× 31557600lgx=lg299792.458+lg31553600x ≈ 9.46×1012 km查表=5.477+5.499+2=10.976反查对数表一光年等于九万四千六百亿千米。一光年的距离相当于地球和月球距离的2500万倍,太阳和地球距离的6.3万倍。一光年的距离可以并排放下7.4亿个地球,680万个太阳。天体距离计算细菌半径计算例1 在我们体内,繁殖着一些让我们生病的细菌。某种球菌的体积求这种细菌的半径r?两边同时取常用对数,得细菌计算 由于对数的发展早于指数,人们对对数的认识,只停留在简化计算上,对其他性质并不了解。
直到瑞士大数学家欧拉,理顺了指数与对数的关系,
提出“对数源于指数”之后,对数才被世人广泛接受。
随着计算工具的不断变革与普及,对数表逐渐淡出了人们的视野,我们若要算x=lg964的近似值,只需在计算器上按顺序按键 即可。
但这段横跨200多年,跌宕起伏,动人心魄的发展史仍耐人寻味。
如今,对数仍然在很多领域发光发热!
你知道下面两个数字的差异吗? 0.0000000398 会导致有人游泳后眼睛变红吗?比较大小0.00000000398为溶液中氢离子的物质量浓度0.00000003980.000000003988.47.4氢离子浓度指数,一般称为“pH”,是1909年由丹麦生物化学家?斯温·彼得·索伦森提出。比较大小电影《末日崩塌》
9.6级超级地震2019年5月18日
吉林松原
5.1级地震 地震的级数就是当地震发生时,以地震波的形式放出的能量的指示参数
其中M为里克特级数,是由美国地震学家里克特和古登堡于1935年所制定,它直接同震源中心释放的能量(热能和动能)大小有关,震源放出的能量越大,震级就越大。
M=lgA-lgA0 (A振幅,A0表示地震强度为1微米的地震)地震能量E与里克特级数M关系式:lgE=4.8+1.5M为什么对数可以把大数变小方便比较
还能把小数变大呢? 下表数据为航空发动机
叶片的工作温度与对应寿命 请用excel作出发动机叶片温度-寿命曲线,并估计出叶片工作温度为1700K时的寿命?(K为热力学温度单位,开尔文开氏温度)
下表数据为航空发动机
叶片的工作温度与对应寿命20,0004.34.4830,0003,000,000 请用excel作出发动机叶片温度-寿命曲线,并估计出叶片工作温度为1700K时的寿命?(K为热力学温度单位,开尔文开氏温度)
伟大的导师恩格斯在他的著作《自然辩证法》中,曾经把笛卡尔的坐标、纳皮尔的对数、牛顿和莱布尼兹的微积分共同称为十七世纪的三大数学发明。
法国著名的数学家、天文学家拉普拉斯(Pierre Simon Laplace,1749-1827)曾说对数可以缩短计算时间,“在实效上等于把天文学家的寿命延长了许多倍。
伽利略甚至说:“给我空间、时间及对数,
我即可创造一个宇宙。”
