1.1.1 不等式的基本性质 课件25张PPT
文档属性
| 名称 | 1.1.1 不等式的基本性质 课件25张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 705.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-04 11:15:18 | ||
图片预览






文档简介
课件25张PPT。选修4-5 1.1.1不等式的基本性质高矮大小多少短长轻重不等式的基本性质选修4-5 1.1.11.实数在数轴上的性质:数轴上
的点一一对应p3基本理论研究不等式的出发点是实数的大小关系。数轴上的点与实数一一对应,因此可以利用
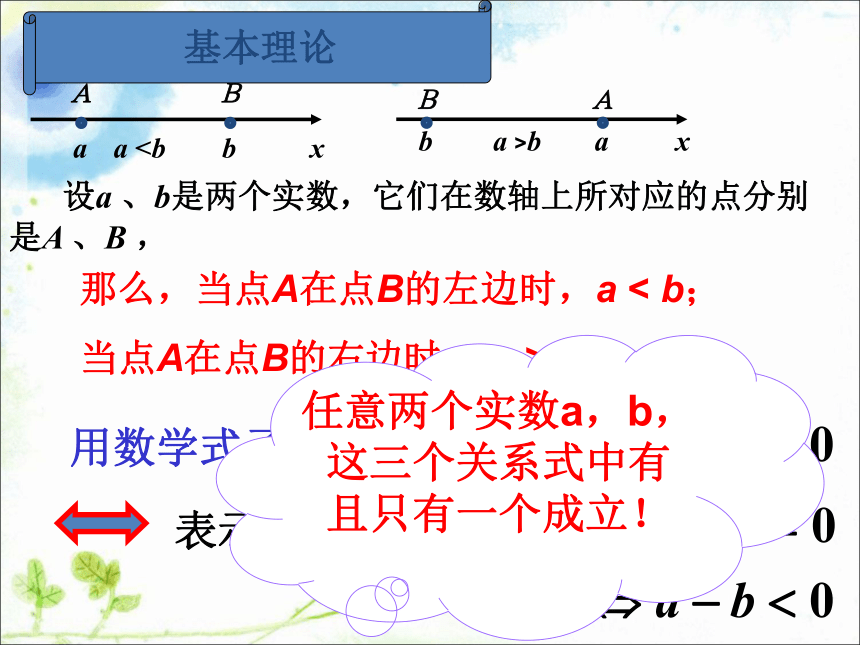
数轴上点的左右位置关系来规定实数的大小:ABababx用数学式子表示为: 设a 、b是两个实数,它们在数轴上所对应的点分别是A 、B ,基本理论那么,当点A在点B的左边时,a < b;
当点A在点B的右边时, a > b.表示“等价于”任意两个实数a,b,这三个关系式中有且只有一个成立! 要比较两个实数a与b的大小,可以转化为比较它们的差与0的大小.
在这里,0为实数比较大小提供了“标杆”.思考:从上述事实出发,你认为可以用什么方法比较两个实数的大小?思想方法<<作差定号下结论变形自主学习例 1
注:常见的变形手段是: 通分、因式分解或配方等;变形的结果是常数、若干个因式的积或完全平方式等. 练习1比较
的大小。
应用(1)证明函数的单调性
(2)f(x)> g(x)恒成立,则需构造函数F(x)= f(x)- g(x)证明F(x)的最小值大于0.合作提高课后思考:如果作差的结果为不能定号的代数式,又该怎么讨论? 等式有“等式两边加或减同一个数,等式仍然成立”, “等式两边乘或除以同一个数,等式仍然成立”等性质,类比等式的基本性质,不等式有哪些基本性质呢?联系实数的运算(加,减,乘,除,乘方,开方等)来思考不等式的基本性质研究实数的关系时联系实数的运算,是一种基本的数学思想探究由两个实数大小关系的基本事实,得出不等式的基本性质:对称性传递性加法法则乘法法则乘方法则开方法则基本性质课后思考:性质(5)在必修5第三章中限制条件不同,对n的限制可以改为n 〉0吗?思考:你能写出当a2.上述基本事实和基本性质是我们处理不等式问题的基本依据,以它们作为研究的出发点。(同向不等式相加)例如,利用不等式的基本性质可以得到下列结论:(同向正数不等式相乘)(移项法则)(同号两数,大的倒数较小,小的倒数较大。)(ⅲ)(ⅳ)不可相减不可相除(ⅳ)证明:性质4可利用y=1/x图像和性质证明
①②由①②可得性质4性质4性质2性质6实数的大小作差比较还有其他方法吗?回忆推论4的证明推论3性质6性质41.分析证明思路(已知,求证)例题小结:
2.应用基本事实和基本性质
(注意使用的条件)3.规范地写出证明过程,注意推理 的严谨性。练习2:证明:性质4推论2推论4性质1推论31.任务验收:在回顾和复习不等式的过程中,对不等式的基本性质进行系统地归纳整理,加深理解和应用。课堂小结
2.思想方法:数形结合、联系实数运算、与等式性质作类比多角度辨析、理解3.对不等式性质和推论的理解应用
使用不等式的性质和推论时,一定要清楚它们成立的前提条件,不可强化或弱化它们成立的条件,盲目套用。课堂小结2.比较两个实数大小的主要方法:(1)作差比较法:作差——变形——定号——下结论;课堂小结与作业3.不等式的基本性质. (6条)课外作业:
1.识记不等式的基本性质
2.P9 第一题(真命题加以证明)
第二题(写在本上)
3.完成课堂上提出的思考1.不等关系:
的点一一对应p3基本理论研究不等式的出发点是实数的大小关系。数轴上的点与实数一一对应,因此可以利用
数轴上点的左右位置关系来规定实数的大小:ABaba
当点A在点B的右边时, a > b.表示“等价于”任意两个实数a,b,这三个关系式中有且只有一个成立! 要比较两个实数a与b的大小,可以转化为比较它们的差与0的大小.
在这里,0为实数比较大小提供了“标杆”.思考:从上述事实出发,你认为可以用什么方法比较两个实数的大小?思想方法<<作差定号下结论变形自主学习例 1
注:常见的变形手段是: 通分、因式分解或配方等;变形的结果是常数、若干个因式的积或完全平方式等. 练习1比较
的大小。
应用(1)证明函数的单调性
(2)f(x)> g(x)恒成立,则需构造函数F(x)= f(x)- g(x)证明F(x)的最小值大于0.合作提高课后思考:如果作差的结果为不能定号的代数式,又该怎么讨论? 等式有“等式两边加或减同一个数,等式仍然成立”, “等式两边乘或除以同一个数,等式仍然成立”等性质,类比等式的基本性质,不等式有哪些基本性质呢?联系实数的运算(加,减,乘,除,乘方,开方等)来思考不等式的基本性质研究实数的关系时联系实数的运算,是一种基本的数学思想探究由两个实数大小关系的基本事实,得出不等式的基本性质:对称性传递性加法法则乘法法则乘方法则开方法则基本性质课后思考:性质(5)在必修5第三章中限制条件不同,对n的限制可以改为n 〉0吗?思考:你能写出当a
①②由①②可得性质4性质4性质2性质6实数的大小作差比较还有其他方法吗?回忆推论4的证明推论3性质6性质41.分析证明思路(已知,求证)例题小结:
2.应用基本事实和基本性质
(注意使用的条件)3.规范地写出证明过程,注意推理 的严谨性。练习2:证明:性质4推论2推论4性质1推论31.任务验收:在回顾和复习不等式的过程中,对不等式的基本性质进行系统地归纳整理,加深理解和应用。课堂小结
2.思想方法:数形结合、联系实数运算、与等式性质作类比多角度辨析、理解3.对不等式性质和推论的理解应用
使用不等式的性质和推论时,一定要清楚它们成立的前提条件,不可强化或弱化它们成立的条件,盲目套用。课堂小结2.比较两个实数大小的主要方法:(1)作差比较法:作差——变形——定号——下结论;课堂小结与作业3.不等式的基本性质. (6条)课外作业:
1.识记不等式的基本性质
2.P9 第一题(真命题加以证明)
第二题(写在本上)
3.完成课堂上提出的思考1.不等关系:
