1.5.3 反证法和放缩法 课件 37张PPT
文档属性
| 名称 | 1.5.3 反证法和放缩法 课件 37张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 485.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-03 23:08:05 | ||
图片预览




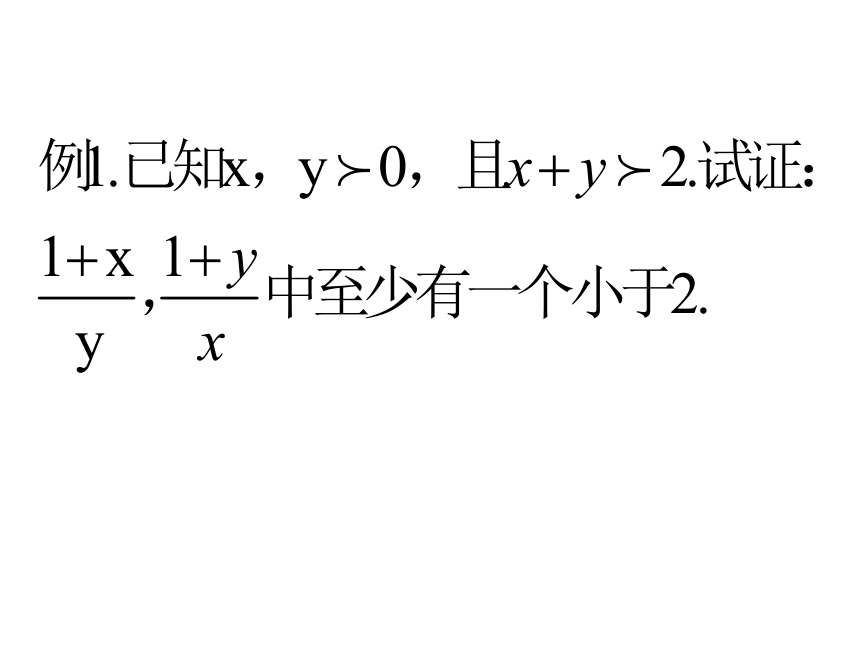







文档简介
课件37张PPT。反证法 先假设要证明的命题不成立,以此为出发点,结合已知条件,应用公理、定义、定理、性质等,进行正确的推理,得到矛盾,说明假设不正确,从而间接说明原命题成立的方法。
常见的涉及反证法的文字语言及其相对应的否定假设.
对某些数学语言的否定假设要准确,以免造成原则性的错误,有时在使用反证法时,对假设的否定也可以举一定的特例来说明矛盾,尤其在一些选择题中,更是如此.用反证法证明不等式应注意的问题:
(1)必须先否定结论,对于结论的反面出现的多种可能要逐一论证,缺少任何一种可能,证明都是不完全的.(2)反证法必须从否定结论进行推理,且必须根据
这一条件进行论证;否则,仅否定结论,不从结论
的反面出发进行论证,就不是反证法.
(3)推导出来的矛盾可以是多种多样的,有的与已知条件相矛盾,有的与假设相矛盾,有的与定理、公理相违背,有的与已知的事实相矛盾等,总之推导出的矛盾必须是明显的.例2、已知a + b + c > 0,ab + bc + ca > 0,
abc > 0, 求证:a, b, c > 0
证:设a < 0, ∵abc > 0, ∴bc < 0
又由a + b + c > 0, 则b + c > ?a > 0
∴ab + bc + ca = a(b + c) + bc < 0
与题设矛盾
若a = 0,则与abc > 0矛盾,
∴必有a > 0
同理可证:b > 0, c > 0例3、设0 < a, b, c < 1,求证:(1 ? a)b, (1 ? b)c, (1 ? c)a,
不可能同时大于1/4则三式相乘: (1 ? a)b?(1 ? b)c?(1 ? c)a > 又∵0 < a, b, c < 1 ∴同理:以上三式相乘: (1 ? a)a?(1 ? b)b?(1 ? c)c≤与①矛盾∴结论成立证明:设(1 ? a)b>1/4, (1 ? b)c>1/4, (1 ?c)a>1/4,【例】△ABC的三边长a,b,c的倒数成等差数列,求证:∠B<90°.
【分析】本题中的条件是三边间的关系 ,而要证明的是∠B与90°的大小关系.结论与条件之间的关系不明显,考虑用反证法证明.【解答】∵a、b、c的倒数成等差数列, 假设∠B<90°不成立,即∠B≥90°,则∠B是三角形的最大内角,在三角形中,有大角对大边,∴b>a>0,b>c>0.
这与 相矛盾.
∴假设不成立,故∠B<90°成立.【拓展】若a3+b3=2,求证:a+b≤2.
【分析】本题结论的反面比原结论更具体,
更简洁,宜用反证法.【证明】假设a+b>2,则(a+b)3=a3+b3+3ab(a+b)>8.
由a3+b3=2,得3ab(a+b)>6.
故ab(a+b)>2.
又a3+b3=(a+b)(a2-ab+b2)=2,
∴ab(a+b)>(a+b)(a2-ab+b2),
∴a2-ab+b2<ab,
即(a-b)2<0.这不可能,故a+b≤2.用反证法证“至多”、“至少”型问题的方法与步骤.
(1)反证法的一般步骤:
①否定结论:假设要证明的结论不成立,即假设结论的反面成立.
②推理论证:由“否定结论”出发,通过正确的推理,导出矛盾.
③肯定结论:因为推理正确,产生矛盾的原因在于“否定”结论的错误,即结论的反面不成立,从而结论成立.用反证法证“至多”、“至少”型问题(2)在证明中含有“至多”、“至少”、“最多”等字眼时,若正面难以找到解题的突破口,可转换视角,用反证法证明.在用反证法证明的过程中,由于作出了与结论相反的假设,相当于增加了题设条件,因此在证明过程中必须使用这个增加的条件,否则将无法推出矛盾.练习:否定“自然数a、b、c中恰有一个为偶数”时正确的反设为( )
(A)a、b、c都是奇数
(B)a、b、c都是偶数
(C)a、b、c中至少有两个偶数
(D)a、b、c中至少有两个偶数或都是奇数
【解析】选D.三个自然数的奇偶情况有“三偶、三奇、二偶一奇、二奇一偶”4种,而自然数a、b、c中恰有一个为偶数包含“二奇一偶”的情况,故反面的情况有3种,只有D项符合.练习:设a,b是两个实数,给出下列条件:
(1)a+b>1;(2)a+b=2;(3)a+b>2;(4)a2+b2>2;(5)ab>1,其中能推出“a,b中至少有一个大于1”的条件是( )
(A)(2)(3) (B)(1)(2)
(C)(3) (D)(4)(5)
【解析】选C.(1)可取a=0.5,b=0.6,故不正确;(2)若a+b=2,则可取a=1,b=1;(3)若a+b>2,则a,b中至少有一个大于1,正确;(4)若a2+b2>2,可取a=-2,b=-1;(5)若ab>1,则可取a=-2,b=-1,故选C.例:实数a、b、c、d满足a+b=c+d=1,ac+bd>1.
求证:a、b、c、d中至少有一个是负数.
【证明】
假设a、b、c、d都是非负数.
即a≥0,b≥0,c≥0,d≥0
则1=(a+b)(c+d)=(ac+bd)+(ad+bc)≥ac+bd.
这与已知中ac+bd>1矛盾,∴原假设错误,
故a、b、c、d中至少有一个是负数.【例】(2011·南通模拟)若a、b、c均为实数,且
求证:a、b、c中至少有一个大于0.
【分析】本题是一个“至少”成立的问题且a、b、c是含有x、y、z的代数式,从正面证明难度较大,可考虑反证法.【解答】假设a、b、c都不大于0,即a≤0,b≤0,c≤0,∴a+b+c≤0.
而
=(x2-2x)+(y2-2y)+(z2-2z)+π
=(x-1)2+(y-1)2+(z-1)2+π-3
∴a+b+c>0.这与a+b+c≤0矛盾,
故a、b、c中至少有一个大于0.【拓展】已知f(x)=x2+bx+c,求证:
|f(1)|、|f(2)|、|f(3)|中至少有一个不小于 .
【分析】(1)本题是一个“至少”成立的问题,用反证法证明较简单.
(2)“不小于”的否定是“小于”,问题转化为三个绝对值的式子小于 同时成立,解绝对值不等式组,判断是否能推出一个矛盾结论.【证明】方法一:假设 则
与②矛盾.∴假设不成立,
∴|f(1)|、|f(2)|、|f(3)|中至少有一个不小于 放缩法放缩法证明不等式的技巧:
放缩法是不等式证明的基本方法,在不等式证明中几乎处处存在.
(1)放缩法证明不等式时,常见的放缩依据或技巧主要有:①不等式的传递性;
②同分子(母)异分母(子)的两个分式大小的比较.缩小分母、扩大分子,分式值增大;缩小分子、扩大分母,分式值减小;(2)放缩法的注意事项
①舍去或加上一些项,如:
②将分子或分母放大(缩小),如:
特别注意:放大或缩小时注意要适当,必须目标明确,合情合理,恰到好处,且不可放缩过大或过小。例1、若a, b, c, d?R+,求证:证:记m = ∵a, b, c, d?R+ ∴1 < m < 2 即原式成立 法1: 证明:在 时,显然成立.当 时,左边 法2:法3:函数的方法【例】设
求证:
【证明】练习书29页2题【练习】已知a>0,b>0,c>0,a+b>c.
求证:
【分析】本题若通分去分母,运算量较大,考虑到a>0,b>0可先试试分式的放缩.【证明】∵a>0,b>0,
∴只需证:
而函数 在(0,+∞)上递增,
且a+b>c,∴f(a+b)>f(c).
即
∴原不等式成立.练习:设x>0,y>0,若 则A、B的大小关系为_______.
【解析】∵x>0,y>0,
答案:A<B【例】已知数列{an}的通项公式为
若
求证:2n【分析】(1)求出通项bn才能尝试证明不等式;
(2)代入an的有关表达式后,用n表示bn,再用基本不等式进行放缩.【解答】【练习】已知实数x、y、z不全为零,求证:
【分析】不等式左边都是根式,右边是整式,可考虑将根号内的式子配方后,再用放缩法证明.【解答】
同理可证:
由于x,y,z不全为零,故上述三式中至少有一式取不到等号,所以三式累加得:
练习:在△ABC中,∠A、∠B、∠C所对的边分别为a、b、c且a、b、c成等差数列,则∠B适合的条件是( )
(A)0<∠B≤ (B)0<∠B≤
(C)0<∠B≤ (D) <∠B<π
【解析】选B.因为2b=a+c,所以练习:设 则( )
(A)M=1 (B)M>1 (C)M<1 (D)M≥1
【解析】选C.
常见的涉及反证法的文字语言及其相对应的否定假设.
对某些数学语言的否定假设要准确,以免造成原则性的错误,有时在使用反证法时,对假设的否定也可以举一定的特例来说明矛盾,尤其在一些选择题中,更是如此.用反证法证明不等式应注意的问题:
(1)必须先否定结论,对于结论的反面出现的多种可能要逐一论证,缺少任何一种可能,证明都是不完全的.(2)反证法必须从否定结论进行推理,且必须根据
这一条件进行论证;否则,仅否定结论,不从结论
的反面出发进行论证,就不是反证法.
(3)推导出来的矛盾可以是多种多样的,有的与已知条件相矛盾,有的与假设相矛盾,有的与定理、公理相违背,有的与已知的事实相矛盾等,总之推导出的矛盾必须是明显的.例2、已知a + b + c > 0,ab + bc + ca > 0,
abc > 0, 求证:a, b, c > 0
证:设a < 0, ∵abc > 0, ∴bc < 0
又由a + b + c > 0, 则b + c > ?a > 0
∴ab + bc + ca = a(b + c) + bc < 0
与题设矛盾
若a = 0,则与abc > 0矛盾,
∴必有a > 0
同理可证:b > 0, c > 0例3、设0 < a, b, c < 1,求证:(1 ? a)b, (1 ? b)c, (1 ? c)a,
不可能同时大于1/4则三式相乘: (1 ? a)b?(1 ? b)c?(1 ? c)a > 又∵0 < a, b, c < 1 ∴同理:以上三式相乘: (1 ? a)a?(1 ? b)b?(1 ? c)c≤与①矛盾∴结论成立证明:设(1 ? a)b>1/4, (1 ? b)c>1/4, (1 ?c)a>1/4,【例】△ABC的三边长a,b,c的倒数成等差数列,求证:∠B<90°.
【分析】本题中的条件是三边间的关系 ,而要证明的是∠B与90°的大小关系.结论与条件之间的关系不明显,考虑用反证法证明.【解答】∵a、b、c的倒数成等差数列, 假设∠B<90°不成立,即∠B≥90°,则∠B是三角形的最大内角,在三角形中,有大角对大边,∴b>a>0,b>c>0.
这与 相矛盾.
∴假设不成立,故∠B<90°成立.【拓展】若a3+b3=2,求证:a+b≤2.
【分析】本题结论的反面比原结论更具体,
更简洁,宜用反证法.【证明】假设a+b>2,则(a+b)3=a3+b3+3ab(a+b)>8.
由a3+b3=2,得3ab(a+b)>6.
故ab(a+b)>2.
又a3+b3=(a+b)(a2-ab+b2)=2,
∴ab(a+b)>(a+b)(a2-ab+b2),
∴a2-ab+b2<ab,
即(a-b)2<0.这不可能,故a+b≤2.用反证法证“至多”、“至少”型问题的方法与步骤.
(1)反证法的一般步骤:
①否定结论:假设要证明的结论不成立,即假设结论的反面成立.
②推理论证:由“否定结论”出发,通过正确的推理,导出矛盾.
③肯定结论:因为推理正确,产生矛盾的原因在于“否定”结论的错误,即结论的反面不成立,从而结论成立.用反证法证“至多”、“至少”型问题(2)在证明中含有“至多”、“至少”、“最多”等字眼时,若正面难以找到解题的突破口,可转换视角,用反证法证明.在用反证法证明的过程中,由于作出了与结论相反的假设,相当于增加了题设条件,因此在证明过程中必须使用这个增加的条件,否则将无法推出矛盾.练习:否定“自然数a、b、c中恰有一个为偶数”时正确的反设为( )
(A)a、b、c都是奇数
(B)a、b、c都是偶数
(C)a、b、c中至少有两个偶数
(D)a、b、c中至少有两个偶数或都是奇数
【解析】选D.三个自然数的奇偶情况有“三偶、三奇、二偶一奇、二奇一偶”4种,而自然数a、b、c中恰有一个为偶数包含“二奇一偶”的情况,故反面的情况有3种,只有D项符合.练习:设a,b是两个实数,给出下列条件:
(1)a+b>1;(2)a+b=2;(3)a+b>2;(4)a2+b2>2;(5)ab>1,其中能推出“a,b中至少有一个大于1”的条件是( )
(A)(2)(3) (B)(1)(2)
(C)(3) (D)(4)(5)
【解析】选C.(1)可取a=0.5,b=0.6,故不正确;(2)若a+b=2,则可取a=1,b=1;(3)若a+b>2,则a,b中至少有一个大于1,正确;(4)若a2+b2>2,可取a=-2,b=-1;(5)若ab>1,则可取a=-2,b=-1,故选C.例:实数a、b、c、d满足a+b=c+d=1,ac+bd>1.
求证:a、b、c、d中至少有一个是负数.
【证明】
假设a、b、c、d都是非负数.
即a≥0,b≥0,c≥0,d≥0
则1=(a+b)(c+d)=(ac+bd)+(ad+bc)≥ac+bd.
这与已知中ac+bd>1矛盾,∴原假设错误,
故a、b、c、d中至少有一个是负数.【例】(2011·南通模拟)若a、b、c均为实数,且
求证:a、b、c中至少有一个大于0.
【分析】本题是一个“至少”成立的问题且a、b、c是含有x、y、z的代数式,从正面证明难度较大,可考虑反证法.【解答】假设a、b、c都不大于0,即a≤0,b≤0,c≤0,∴a+b+c≤0.
而
=(x2-2x)+(y2-2y)+(z2-2z)+π
=(x-1)2+(y-1)2+(z-1)2+π-3
∴a+b+c>0.这与a+b+c≤0矛盾,
故a、b、c中至少有一个大于0.【拓展】已知f(x)=x2+bx+c,求证:
|f(1)|、|f(2)|、|f(3)|中至少有一个不小于 .
【分析】(1)本题是一个“至少”成立的问题,用反证法证明较简单.
(2)“不小于”的否定是“小于”,问题转化为三个绝对值的式子小于 同时成立,解绝对值不等式组,判断是否能推出一个矛盾结论.【证明】方法一:假设 则
与②矛盾.∴假设不成立,
∴|f(1)|、|f(2)|、|f(3)|中至少有一个不小于 放缩法放缩法证明不等式的技巧:
放缩法是不等式证明的基本方法,在不等式证明中几乎处处存在.
(1)放缩法证明不等式时,常见的放缩依据或技巧主要有:①不等式的传递性;
②同分子(母)异分母(子)的两个分式大小的比较.缩小分母、扩大分子,分式值增大;缩小分子、扩大分母,分式值减小;(2)放缩法的注意事项
①舍去或加上一些项,如:
②将分子或分母放大(缩小),如:
特别注意:放大或缩小时注意要适当,必须目标明确,合情合理,恰到好处,且不可放缩过大或过小。例1、若a, b, c, d?R+,求证:证:记m = ∵a, b, c, d?R+ ∴1 < m < 2 即原式成立 法1: 证明:在 时,显然成立.当 时,左边 法2:法3:函数的方法【例】设
求证:
【证明】练习书29页2题【练习】已知a>0,b>0,c>0,a+b>c.
求证:
【分析】本题若通分去分母,运算量较大,考虑到a>0,b>0可先试试分式的放缩.【证明】∵a>0,b>0,
∴只需证:
而函数 在(0,+∞)上递增,
且a+b>c,∴f(a+b)>f(c).
即
∴原不等式成立.练习:设x>0,y>0,若 则A、B的大小关系为_______.
【解析】∵x>0,y>0,
答案:A<B【例】已知数列{an}的通项公式为
若
求证:2n
(2)代入an的有关表达式后,用n表示bn,再用基本不等式进行放缩.【解答】【练习】已知实数x、y、z不全为零,求证:
【分析】不等式左边都是根式,右边是整式,可考虑将根号内的式子配方后,再用放缩法证明.【解答】
同理可证:
由于x,y,z不全为零,故上述三式中至少有一式取不到等号,所以三式累加得:
练习:在△ABC中,∠A、∠B、∠C所对的边分别为a、b、c且a、b、c成等差数列,则∠B适合的条件是( )
(A)0<∠B≤ (B)0<∠B≤
(C)0<∠B≤ (D) <∠B<π
【解析】选B.因为2b=a+c,所以练习:设 则( )
(A)M=1 (B)M>1 (C)M<1 (D)M≥1
【解析】选C.
