1.5.3 反证法和放缩法 课件 18张PPT
文档属性
| 名称 | 1.5.3 反证法和放缩法 课件 18张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 709.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-04 00:00:00 | ||
图片预览





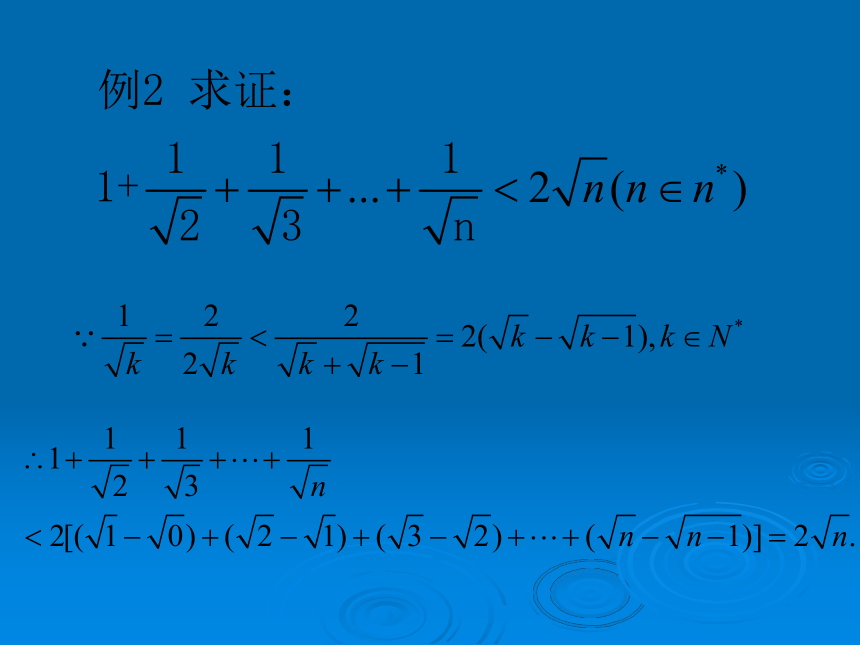
文档简介
课件18张PPT。不等式的证明知识点回顾不等式证明的常用方法:
1.比较法、
综合法、分析法
构造函数法
反证法
【典型例题】例1、若a, b, c, d?R+,求证:证:记m = ∵a, b, c, d?R+ ∴1 < m < 2 即原式成立例1小结(1)所谓放缩法就是利用不等式的传递性,对照证题目标进行合情合理的放大和缩小的过程。
(2)所谓放缩的技巧:即对欲证 ,寻找一个(或多个)中间变量C,使 ,由A到C叫做“放”,由B到C叫做“缩”。
(3)使用放缩法证题时要注意放和缩的“度”,否则就不能同向传递了。
(4)分式放缩:一个分式若分子变大则分式值变大,若分母变大则分式值变小,一个真分式,分子、分母同时加上同一个正数则分式值变大,利用这些性质,可达到证题目的。
变式练习11.已知a、b、c为三角形的三边,
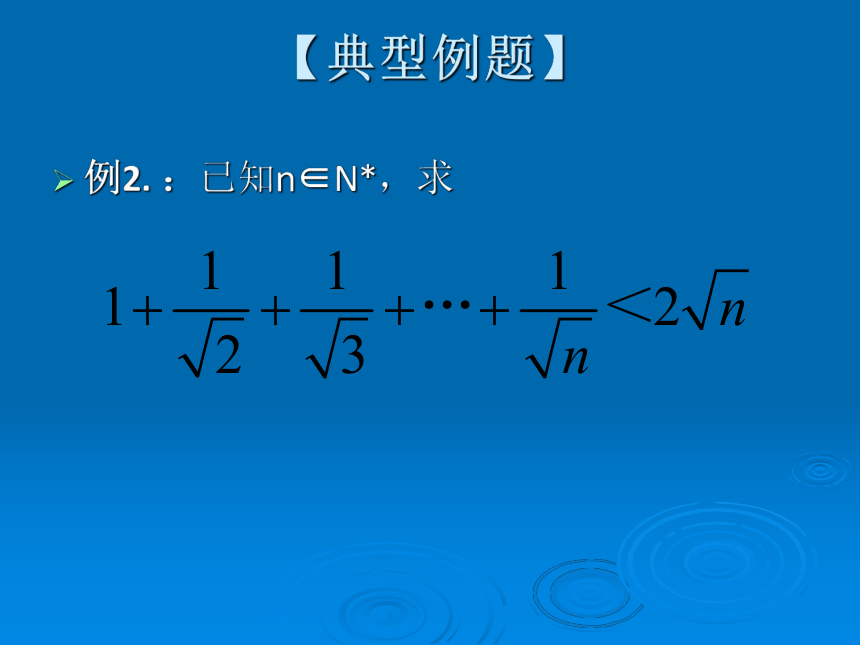
求证: 【典型例题】 例2. :已知n∈N*,求 例2小结若欲证不等式含有与自然数n有关的n项和,可采用数列中裂项求和等方法来解题。
方法:裂项放缩
变式练习2【变式】例3、巳知:a、b、c∈ ,求证:略解【典型例题】例3小结
“添舍”放缩:
通过对不等式的一边进行添项或减项以达到解题目的,这是常规思路。
变式练习3 已知a,b,c不全为零,求证:【典型例题】 例4 : 求证:lg3 ·lg33<1 例4小结方法:公式放缩
利用已知的公式或恒不等式,把欲证不等式变形后再放缩,可获简解。
变式练习4 1、当 n > 2 时,求证: 证:∵n > 2 ∴ ∴n > 2时, 课堂小结1、用“放缩法”证明不等式的关键在于根据问题的特征选择恰当的方法,有时还需要几种方法融为一体。
2、在证明过程中,适当地进行放缩,可以化繁为简、化难为易,达到事半功倍的效果。但放缩的范围较难把握,常常出现放缩后得不出结论或得到相反的现象。因此,使用放缩法时,如何确定放缩目标尤为重要。要想正确确定放缩目标,就必须根据欲证结论,抓住题目的特点。
课堂小结3、掌握放缩技巧,真正做到弄懂弄通,并且还要根据不同题目的类型,采用恰到好处的放缩方法,才能把题解活,从而培养和提高自己的思维和逻辑推理能力,分析问题和解决问题的能力。谢谢啦
1.比较法、
综合法、分析法
构造函数法
反证法
【典型例题】例1、若a, b, c, d?R+,求证:证:记m = ∵a, b, c, d?R+ ∴1 < m < 2 即原式成立例1小结(1)所谓放缩法就是利用不等式的传递性,对照证题目标进行合情合理的放大和缩小的过程。
(2)所谓放缩的技巧:即对欲证 ,寻找一个(或多个)中间变量C,使 ,由A到C叫做“放”,由B到C叫做“缩”。
(3)使用放缩法证题时要注意放和缩的“度”,否则就不能同向传递了。
(4)分式放缩:一个分式若分子变大则分式值变大,若分母变大则分式值变小,一个真分式,分子、分母同时加上同一个正数则分式值变大,利用这些性质,可达到证题目的。
变式练习11.已知a、b、c为三角形的三边,
求证: 【典型例题】 例2. :已知n∈N*,求 例2小结若欲证不等式含有与自然数n有关的n项和,可采用数列中裂项求和等方法来解题。
方法:裂项放缩
变式练习2【变式】例3、巳知:a、b、c∈ ,求证:略解【典型例题】例3小结
“添舍”放缩:
通过对不等式的一边进行添项或减项以达到解题目的,这是常规思路。
变式练习3 已知a,b,c不全为零,求证:【典型例题】 例4 : 求证:lg3 ·lg33<1 例4小结方法:公式放缩
利用已知的公式或恒不等式,把欲证不等式变形后再放缩,可获简解。
变式练习4 1、当 n > 2 时,求证: 证:∵n > 2 ∴ ∴n > 2时, 课堂小结1、用“放缩法”证明不等式的关键在于根据问题的特征选择恰当的方法,有时还需要几种方法融为一体。
2、在证明过程中,适当地进行放缩,可以化繁为简、化难为易,达到事半功倍的效果。但放缩的范围较难把握,常常出现放缩后得不出结论或得到相反的现象。因此,使用放缩法时,如何确定放缩目标尤为重要。要想正确确定放缩目标,就必须根据欲证结论,抓住题目的特点。
课堂小结3、掌握放缩技巧,真正做到弄懂弄通,并且还要根据不同题目的类型,采用恰到好处的放缩方法,才能把题解活,从而培养和提高自己的思维和逻辑推理能力,分析问题和解决问题的能力。谢谢啦
