2.1.1 平面上的柯西不等式的代数和向量形式
文档属性
| 名称 | 2.1.1 平面上的柯西不等式的代数和向量形式 |

|
|
| 格式 | zip | ||
| 文件大小 | 483.6KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-04 00:00:00 | ||
图片预览







文档简介
课件26张PPT。 2.1.1平面上的柯西不等式的代数和向量形式 大数学家柯西(Cauchy) 法国数学家、力学家。1789年8月
21日生于巴黎,1857年5月23日卒于索镇。曾为巴黎综合工科学校教授,当选为法国科学院院士。曾任国王查理十世的家庭教师。 柯西在大学期间,就开始研读拉格朗日和拉普拉斯的著作。柯西最重要的数学贡献在微积分、复变函数和微分方程等方面。
此外,柯西对力学和天文学也有许多贡献。著作甚丰,共出版了七部著作和800多篇论文,1882年开始出版他的全集,至1970年已达27卷之多。他的临终名言
是“人总是要死的,但是,他们的业绩永存”
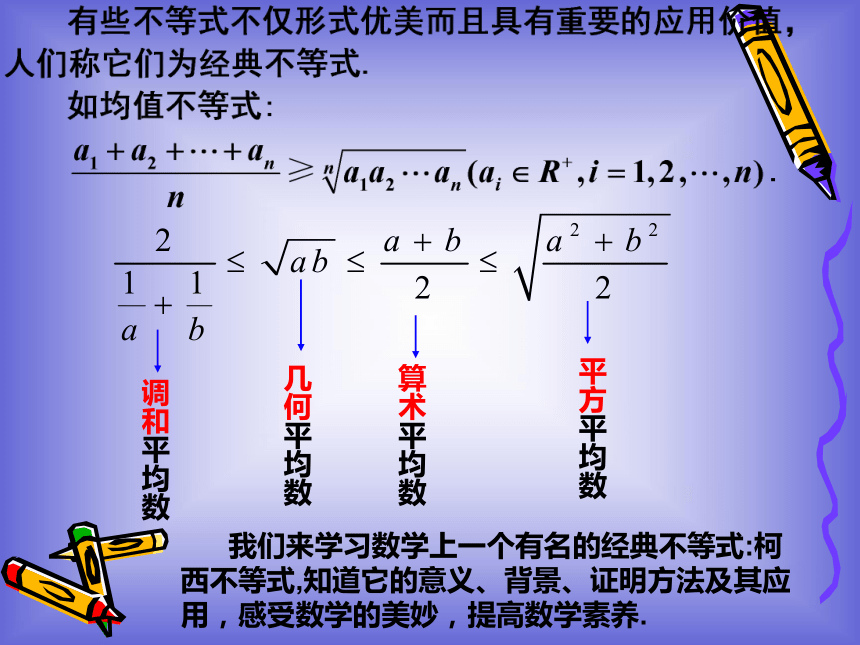
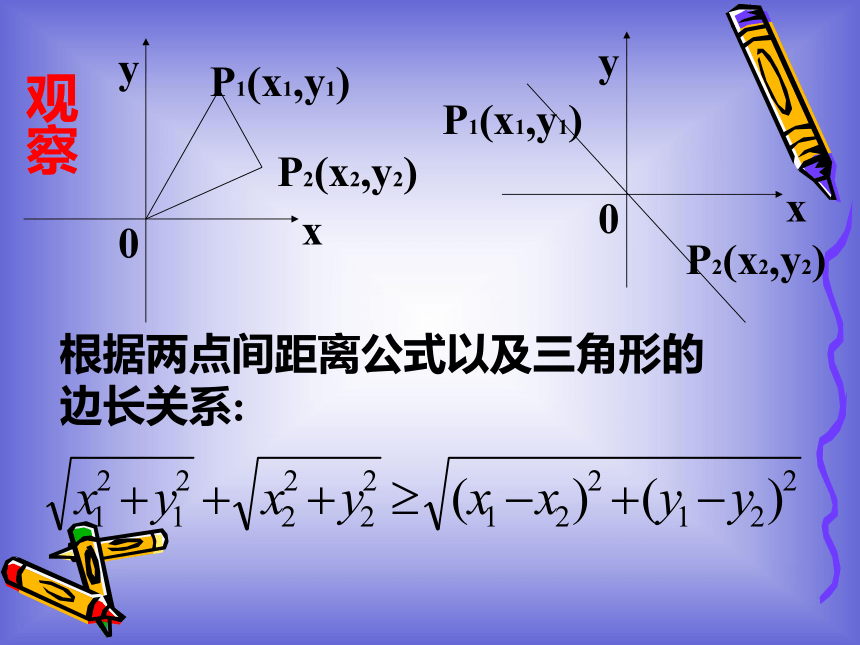
我们来学习数学上一个有名的经典不等式:柯西不等式,知道它的意义、背景、证明方法及其应用,感受数学的美妙,提高数学素养.定理1(二维形式的柯西不等式):你能证明吗?|ac+bd||ac|+|bd|柯西不等式的推论:探究:柯西不等式的几何意义是什么?|α||β|零向量根据两点间距离公式以及三角形的边长关系:观察[小问题·大思维]提示:当且仅当P1(x1,y1),P2(x2,y2),O(0,0)三点共线,且P1,P2在原点两旁时,等号成立.[方法总结][变式训练][方法总结] 利用柯西不等式证明某些不等式时,有时需要将数学表达式适当的变形.这种变形往往要求具有很高的技巧,必须善于分析题目的特征,根据题设条件,综合地利用添、拆、分解、组合、配方、变量代换、数形结合等方法才能发现问题的本质,找到突破口.[变式训练][例3] 若3x+4y=2,求x2+y2的最小值.[方法总结] 利用柯西不等式求最值的方法
(1)先变形凑成柯西不等式的结构特征,是利用柯西不等式求解的先决条件;
(2)有些最值问题从表面上看不能利用柯西不等式,但只要适当添加上常数项或为常数的各项,就可以应用柯西不等式来解,这也是运用柯西不等式解题的技巧;
(3)而有些最值问题的解决需要反复利用柯西不等式才能达到目的,但在运用过程中,每运用一次前后等号成立的条件必须一致,不能自相矛盾,否则就会出现错误.多次反复运用柯西不等式的方法也是常用的技巧之一.?[变式训练]3.如何把一条长为m的绳子截成3段,各围成一个正方
形,使这3个正方形的面积和最小?[考题检测] (2016·郑州模拟)已知实数a、b、c、d满足a2+b2=1,
c2+d2=2,求ac+bd的最大值.
[命题立意] 本题考查柯西不等式在求最值中的应用.课后作业:
课本:P34 T1,T3,T4思考:
问题1:还有没有其他方法来证明柯西不等式的二维形式?
问题2:柯西不等式的三维、四维、n维的形式是怎样的?如何推导?
21日生于巴黎,1857年5月23日卒于索镇。曾为巴黎综合工科学校教授,当选为法国科学院院士。曾任国王查理十世的家庭教师。 柯西在大学期间,就开始研读拉格朗日和拉普拉斯的著作。柯西最重要的数学贡献在微积分、复变函数和微分方程等方面。
此外,柯西对力学和天文学也有许多贡献。著作甚丰,共出版了七部著作和800多篇论文,1882年开始出版他的全集,至1970年已达27卷之多。他的临终名言
是“人总是要死的,但是,他们的业绩永存”
我们来学习数学上一个有名的经典不等式:柯西不等式,知道它的意义、背景、证明方法及其应用,感受数学的美妙,提高数学素养.定理1(二维形式的柯西不等式):你能证明吗?|ac+bd||ac|+|bd|柯西不等式的推论:探究:柯西不等式的几何意义是什么?|α||β|零向量根据两点间距离公式以及三角形的边长关系:观察[小问题·大思维]提示:当且仅当P1(x1,y1),P2(x2,y2),O(0,0)三点共线,且P1,P2在原点两旁时,等号成立.[方法总结][变式训练][方法总结] 利用柯西不等式证明某些不等式时,有时需要将数学表达式适当的变形.这种变形往往要求具有很高的技巧,必须善于分析题目的特征,根据题设条件,综合地利用添、拆、分解、组合、配方、变量代换、数形结合等方法才能发现问题的本质,找到突破口.[变式训练][例3] 若3x+4y=2,求x2+y2的最小值.[方法总结] 利用柯西不等式求最值的方法
(1)先变形凑成柯西不等式的结构特征,是利用柯西不等式求解的先决条件;
(2)有些最值问题从表面上看不能利用柯西不等式,但只要适当添加上常数项或为常数的各项,就可以应用柯西不等式来解,这也是运用柯西不等式解题的技巧;
(3)而有些最值问题的解决需要反复利用柯西不等式才能达到目的,但在运用过程中,每运用一次前后等号成立的条件必须一致,不能自相矛盾,否则就会出现错误.多次反复运用柯西不等式的方法也是常用的技巧之一.?[变式训练]3.如何把一条长为m的绳子截成3段,各围成一个正方
形,使这3个正方形的面积和最小?[考题检测] (2016·郑州模拟)已知实数a、b、c、d满足a2+b2=1,
c2+d2=2,求ac+bd的最大值.
[命题立意] 本题考查柯西不等式在求最值中的应用.课后作业:
课本:P34 T1,T3,T4思考:
问题1:还有没有其他方法来证明柯西不等式的二维形式?
问题2:柯西不等式的三维、四维、n维的形式是怎样的?如何推导?
