2.1.2 柯西不等式的一般形式及其参数配方法的证明
文档属性
| 名称 | 2.1.2 柯西不等式的一般形式及其参数配方法的证明 |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-04 11:37:57 | ||
图片预览








文档简介
课件27张PPT。新课导入回顾旧知1.二维形式的柯西不等式的代数形式?若a1,a2,b1,b2都是实数,
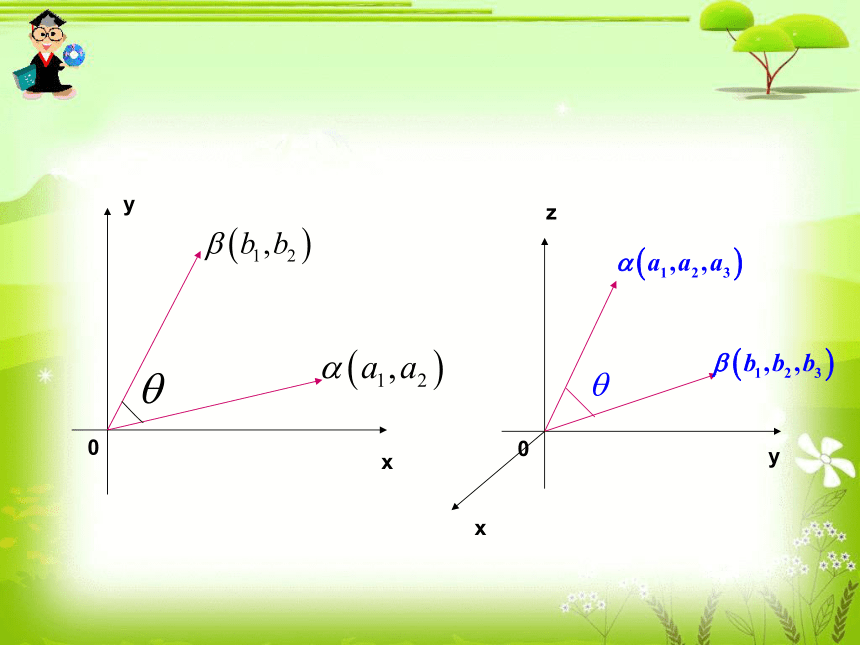
则(a12+a22)(b12+b22)≥(a1b1+a2b2)2,当且仅当a1b2=a2b1时,等号成立.2.二维形式的柯西不等式的向量形式? 设αβ是两个向量,则│α.β│≤│α││β│,当且仅当β是零向量,或存在实数k,使α=kβ时,等号成立. 从三维的角度思考问题,关于柯西不等式会有什么结论(结合图像)?思考 观察图,从平面向量的集合背景可以得到二维形式的柯西不等式.类似地,从空间向量的集合背景也可以得到│α.β│≤│α││β│ 将空间向量的坐标代入,化简得(a12+a22+a32)(b12+b22+b32)≥(a1b1+a2b2+a3b3)2,当且仅当α=β共线时,即β=0.或存在一个数k,使得α=kβ时,等号成立. 对比二维形式和三维形式的柯西不等式,你能猜想出一般形式的柯西不等式吗?2.1.2柯西不等式的一般形式
及其参数配方法的证明柯西不等式的一般形式为(a12+a22+…+an2)(b12+b22+…+bn2)≥(a1b1+a2b2
+…+anbn)2 (*)猜 想分 析如果设A=a12+a22+…+an2,B=a1b1+a2b2+…+anbn,C=b12+b22+…+bn2,不等式(*)就是AC≥B2.我们可以构造二次函数,通过讨论相应的判别式来证明.当a1=a2=…=an=0或b1=b2=…=bn=0时,(2)式显然成立.设a1,a2,…,an中至少有一个不为0,则a12+a22+…+an2>0.因为对于任意实数x,f(x)=(a1x+b1)2+(a2x+b2)2+…+(anx+bn)2≥0,所以二次函数f(x)的判别式△≤0,即4(a1b1+a2b2+…+anbn)-4(a12+a22+…+an2)(b12+b22+…+bn2)≤0.于是(a12+a22+…+an2)(b12+b22+…+bn2)≥(a1b1+a2b2+…+anbn)2,当且仅当f(x)有唯一零点时,判别式△=0,以上不等式取等号.此时,有唯一实数x0,使aix0+bi=0(i=1,2,…,n).若x0=0,则b1=b2=…=bn=0,(*)式成立;
若x0≠0,则有 ,总之,当且仅
当bi=0(i=1,2,…,n)或ai=kbi(i=1,2,…,n)时,等号成立.结论定理(一般形式的柯西不等式) 设a1,a2,…,an,b1,b2,…,bn都是实数,则(a12+a22+…+an2)(b12+b22+…+bn2) ≥(a1b1+a2b2+…+anbn)2,当且仅当bi=0(i=1,2,…,n)或存在一个数k,使得ai=kbi(i=1,2,…,n)时,等号成立.分析 用n乘要证的式子两边,能使式子变成明显符合柯西不等式的形式.根据柯西不等式,有(12+12+…+12)(a12+a22+…+an2)
≥(1×a1+ 1×a2+…+ 1×an)2,
所以n(a12+a22+…+an2) ≥(a1+a2+…+an)2
即已知a,b,c,d是不全相等的正数,证明a2+b2+c2+d2>ab+bc+cd+da.分析 上式两边都是a,b,c,d这四个数组成的式子,特别是右边式子的字母排列顺序启发我们,可以用柯西不等式进行证明.
分析 由x+2y+3z=1以及 x2+y2+z2 的形式,联系柯西不等式,可以通过构造(12+22+32)作为一个因式而解决问题.已知x+2y+3z=1以及 x2+y2+z2 的最小值.解:1.设x,y,z为正实数,且x+y+z=1,
求 的最小值2.已知x+y+z= ,求m=x2+2y2+z2的最小值。3.已知a,b,c为正实数,且
a+2b+3c=9,求 的最大值课堂小结1.一般形式的柯西不等式:设a1,a2,…,an,b1,b2,…,bn都是实数,则(a12+a22+…+an2)(b12+b22+…+bn2) ≥(a1b1+a2b2+…+anbn)2,当且仅当bi=0(i=1,2,…,n)或存在一个数k,使得ai=kbi(i=1,2,…,n)时,等号成立.2.一般形式的柯西不等式的应用. 对于许多不等式问题,应用柯西不等式往往简明。掌握柯西不等式的结构特点,灵活应用.随堂练习1.已知a,b,c,d∈R+,且a+b+c+d=1,
求证a2+b2+c2+d2≥
则(a12+a22)(b12+b22)≥(a1b1+a2b2)2,当且仅当a1b2=a2b1时,等号成立.2.二维形式的柯西不等式的向量形式? 设αβ是两个向量,则│α.β│≤│α││β│,当且仅当β是零向量,或存在实数k,使α=kβ时,等号成立. 从三维的角度思考问题,关于柯西不等式会有什么结论(结合图像)?思考 观察图,从平面向量的集合背景可以得到二维形式的柯西不等式.类似地,从空间向量的集合背景也可以得到│α.β│≤│α││β│ 将空间向量的坐标代入,化简得(a12+a22+a32)(b12+b22+b32)≥(a1b1+a2b2+a3b3)2,当且仅当α=β共线时,即β=0.或存在一个数k,使得α=kβ时,等号成立. 对比二维形式和三维形式的柯西不等式,你能猜想出一般形式的柯西不等式吗?2.1.2柯西不等式的一般形式
及其参数配方法的证明柯西不等式的一般形式为(a12+a22+…+an2)(b12+b22+…+bn2)≥(a1b1+a2b2
+…+anbn)2 (*)猜 想分 析如果设A=a12+a22+…+an2,B=a1b1+a2b2+…+anbn,C=b12+b22+…+bn2,不等式(*)就是AC≥B2.我们可以构造二次函数,通过讨论相应的判别式来证明.当a1=a2=…=an=0或b1=b2=…=bn=0时,(2)式显然成立.设a1,a2,…,an中至少有一个不为0,则a12+a22+…+an2>0.因为对于任意实数x,f(x)=(a1x+b1)2+(a2x+b2)2+…+(anx+bn)2≥0,所以二次函数f(x)的判别式△≤0,即4(a1b1+a2b2+…+anbn)-4(a12+a22+…+an2)(b12+b22+…+bn2)≤0.于是(a12+a22+…+an2)(b12+b22+…+bn2)≥(a1b1+a2b2+…+anbn)2,当且仅当f(x)有唯一零点时,判别式△=0,以上不等式取等号.此时,有唯一实数x0,使aix0+bi=0(i=1,2,…,n).若x0=0,则b1=b2=…=bn=0,(*)式成立;
若x0≠0,则有 ,总之,当且仅
当bi=0(i=1,2,…,n)或ai=kbi(i=1,2,…,n)时,等号成立.结论定理(一般形式的柯西不等式) 设a1,a2,…,an,b1,b2,…,bn都是实数,则(a12+a22+…+an2)(b12+b22+…+bn2) ≥(a1b1+a2b2+…+anbn)2,当且仅当bi=0(i=1,2,…,n)或存在一个数k,使得ai=kbi(i=1,2,…,n)时,等号成立.分析 用n乘要证的式子两边,能使式子变成明显符合柯西不等式的形式.根据柯西不等式,有(12+12+…+12)(a12+a22+…+an2)
≥(1×a1+ 1×a2+…+ 1×an)2,
所以n(a12+a22+…+an2) ≥(a1+a2+…+an)2
即已知a,b,c,d是不全相等的正数,证明a2+b2+c2+d2>ab+bc+cd+da.分析 上式两边都是a,b,c,d这四个数组成的式子,特别是右边式子的字母排列顺序启发我们,可以用柯西不等式进行证明.
分析 由x+2y+3z=1以及 x2+y2+z2 的形式,联系柯西不等式,可以通过构造(12+22+32)作为一个因式而解决问题.已知x+2y+3z=1以及 x2+y2+z2 的最小值.解:1.设x,y,z为正实数,且x+y+z=1,
求 的最小值2.已知x+y+z= ,求m=x2+2y2+z2的最小值。3.已知a,b,c为正实数,且
a+2b+3c=9,求 的最大值课堂小结1.一般形式的柯西不等式:设a1,a2,…,an,b1,b2,…,bn都是实数,则(a12+a22+…+an2)(b12+b22+…+bn2) ≥(a1b1+a2b2+…+anbn)2,当且仅当bi=0(i=1,2,…,n)或存在一个数k,使得ai=kbi(i=1,2,…,n)时,等号成立.2.一般形式的柯西不等式的应用. 对于许多不等式问题,应用柯西不等式往往简明。掌握柯西不等式的结构特点,灵活应用.随堂练习1.已知a,b,c,d∈R+,且a+b+c+d=1,
求证a2+b2+c2+d2≥
