3.1.1 数学归纳法原理课件17张PPT
文档属性
| 名称 | 3.1.1 数学归纳法原理课件17张PPT |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标B版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-04 00:00:00 | ||
图片预览






文档简介
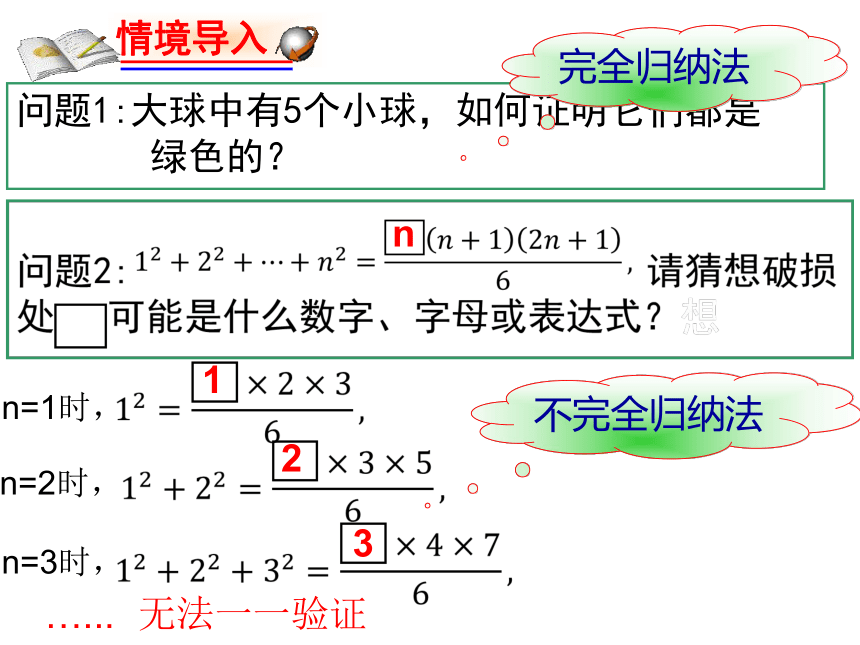
课件17张PPT。数学归纳法问题1:大球中有5个小球,如何证明它们都是
绿色的? 完全归纳法 ???n=1时,n=2时,??n=3时,123n不完全归纳法 …...无法一一验证看看下面的动画对我们解决问题有什么启示?问:多米诺骨牌能全部倒下,必须具备什么条件?(1)第一块骨牌倒下;(2)前一块倒下必导致后一块倒下。 条件(2)给出了一个递推关系,假设第K块倒下,则一定导致后一块即第K+1块也倒下.(1)第1块骨牌倒下。(1)当n=1时,验证猜想正确。(2)如果第k块倒下时,
一定能导致第k+1块也倒下。(2)如果n=k 时猜想成立 根据(1)和(2),可知不论有
多少个骨牌都能全部倒下。 根据(1)和(2),可知对所有的正
整数n,猜想都成立。一定能推出当n=k+1时猜想也成立多米诺骨牌游戏原理通过有限个步骤的推理,
证n取所有正整数都成立?数学归纳法 一般地,证明一个与正整数n有关的命题,可按下列步骤进行:(1)证明当n取第一个值n0时命题成立,
(2)假设当n=k(k∈N* ,k≥ n0)时命题成立,
证明当n=k+1时命题也成立,
只要完成这两个步骤,就可以断定命题从n0开始的所有正整数n都成立.
这种证明方法叫做 数学归纳法?总结:
在运用数学归纳法证明数学问题时,起始项不一定是n=1开始,需要“找准起点,奠基要稳”。?证明:(1)当n=1时,??即n=1时,等式成立.??????证明:(1)当n=1时,??即n=1时,等式成立.???????????∴由(1)(2)可得,等式成立?用数学归纳法证明:(n?N*)用数学归纳法证明:证明:当n=k+1时(2)假设当n=k (k?N*)时,等式成立,即(1)当n=1时,(n?N*)左边=等比数列求和!=右边,即当n=k+1时等式也成立。根据(1)和(2)可知,等式对任何n?N*成立。错解!错因:没有用到假设!左边=1,右边=1,等式成立。用数学归纳法证明:证明:当n=k+1时假设当n=k (k?N*)时,等式成立,即(n?N*)左边==右边,即当n=k+1时等式也成立。∴等式对任何n?N*成立。错解!错因:没有归纳奠基问题:你能得到什么猜想?猜想:用数学归纳法证明,问题:初始值从 取起.5计算:求证:2证明:命题成立。命题成立,命题成立。 大于?证明目标数学归纳法验证n=n0 时
命题成立课堂小结 若n = k ( k ≥ n0) 时命题成
立 n=k+1时命题也成立 命题对所有的正整数n ( n ≥ n0)都成立。归纳奠基归纳递推两个步骤,一个结论。结论用“有限”步骤解决“无限”验证
再 见
绿色的? 完全归纳法 ???n=1时,n=2时,??n=3时,123n不完全归纳法 …...无法一一验证看看下面的动画对我们解决问题有什么启示?问:多米诺骨牌能全部倒下,必须具备什么条件?(1)第一块骨牌倒下;(2)前一块倒下必导致后一块倒下。 条件(2)给出了一个递推关系,假设第K块倒下,则一定导致后一块即第K+1块也倒下.(1)第1块骨牌倒下。(1)当n=1时,验证猜想正确。(2)如果第k块倒下时,
一定能导致第k+1块也倒下。(2)如果n=k 时猜想成立 根据(1)和(2),可知不论有
多少个骨牌都能全部倒下。 根据(1)和(2),可知对所有的正
整数n,猜想都成立。一定能推出当n=k+1时猜想也成立多米诺骨牌游戏原理通过有限个步骤的推理,
证n取所有正整数都成立?数学归纳法 一般地,证明一个与正整数n有关的命题,可按下列步骤进行:(1)证明当n取第一个值n0时命题成立,
(2)假设当n=k(k∈N* ,k≥ n0)时命题成立,
证明当n=k+1时命题也成立,
只要完成这两个步骤,就可以断定命题从n0开始的所有正整数n都成立.
这种证明方法叫做 数学归纳法?总结:
在运用数学归纳法证明数学问题时,起始项不一定是n=1开始,需要“找准起点,奠基要稳”。?证明:(1)当n=1时,??即n=1时,等式成立.??????证明:(1)当n=1时,??即n=1时,等式成立.???????????∴由(1)(2)可得,等式成立?用数学归纳法证明:(n?N*)用数学归纳法证明:证明:当n=k+1时(2)假设当n=k (k?N*)时,等式成立,即(1)当n=1时,(n?N*)左边=等比数列求和!=右边,即当n=k+1时等式也成立。根据(1)和(2)可知,等式对任何n?N*成立。错解!错因:没有用到假设!左边=1,右边=1,等式成立。用数学归纳法证明:证明:当n=k+1时假设当n=k (k?N*)时,等式成立,即(n?N*)左边==右边,即当n=k+1时等式也成立。∴等式对任何n?N*成立。错解!错因:没有归纳奠基问题:你能得到什么猜想?猜想:用数学归纳法证明,问题:初始值从 取起.5计算:求证:2证明:命题成立。命题成立,命题成立。 大于?证明目标数学归纳法验证n=n0 时
命题成立课堂小结 若n = k ( k ≥ n0) 时命题成
立 n=k+1时命题也成立 命题对所有的正整数n ( n ≥ n0)都成立。归纳奠基归纳递推两个步骤,一个结论。结论用“有限”步骤解决“无限”验证
再 见
