人教版七年级上数学教学讲义,复习补习资料(含知识讲解,巩固练习):31【提高】《一元一次方程》全章复习与巩固含答案
文档属性
| 名称 | 人教版七年级上数学教学讲义,复习补习资料(含知识讲解,巩固练习):31【提高】《一元一次方程》全章复习与巩固含答案 |
|
|
| 格式 | zip | ||
| 文件大小 | 194.1KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-11-30 22:36:26 | ||
图片预览




文档简介
《一元一次方程》全章复习与巩固(提高)知识讲解
【学习目标】
1.理解方程,等式及一元一次方程的概念,并掌握它们的区别和联系;
2.会解一元一次方程,并理解每步变形的依据;
3.会根据实际问题列方程解应用题.
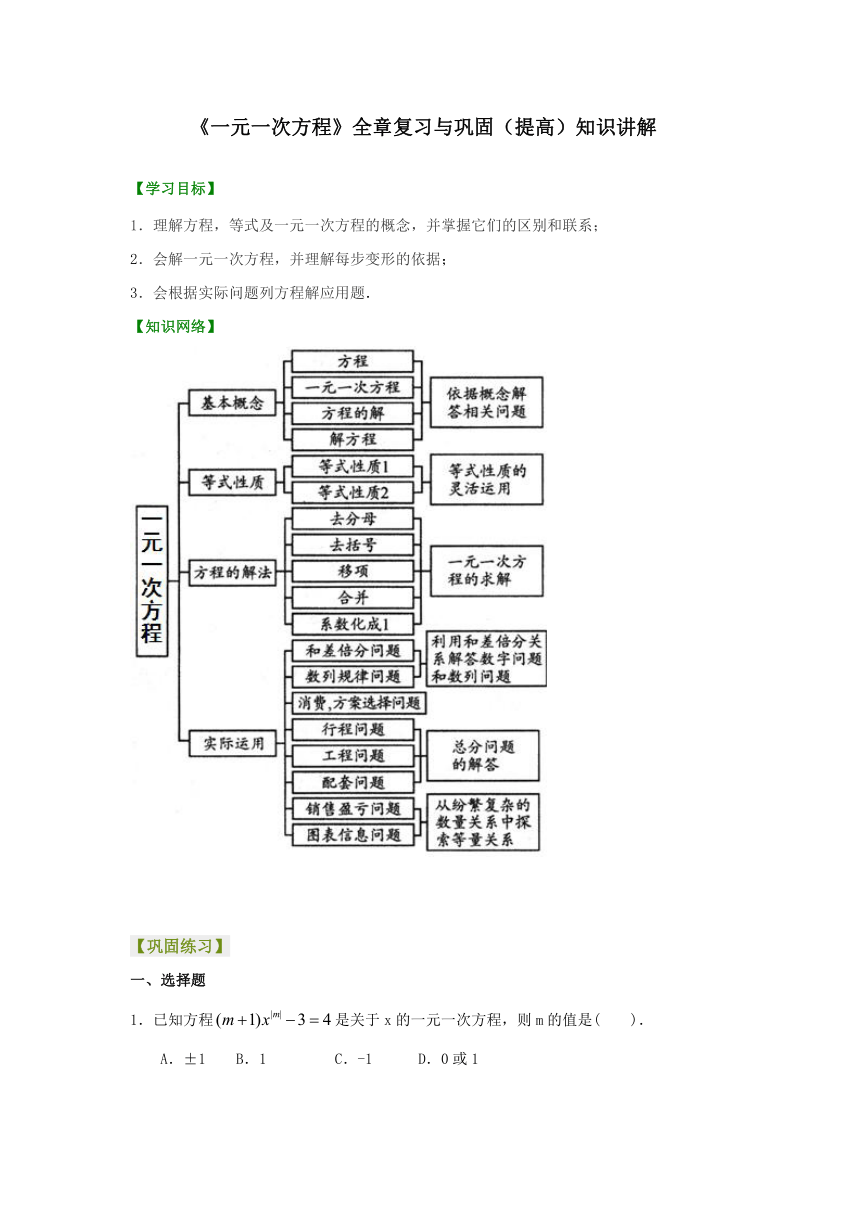
【知识网络】
/
【巩固练习】
一、选择题
1.已知方程/是关于x的一元一次方程,则m的值是( ).
A.±1 B.1 C.-1 D.0或1
2.已知/是方程/的解,那么关于y的方程/的解是( ).
A.y=1 B.y=-1 C.y=0 D.方程无解
3.已知/,则/等于( ).
A./ B./ C./ D./
4.(2019春?镇巴县校级月考)甲数是2013,甲数是乙数的/还多1.设乙数为x,则可列方程为( )
A.4(x﹣1)=2013 B.4x﹣1=2013 C. /x+1=2013 D. /(x+1)=2013
5.一架飞机在两城间飞行,顺风要5.5小时,逆风要6小时,风速为24千米/时,求两城距离x的方程是( )
A./ B./
C. / D./
6.某商场的老板销售一种商品,他要以不低于进价20%价格才能出售,但为了获得更多利润,他以高出进价80%的价格标价.若你想买下标价为360元的这种商品,最多降价多少时商店老板才能出售( )
A.80元 B.100元 C.120元 D.160元
7.某书中一道方程题:/,□处在印刷时被墨盖住了,查书后面的答案,得知这个方程的解是x=﹣2.5,那么□处应该是数字( ).
A.-2.5 B.2.5 C.5 D.7
8. 已知:/,/,/,/,…,
若/符合前面式子的规律,则a+b的值为( ).
A. 179 B. 140 C. 109 D. 210
二、填空题
9.已知方程/是关于x的一元一次方程,则这个方程的解为________.
10.已知/和/互为相反数,则/________.
11.当x=________时,代数式/的值为-1.
12.一商店把某商品按标价的九折出售仍可获得20%的利润率,若该商品的进价是每件30元,则标价是每件 元.
13.(2019?江西校级模拟)20××年3月份有5个星期六,它们的日期之和是80,若当月第三个星期六的日期为x,那么x= .
14.有一列数,按一定的规律排列:―1,2,―4,8,―16,32,―64,128,…,其中某三个相邻数之和为384,这三个数分别是 .
15.已知关于/的方程/和方程/有相同的解,则出该方程的解为 .
16.(2019春?南安市期中)方程|x﹣k|=1的一个解是x=2,那么k= .
三、解答题
17.解方程:
(1)/.
(2)/
(3)|3x-2|-4=0
18.(2019春?重庆校级月考)方程/和方程/的解相同,求a的值.
19.(2019?海淀区二模)小明坚持长跑健身.他从家匀速跑步到学校,通常需30分钟.某周日,小明与同学相约早上八点学校见,他七点半从家跑步出发,平均每分钟比平时快了40米,结果七点五十五分就到达了学校,求小明家到学校的距离.
20.商场计划拨款9万元,从厂家购进50台电视机,已知该厂家生产三种不同型号的电视机,出场价分别为甲种每台1500元,乙种每台2100元,丙种每台2500元.
(1)若商场同时购进其中两种不同型号的电视机共50台,用去9万元,请你研究一下商场的进货方案;(2)若商场销售一台甲种电视机可获利150元,销售一台乙种电视机可获利200元,销售一台丙种电视机可获利250元.在同时购进两种不同型号的电视机的方案中,为使销售时获利最多,该选择哪种进货方案?
【答案与解析】
一、选择题
1. 【答案】B
【解析】由题意得|m|=1,且m+1≠0,所以m=1,故选B.
2. 【答案】C
【解析】由x=1是方程/的解,可代入求出a的值,然后把a的值代入方程a(y+4)=2ay+4a中,求出y的值.
3. 【答案】D
【解析】由原式可得:/,将“/”看作整体,合并化简即可.
4.【答案】C.
【解析】设乙数为x,由题意得,/x+1=2013.故选C.
5. 【答案】A
【解析】解:∵两城距离为x,顺风要5.5小时,逆风要6小时,
∴顺风速度=/,逆风速度=/,
∵风速为24千米/时,
∴可列方程为:/
6.【答案】C
【解析】解:设最多降价x元时商店老板才能出售.则可得:/×(1+20%)+x=360
解得:x=120.
7.【答案】C
【解析】把x=-2.5代入方程,再把□当作未知数解方程即可.
8.【答案】C
【解析】观察规律可得b=10,a=b2-1=99,所以a+b=109.
二、填空题
9.【答案】x=1
【解析】首先将原方程整理成/的形式,由一元一次方程的定义可知,二次项系数为0,所以a=5,代入方程中即可求出x的值.
10.【答案】-8
【解析】两数互为相反数,则和为0,由非负数的性质可知m-n+4=0,且n-3=0.从而得m=-1,n=3.
11.【答案】/
【解析】由题意可得方程/,化简方程可解出/.
12.【答案】40
【解析】解:设标价为/元,则有/,解得:/
13.【答案】16.
【解析】根据当月第三个星期六的日期为x,依题意得:x﹣14+x﹣7+x+7+x+x+14=80
解得:x=16,即这个月第三个星期三是16号.
14.【答案】128,-256,512
【解析】通过观察可得:第/个数为:/,所以第9,10个数分别为:/,经检验满足题意.
15.【答案】/
【解析】分别解得这两个关于x的方程的解为/,/,由它们相等得/,代入其中一解可得答案.
16.【答案】1或3.
【解析】解:由题意得,|2﹣k|=1,
则2﹣k=1或2﹣k=﹣1,
解得,k=1或k=3.
故答案为:1或3.
三、解答题
17.【解析】
解:(1)整理,得/,
去分母,得/,
去括号,得/,
移项,得/,
合并,得/,
系数化为1,得/.
(2)原方程可化为:/
解得:x=/
(3)原式可化为:|3x-2|=4
由/,可得:/;由/,可得:/
所以原方程的解为:x=2,x=-/;
18. 【解析】
解:解方程/,
分母化为整数可得:/,
去分母,得:2(17﹣20x)﹣6=8+10x,
去括号,得:34﹣40x﹣6=8+10x,
移项、合并同类项,得:﹣50x=﹣20,
系数化为1,得:x=/,
根据题意,将x=/代入方程/,
得:/,
/,
/,
/,
a=/.
19.【解析】
解:设小明家到学校的距离为x米,
由题意,得/+40=/,
解得x=6000.
答:小明家到学校的距离为6000米.
20.【解析】
解:(1)①解:设购进甲种电视机/台,则购进乙种电视机(50-/)台,根据题意,得
1500/+2100(50-/)=90000.
解得: /=25,则50-/=25.
故第一种进货方案是购甲、乙两种型号的电视机各25台.
②设购进甲种电视机/台,则购进丙种电视机(50- /)台,根据题意,得
1500/+2500(50-/)=90000.
解得: /=35,则50-/=15.
故第二种进货方案是购进甲种电视机35台,丙种电视机15台.
③设购进乙种电视机/台,则购进丙种电视机(50-/)台,根据题意,得
2100/+2500(50-/)=90000.
解得: /=87.5(不合题意).
故此种方案不可行.
(2)上述的第一种方案可获利:150×25+200×25=8750元,
第二种方案可获利:150×35+250×15=9000元,
因为8750<9000,故应选择第二种进货方案.
【学习目标】
1.理解方程,等式及一元一次方程的概念,并掌握它们的区别和联系;
2.会解一元一次方程,并理解每步变形的依据;
3.会根据实际问题列方程解应用题.
【知识网络】
/
【巩固练习】
一、选择题
1.已知方程/是关于x的一元一次方程,则m的值是( ).
A.±1 B.1 C.-1 D.0或1
2.已知/是方程/的解,那么关于y的方程/的解是( ).
A.y=1 B.y=-1 C.y=0 D.方程无解
3.已知/,则/等于( ).
A./ B./ C./ D./
4.(2019春?镇巴县校级月考)甲数是2013,甲数是乙数的/还多1.设乙数为x,则可列方程为( )
A.4(x﹣1)=2013 B.4x﹣1=2013 C. /x+1=2013 D. /(x+1)=2013
5.一架飞机在两城间飞行,顺风要5.5小时,逆风要6小时,风速为24千米/时,求两城距离x的方程是( )
A./ B./
C. / D./
6.某商场的老板销售一种商品,他要以不低于进价20%价格才能出售,但为了获得更多利润,他以高出进价80%的价格标价.若你想买下标价为360元的这种商品,最多降价多少时商店老板才能出售( )
A.80元 B.100元 C.120元 D.160元
7.某书中一道方程题:/,□处在印刷时被墨盖住了,查书后面的答案,得知这个方程的解是x=﹣2.5,那么□处应该是数字( ).
A.-2.5 B.2.5 C.5 D.7
8. 已知:/,/,/,/,…,
若/符合前面式子的规律,则a+b的值为( ).
A. 179 B. 140 C. 109 D. 210
二、填空题
9.已知方程/是关于x的一元一次方程,则这个方程的解为________.
10.已知/和/互为相反数,则/________.
11.当x=________时,代数式/的值为-1.
12.一商店把某商品按标价的九折出售仍可获得20%的利润率,若该商品的进价是每件30元,则标价是每件 元.
13.(2019?江西校级模拟)20××年3月份有5个星期六,它们的日期之和是80,若当月第三个星期六的日期为x,那么x= .
14.有一列数,按一定的规律排列:―1,2,―4,8,―16,32,―64,128,…,其中某三个相邻数之和为384,这三个数分别是 .
15.已知关于/的方程/和方程/有相同的解,则出该方程的解为 .
16.(2019春?南安市期中)方程|x﹣k|=1的一个解是x=2,那么k= .
三、解答题
17.解方程:
(1)/.
(2)/
(3)|3x-2|-4=0
18.(2019春?重庆校级月考)方程/和方程/的解相同,求a的值.
19.(2019?海淀区二模)小明坚持长跑健身.他从家匀速跑步到学校,通常需30分钟.某周日,小明与同学相约早上八点学校见,他七点半从家跑步出发,平均每分钟比平时快了40米,结果七点五十五分就到达了学校,求小明家到学校的距离.
20.商场计划拨款9万元,从厂家购进50台电视机,已知该厂家生产三种不同型号的电视机,出场价分别为甲种每台1500元,乙种每台2100元,丙种每台2500元.
(1)若商场同时购进其中两种不同型号的电视机共50台,用去9万元,请你研究一下商场的进货方案;(2)若商场销售一台甲种电视机可获利150元,销售一台乙种电视机可获利200元,销售一台丙种电视机可获利250元.在同时购进两种不同型号的电视机的方案中,为使销售时获利最多,该选择哪种进货方案?
【答案与解析】
一、选择题
1. 【答案】B
【解析】由题意得|m|=1,且m+1≠0,所以m=1,故选B.
2. 【答案】C
【解析】由x=1是方程/的解,可代入求出a的值,然后把a的值代入方程a(y+4)=2ay+4a中,求出y的值.
3. 【答案】D
【解析】由原式可得:/,将“/”看作整体,合并化简即可.
4.【答案】C.
【解析】设乙数为x,由题意得,/x+1=2013.故选C.
5. 【答案】A
【解析】解:∵两城距离为x,顺风要5.5小时,逆风要6小时,
∴顺风速度=/,逆风速度=/,
∵风速为24千米/时,
∴可列方程为:/
6.【答案】C
【解析】解:设最多降价x元时商店老板才能出售.则可得:/×(1+20%)+x=360
解得:x=120.
7.【答案】C
【解析】把x=-2.5代入方程,再把□当作未知数解方程即可.
8.【答案】C
【解析】观察规律可得b=10,a=b2-1=99,所以a+b=109.
二、填空题
9.【答案】x=1
【解析】首先将原方程整理成/的形式,由一元一次方程的定义可知,二次项系数为0,所以a=5,代入方程中即可求出x的值.
10.【答案】-8
【解析】两数互为相反数,则和为0,由非负数的性质可知m-n+4=0,且n-3=0.从而得m=-1,n=3.
11.【答案】/
【解析】由题意可得方程/,化简方程可解出/.
12.【答案】40
【解析】解:设标价为/元,则有/,解得:/
13.【答案】16.
【解析】根据当月第三个星期六的日期为x,依题意得:x﹣14+x﹣7+x+7+x+x+14=80
解得:x=16,即这个月第三个星期三是16号.
14.【答案】128,-256,512
【解析】通过观察可得:第/个数为:/,所以第9,10个数分别为:/,经检验满足题意.
15.【答案】/
【解析】分别解得这两个关于x的方程的解为/,/,由它们相等得/,代入其中一解可得答案.
16.【答案】1或3.
【解析】解:由题意得,|2﹣k|=1,
则2﹣k=1或2﹣k=﹣1,
解得,k=1或k=3.
故答案为:1或3.
三、解答题
17.【解析】
解:(1)整理,得/,
去分母,得/,
去括号,得/,
移项,得/,
合并,得/,
系数化为1,得/.
(2)原方程可化为:/
解得:x=/
(3)原式可化为:|3x-2|=4
由/,可得:/;由/,可得:/
所以原方程的解为:x=2,x=-/;
18. 【解析】
解:解方程/,
分母化为整数可得:/,
去分母,得:2(17﹣20x)﹣6=8+10x,
去括号,得:34﹣40x﹣6=8+10x,
移项、合并同类项,得:﹣50x=﹣20,
系数化为1,得:x=/,
根据题意,将x=/代入方程/,
得:/,
/,
/,
/,
a=/.
19.【解析】
解:设小明家到学校的距离为x米,
由题意,得/+40=/,
解得x=6000.
答:小明家到学校的距离为6000米.
20.【解析】
解:(1)①解:设购进甲种电视机/台,则购进乙种电视机(50-/)台,根据题意,得
1500/+2100(50-/)=90000.
解得: /=25,则50-/=25.
故第一种进货方案是购甲、乙两种型号的电视机各25台.
②设购进甲种电视机/台,则购进丙种电视机(50- /)台,根据题意,得
1500/+2500(50-/)=90000.
解得: /=35,则50-/=15.
故第二种进货方案是购进甲种电视机35台,丙种电视机15台.
③设购进乙种电视机/台,则购进丙种电视机(50-/)台,根据题意,得
2100/+2500(50-/)=90000.
解得: /=87.5(不合题意).
故此种方案不可行.
(2)上述的第一种方案可获利:150×25+200×25=8750元,
第二种方案可获利:150×35+250×15=9000元,
因为8750<9000,故应选择第二种进货方案.
