4.1 几何图形(自主预习+课后集训+答案)
文档属性
| 名称 | 4.1 几何图形(自主预习+课后集训+答案) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.3MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 沪科版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-01 13:03:26 | ||
图片预览

文档简介
沪科版数学七年级上册同步课时训练
第4章 直线与角
4.1 几何图形
自主预习 基础达标
要点1 体、面、线、点
1. 长方体、正方体、圆柱、球都是几何体,几何体也简称为 ,包围着体的是 ,面有 的面和 的面两种.面和面相交的地方形成 ,线和线相交的地方形成 ,几何图形是由 、 、 、 组成的.用运动的观点来理解点、线、面、体,点动成 ,线动成 ,面动成 .
2. 几何图形包括 和 ,各个部分都在同一平面内的图形是 ,各个部分不都在同一平面内的图形是 .
要点2 常见几何体的分类、正多面体的有关概念
几何体的分类可以按照 、 和球体来分,或按照有无曲面来分: 和旋转体.
课后集训 巩固提升
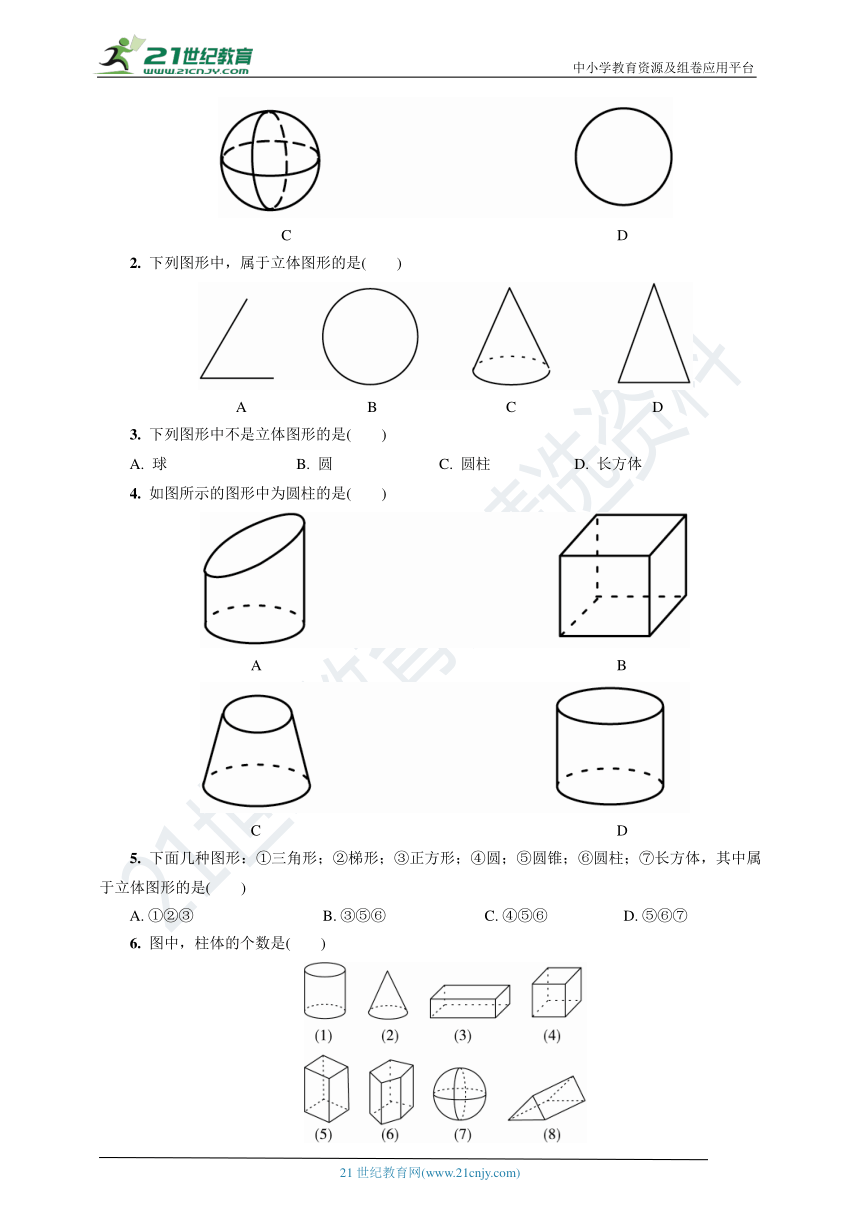
1. 下列图形中,是平面图形的是( )
A B
C D
2. 下列图形中,属于立体图形的是( )
A B C D
3. 下列图形中不是立体图形的是( )
A. 球 B. 圆 C. 圆柱 D. 长方体
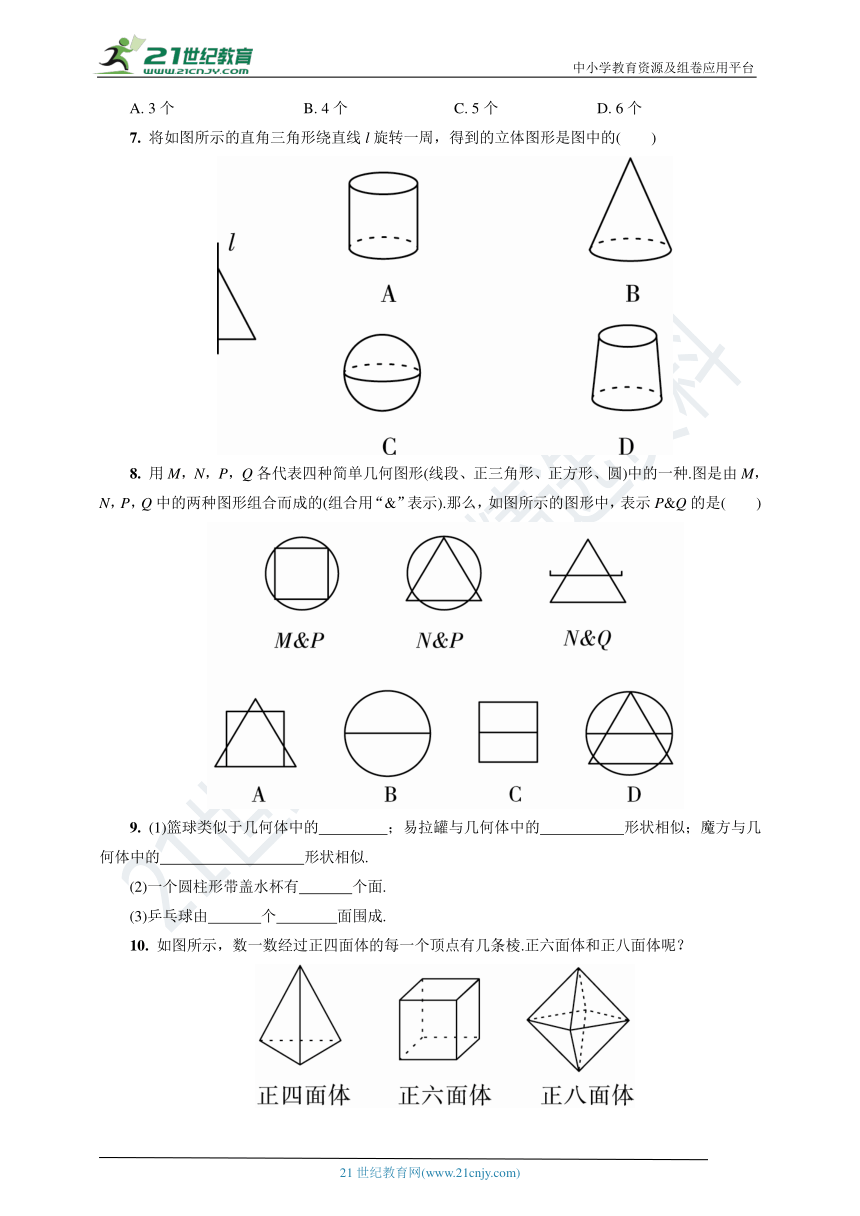
4. 如图所示的图形中为圆柱的是( )
A B
C D
5. 下面几种图形:①三角形;②梯形;③正方形;④圆;⑤圆锥;⑥圆柱;⑦长方体,其中属于立体图形的是( )
A. ①②③ B. ③⑤⑥ C. ④⑤⑥ D. ⑤⑥⑦
6. 图中,柱体的个数是( )
A. 3个 B. 4个 C. 5个 D. 6个
7. 将如图所示的直角三角形绕直线l旋转一周,得到的立体图形是图中的( )
8. 用M,N,P,Q各代表四种简单几何图形(线段、正三角形、正方形、圆)中的一种.图是由M,N,P,Q中的两种图形组合而成的(组合用“&”表示).那么,如图所示的图形中,表示P&Q的是( )
9. (1)篮球类似于几何体中的 ;易拉罐与几何体中的 形状相似;魔方与几何体中的 形状相似.
(2)一个圆柱形带盖水杯有 个面.
(3)乒乓球由 个 面围成.
10. 如图所示,数一数经过正四面体的每一个顶点有几条棱.正六面体和正八面体呢?
11. 观察图中的圆柱和棱柱,回答下列问题:
(1)棱柱和圆柱各由几个面组成?它们都是平面吗?
(2)圆柱的侧面与底面相交成几条线?它们都是直的吗?
(3)这个棱柱有几条棱?几个顶点?经过每个顶点有几条棱?
(4)通过对棱柱的观察,你能说出n棱柱的顶点数与n的关系及棱的条数与n的关系吗?
12. 十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(v)、面数(f)、棱数(e)之间存在的一个有趣的关系式,被称为欧拉公式.请你观察下列几种简单多面体模型,解答下列问题:
(1)根据上面多面体模型,完成表格中的空格:
多面体
顶点数(v)
面数(f)
棱数(e)
正四面体
4
4
正方体
8
6
正八面体
8
12
正十二面体
20
12
30
你发现顶点数(v)、面数(f)、棱数(e)之间存在的关系是 .
(2)一个多面体的面数比顶点数大8,且有30条棱,则这个多面体的面数是 .
(3)某个玻璃饰品的外形是简单多面体,它的外表面是由三角形和八边形两种多边形拼接而成,且有24个顶点,每个顶点处都有3条棱,设该多面体表面三角形的个数为x个,八边形的个数为y个,求x+y的值.
参考答案
自主预习 基础达标
要点1 1. 体 面 平 曲 线 点 点 线 面 体 线 面 体 2. 平面图形 立体图形 平面图形 立体图形
要点2 柱体 锥体 多面体
课后集训 巩固提升
1. D 2. C 3. B 4. D 5. D 6. D 7. B 8. B
9. (1)球体 圆柱体 正方体(正六面体) (2)3 (3)1 曲
10. 解:经过正四面体的每一个顶点有3条棱,经过正六面体的每一个顶点有3条棱,经过正八面体的每一个顶点有4条棱.
11. 解:(1)棱柱:8个面,圆柱:3个面;棱柱:都是平面,圆柱:2个平面、1个曲面.
(2)2条,不是.
(3)18条棱,12个顶点,经过每个顶点有3条棱.
(4)n棱柱顶点数是2n,棱的条数是3n.
12. 解:(1)6 12 6 v+f-e=2
(2)20
(3)由题意可知,其面数为x+y,顶点数为24,棱数为24×3÷2=36,所以24+(x+y)-36=2,即x+y=14.
第4章 直线与角
4.1 几何图形
自主预习 基础达标
要点1 体、面、线、点
1. 长方体、正方体、圆柱、球都是几何体,几何体也简称为 ,包围着体的是 ,面有 的面和 的面两种.面和面相交的地方形成 ,线和线相交的地方形成 ,几何图形是由 、 、 、 组成的.用运动的观点来理解点、线、面、体,点动成 ,线动成 ,面动成 .
2. 几何图形包括 和 ,各个部分都在同一平面内的图形是 ,各个部分不都在同一平面内的图形是 .
要点2 常见几何体的分类、正多面体的有关概念
几何体的分类可以按照 、 和球体来分,或按照有无曲面来分: 和旋转体.
课后集训 巩固提升
1. 下列图形中,是平面图形的是( )
A B
C D
2. 下列图形中,属于立体图形的是( )
A B C D
3. 下列图形中不是立体图形的是( )
A. 球 B. 圆 C. 圆柱 D. 长方体
4. 如图所示的图形中为圆柱的是( )
A B
C D
5. 下面几种图形:①三角形;②梯形;③正方形;④圆;⑤圆锥;⑥圆柱;⑦长方体,其中属于立体图形的是( )
A. ①②③ B. ③⑤⑥ C. ④⑤⑥ D. ⑤⑥⑦
6. 图中,柱体的个数是( )
A. 3个 B. 4个 C. 5个 D. 6个
7. 将如图所示的直角三角形绕直线l旋转一周,得到的立体图形是图中的( )
8. 用M,N,P,Q各代表四种简单几何图形(线段、正三角形、正方形、圆)中的一种.图是由M,N,P,Q中的两种图形组合而成的(组合用“&”表示).那么,如图所示的图形中,表示P&Q的是( )
9. (1)篮球类似于几何体中的 ;易拉罐与几何体中的 形状相似;魔方与几何体中的 形状相似.
(2)一个圆柱形带盖水杯有 个面.
(3)乒乓球由 个 面围成.
10. 如图所示,数一数经过正四面体的每一个顶点有几条棱.正六面体和正八面体呢?
11. 观察图中的圆柱和棱柱,回答下列问题:
(1)棱柱和圆柱各由几个面组成?它们都是平面吗?
(2)圆柱的侧面与底面相交成几条线?它们都是直的吗?
(3)这个棱柱有几条棱?几个顶点?经过每个顶点有几条棱?
(4)通过对棱柱的观察,你能说出n棱柱的顶点数与n的关系及棱的条数与n的关系吗?
12. 十八世纪瑞士数学家欧拉证明了简单多面体中顶点数(v)、面数(f)、棱数(e)之间存在的一个有趣的关系式,被称为欧拉公式.请你观察下列几种简单多面体模型,解答下列问题:
(1)根据上面多面体模型,完成表格中的空格:
多面体
顶点数(v)
面数(f)
棱数(e)
正四面体
4
4
正方体
8
6
正八面体
8
12
正十二面体
20
12
30
你发现顶点数(v)、面数(f)、棱数(e)之间存在的关系是 .
(2)一个多面体的面数比顶点数大8,且有30条棱,则这个多面体的面数是 .
(3)某个玻璃饰品的外形是简单多面体,它的外表面是由三角形和八边形两种多边形拼接而成,且有24个顶点,每个顶点处都有3条棱,设该多面体表面三角形的个数为x个,八边形的个数为y个,求x+y的值.
参考答案
自主预习 基础达标
要点1 1. 体 面 平 曲 线 点 点 线 面 体 线 面 体 2. 平面图形 立体图形 平面图形 立体图形
要点2 柱体 锥体 多面体
课后集训 巩固提升
1. D 2. C 3. B 4. D 5. D 6. D 7. B 8. B
9. (1)球体 圆柱体 正方体(正六面体) (2)3 (3)1 曲
10. 解:经过正四面体的每一个顶点有3条棱,经过正六面体的每一个顶点有3条棱,经过正八面体的每一个顶点有4条棱.
11. 解:(1)棱柱:8个面,圆柱:3个面;棱柱:都是平面,圆柱:2个平面、1个曲面.
(2)2条,不是.
(3)18条棱,12个顶点,经过每个顶点有3条棱.
(4)n棱柱顶点数是2n,棱的条数是3n.
12. 解:(1)6 12 6 v+f-e=2
(2)20
(3)由题意可知,其面数为x+y,顶点数为24,棱数为24×3÷2=36,所以24+(x+y)-36=2,即x+y=14.
同课章节目录
- 第1章 有理数
- 1.1 正数和负数
- 1.2 数轴、相反数和绝对值
- 1.3 有理数的大小
- 1.4 有理数的加减
- 1.5 有理数的乘除
- 1.6 有理数的乘方
- 1.7 近似数
- 第2章 整式加减
- 2.1 代数式
- 2.2 整式加减
- 第3章 一次方程与方程组
- 3.1 一元一次方程及其解法
- 3.2 一元一次方程的应用
- 3.3二元一次方程组及其解法
- 3.4 二元一次方程组的应用
- 3.5 三元一次方程组及其解法
- 第4章 直线与角
- 4.1 几何图形
- 4.2 线段、射线、直线
- 4.3 线段的 长短比较
- 4.4 角
- 4.5 角的比较与补(余)角
- 4.6 用尺规作线段与角
- 第5章 数据的收集与整理
- 5.1 数据的 收集
- 5.2 数据的整理
- 5.3 用统计图描述数据
- 5.4 从图表中的数据获取信息
