北师大版七年级上册 5.6 一元一次方程的应用之追赶小明课件(共26张PPT)
文档属性
| 名称 | 北师大版七年级上册 5.6 一元一次方程的应用之追赶小明课件(共26张PPT) |  | |
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-02 14:04:09 | ||
图片预览







文档简介
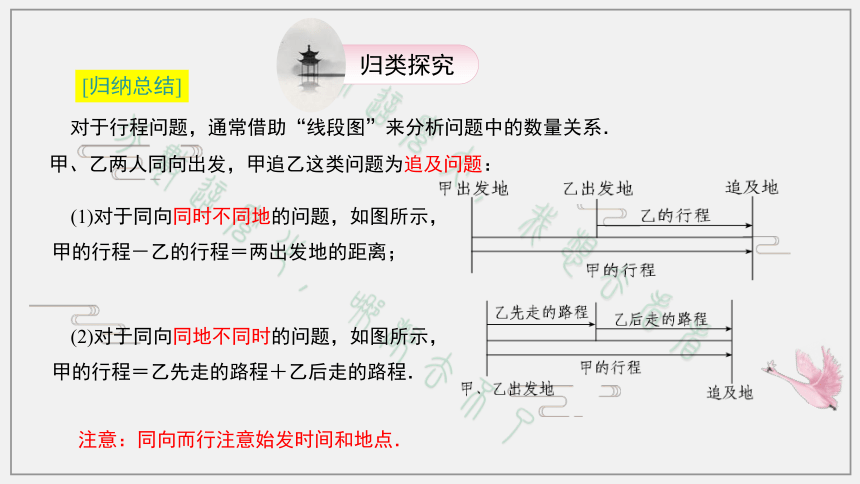
课件26张PPT。一元一次方程的应用之追赶小明第五章 一元一次方程目录当堂测评学习指南归类探究知识管理教学目标
借助“线段图”分析复杂问题中的数量关系,从而建立方程解决实际问题,进一步掌握列方程解应用题的步骤.发展分析问题、解决问题的能力,进一步体会方程模型的作用.
1.学会利用线段图分析行程问题,寻找等量关系,建立数学模型.(难点)
2.能利用行程中的速度、路程、时间之间的关系列方程解应用题.(重点)1.行程问题中常用的数量关系
基本关系:路程=速度×时间.
相遇问题:甲、乙相向而行,则甲走的路程+乙走的路程=总路程.
追及问题:甲、乙同向不同地,则后者走的路程=前者走的路程+两地间的距离.
2.环形跑道问题
数量关系:(1)甲、乙两人在环形跑道上同时同地同向出发,则快的必须多跑一圈才能追上慢的;
(2)甲、乙两人在环形跑道上同时同地反向出发,则两人首次相遇时所走的路程之和等于环形跑道一圈的长度.
3.航行问题
数量关系:(1)顺水速度=静水速度+水流速度;
(2)逆水速度=静水速度-水流速度;
(3)顺水速度-逆水速度=2×水速. [解析] 设妹妹用时x分钟,由路程相等列出方程
90×75×16=100×60×x,解得x=18.[归纳总结] 速度×时间=路程 类型一: 速度、路程、时间之间的关系 哥哥上学平均每分钟走90步,每步长75cm,用16分钟到学校,妹妹沿同一条路上学,每分米走100步,每步长60cm,则妹妹到校所用的时间是( )。
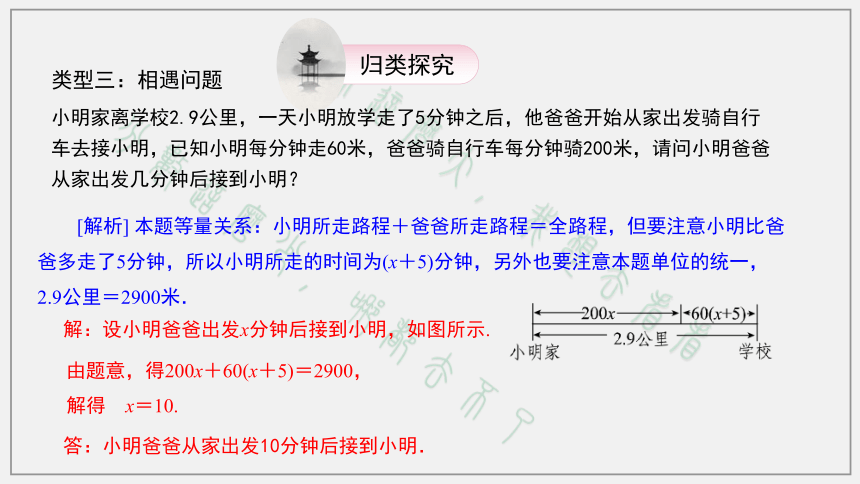
A.14 分钟 B.15分钟 C.18分钟 D.20分钟 一队学生去校外进行军事野营训练,他们以5 km/h的速度行进,走了18 min的时候,学校要将一个紧急通知传给队长,通讯员从学校出发,骑自行车以14 km/h的速度按原路追上去,通讯员用多少时间可以追上学生的队伍? 相等关系:通讯员的行进路程=学生的行进路程.18/60×55x14x类型二:追及问题(1)对于同向同时不同地的问题,如图所示,甲的行程-乙的行程=两出发地的距离;[归纳总结] 甲、乙两人同向出发,甲追乙这类问题为追及问题:(2)对于同向同地不同时的问题,如图所示,甲的行程=乙先走的路程+乙后走的路程.注意:同向而行注意始发时间和地点. 对于行程问题,通常借助“线段图”来分析问题中的数量关系. [解析] 本题等量关系:小明所走路程+爸爸所走路程=全路程,但要注意小明比爸爸多走了5分钟,所以小明所走的时间为(x+5)分钟,另外也要注意本题单位的统一,2.9公里=2900米.解:设小明爸爸出发x分钟后接到小明,如图所示.答:小明爸爸从家出发10分钟后接到小明.由题意,得200x+60(x+5)=2900,解得 x=10.类型三:相遇问题小明家离学校2.9公里,一天小明放学走了5分钟之后,他爸爸开始从家出发骑自行车去接小明,已知小明每分钟走60米,爸爸骑自行车每分钟骑200米,请问小明爸爸从家出发几分钟后接到小明? 两人从两地出发相向而行的行程问题称为相遇问题.[归纳总结]往往根据路程之和等于总路程列方程.如图所示,甲的行程+乙的行程=两地距离.类型之四 用一元一次方程解决航行问题
一架飞机在两个城市之间飞行,风速为24 km/h,顺风飞行需要2小时50分钟,逆风飞行需要3小时,求两城市之间的距离.
8x6x6048x6x604 4.A,B两地相距60千米,甲、乙两人分别从A,B两地出发相向而行,甲的速度是8千米/时,乙的速度是6千米/时.经过多长时间两人相距4千米?解:设走路快的人追上走路慢的人所用时间为t.
根据题意,得(100-60)t=100,解得t=2.5,
∴100t=100×2.5=250.
∴走路快的人要走250步才能追上走路慢的人. 5.[2018春·越秀区期末]我国古代数学著作《九章算术》中有这样一道题,原文是:“今有善行者行一百步,不善行者行六十步,今不善行者先行一百步,善行者追之,问几何步及之?”意思是:同样时间段内,走路快的人能走100步,走路慢的人只能走60步(两人的步长相同).走路慢的人先走100步,走路快的人要走多少步才能追上走路慢的人?(两人走的路线相同)试求解这个问题.6.(2019.六匐模拟)甲、乙两站间的路程为450 km.一列慢车从甲站开出,每小时行驶65 km,一列快车从乙站开出,每小时行驶85 km.
(1)两车同时开出,相向而行,多长时间相遇?
(2)快车先开30分钟,两车相向而行,慢车行驶多长时间后两车相遇?7.一列火车匀速行驶,经过一条长300 m的隧道需要20 s的时间.隧道的顶上有一盏灯,垂直向下发光,灯光照在火车上的时间是10 s.
(1)设火车的长度为x m,用含x的式子表示从车头经过灯下到车尾经过灯下火车所走的路程和这段时间内火车的平均速度;
(2)设火车的长度为x m,用含x的式子表示从车头进入隧道到车尾离开隧道火车所走的路程和这段时间内火车的平均速度;7.一列火车匀速行驶,经过一条长300 m的隧道需要20 s的时间.隧道的顶上有一盏灯,垂直向下发光,灯光照在火车上的时间是10 s.
(3)上述问题中火车的平均速度发生了变化吗?
(4)求这列火车的长度.
8.某行军队伍以7千米/时的速度行进,队尾的通讯员以11千米/时的速度赶到队伍前送一封信,送到后立即返回队尾,共用了13.2分钟,求这支队伍的长度.答:这支队伍的长度为0.72千米.答:A,B两地间的路程为108 km. 9.王力骑自行车从A地到B地,陈平骑自行车从B地到A地,两人都沿同一公路匀速前进,已知两人在上午8时同时出发,到上午10时,两人还相距36 km,到中午12时,两人又相距36 km.求A,B两地间的路程. 10.乙船航行于A,B两个码头之间,顺水航行需要3小时,逆水航行需要5小时,已知水流速度为4 km/h,求两码头之间的距离.答:A,B两码头之间距离是60千米.解:设爸爸x分钟能追赶上小明.
由题意得60(28+x)=200x,解得x=12.
因为200×12=2 400=2.4千米<2.7千米,
所以小解:设爸爸x分钟能追赶上小明.
由题意得60(28+x)=200x,解得x=12.
因为200×12=2 400=2.4千米<2.7千米,
所以小明爸爸能赶在小明到学校前把书送到小明手上.明爸爸能赶在小明到学校前把书送到小明手上. 11.小明家离学校2.7千米,一天早上上学,小明已走28分钟后,妈妈发现小明上学忘带数学书了,这时爸爸立即骑自行车带上数学书去追赶小明.已知小明上学每分钟走60米,爸爸骑车每分钟走200米,请问小明爸爸能否赶在小明到学校前把书送到小明手上? 12.小明早晨要在7:20以前赶到距家1000米的学校上学.一天,小明以80米/分钟的速度出发,5分钟后,小明的爸爸发现 他忘了带历史作业,于是,爸爸立即以180米/分钟的速度去追小明,并且在途中追上了他.(1)爸爸追上小明用了多长时间?
(2)追上小明时,距离学校还有多远?据题意,得 80×5+80x=180x. 答:爸爸追上小明用了4分钟.(2)180×4=720(米),1000-720=280(米).答:追上小明时,距离学校还有280米.解得 x=4.80×580x180x 分析:当爸爸追上小明时,两人所走路程相等.解:(1)设爸爸追上小明用了x分钟,则此题的数量关系可用线段图表示.13.甲、乙两人在一条长400 m的环形跑道上跑步,甲的速度是360 m/min,乙的速度是240 m/min.
(1)两人同时同地同向跑,问:第一次相遇时,两人一共跑了几圈?
(2)两人同时同地反向跑,问:几秒后两人第一次相遇?
借助“线段图”分析复杂问题中的数量关系,从而建立方程解决实际问题,进一步掌握列方程解应用题的步骤.发展分析问题、解决问题的能力,进一步体会方程模型的作用.
1.学会利用线段图分析行程问题,寻找等量关系,建立数学模型.(难点)
2.能利用行程中的速度、路程、时间之间的关系列方程解应用题.(重点)1.行程问题中常用的数量关系
基本关系:路程=速度×时间.
相遇问题:甲、乙相向而行,则甲走的路程+乙走的路程=总路程.
追及问题:甲、乙同向不同地,则后者走的路程=前者走的路程+两地间的距离.
2.环形跑道问题
数量关系:(1)甲、乙两人在环形跑道上同时同地同向出发,则快的必须多跑一圈才能追上慢的;
(2)甲、乙两人在环形跑道上同时同地反向出发,则两人首次相遇时所走的路程之和等于环形跑道一圈的长度.
3.航行问题
数量关系:(1)顺水速度=静水速度+水流速度;
(2)逆水速度=静水速度-水流速度;
(3)顺水速度-逆水速度=2×水速. [解析] 设妹妹用时x分钟,由路程相等列出方程
90×75×16=100×60×x,解得x=18.[归纳总结] 速度×时间=路程 类型一: 速度、路程、时间之间的关系 哥哥上学平均每分钟走90步,每步长75cm,用16分钟到学校,妹妹沿同一条路上学,每分米走100步,每步长60cm,则妹妹到校所用的时间是( )。
A.14 分钟 B.15分钟 C.18分钟 D.20分钟 一队学生去校外进行军事野营训练,他们以5 km/h的速度行进,走了18 min的时候,学校要将一个紧急通知传给队长,通讯员从学校出发,骑自行车以14 km/h的速度按原路追上去,通讯员用多少时间可以追上学生的队伍? 相等关系:通讯员的行进路程=学生的行进路程.18/60×55x14x类型二:追及问题(1)对于同向同时不同地的问题,如图所示,甲的行程-乙的行程=两出发地的距离;[归纳总结] 甲、乙两人同向出发,甲追乙这类问题为追及问题:(2)对于同向同地不同时的问题,如图所示,甲的行程=乙先走的路程+乙后走的路程.注意:同向而行注意始发时间和地点. 对于行程问题,通常借助“线段图”来分析问题中的数量关系. [解析] 本题等量关系:小明所走路程+爸爸所走路程=全路程,但要注意小明比爸爸多走了5分钟,所以小明所走的时间为(x+5)分钟,另外也要注意本题单位的统一,2.9公里=2900米.解:设小明爸爸出发x分钟后接到小明,如图所示.答:小明爸爸从家出发10分钟后接到小明.由题意,得200x+60(x+5)=2900,解得 x=10.类型三:相遇问题小明家离学校2.9公里,一天小明放学走了5分钟之后,他爸爸开始从家出发骑自行车去接小明,已知小明每分钟走60米,爸爸骑自行车每分钟骑200米,请问小明爸爸从家出发几分钟后接到小明? 两人从两地出发相向而行的行程问题称为相遇问题.[归纳总结]往往根据路程之和等于总路程列方程.如图所示,甲的行程+乙的行程=两地距离.类型之四 用一元一次方程解决航行问题
一架飞机在两个城市之间飞行,风速为24 km/h,顺风飞行需要2小时50分钟,逆风飞行需要3小时,求两城市之间的距离.
8x6x6048x6x604 4.A,B两地相距60千米,甲、乙两人分别从A,B两地出发相向而行,甲的速度是8千米/时,乙的速度是6千米/时.经过多长时间两人相距4千米?解:设走路快的人追上走路慢的人所用时间为t.
根据题意,得(100-60)t=100,解得t=2.5,
∴100t=100×2.5=250.
∴走路快的人要走250步才能追上走路慢的人. 5.[2018春·越秀区期末]我国古代数学著作《九章算术》中有这样一道题,原文是:“今有善行者行一百步,不善行者行六十步,今不善行者先行一百步,善行者追之,问几何步及之?”意思是:同样时间段内,走路快的人能走100步,走路慢的人只能走60步(两人的步长相同).走路慢的人先走100步,走路快的人要走多少步才能追上走路慢的人?(两人走的路线相同)试求解这个问题.6.(2019.六匐模拟)甲、乙两站间的路程为450 km.一列慢车从甲站开出,每小时行驶65 km,一列快车从乙站开出,每小时行驶85 km.
(1)两车同时开出,相向而行,多长时间相遇?
(2)快车先开30分钟,两车相向而行,慢车行驶多长时间后两车相遇?7.一列火车匀速行驶,经过一条长300 m的隧道需要20 s的时间.隧道的顶上有一盏灯,垂直向下发光,灯光照在火车上的时间是10 s.
(1)设火车的长度为x m,用含x的式子表示从车头经过灯下到车尾经过灯下火车所走的路程和这段时间内火车的平均速度;
(2)设火车的长度为x m,用含x的式子表示从车头进入隧道到车尾离开隧道火车所走的路程和这段时间内火车的平均速度;7.一列火车匀速行驶,经过一条长300 m的隧道需要20 s的时间.隧道的顶上有一盏灯,垂直向下发光,灯光照在火车上的时间是10 s.
(3)上述问题中火车的平均速度发生了变化吗?
(4)求这列火车的长度.
8.某行军队伍以7千米/时的速度行进,队尾的通讯员以11千米/时的速度赶到队伍前送一封信,送到后立即返回队尾,共用了13.2分钟,求这支队伍的长度.答:这支队伍的长度为0.72千米.答:A,B两地间的路程为108 km. 9.王力骑自行车从A地到B地,陈平骑自行车从B地到A地,两人都沿同一公路匀速前进,已知两人在上午8时同时出发,到上午10时,两人还相距36 km,到中午12时,两人又相距36 km.求A,B两地间的路程. 10.乙船航行于A,B两个码头之间,顺水航行需要3小时,逆水航行需要5小时,已知水流速度为4 km/h,求两码头之间的距离.答:A,B两码头之间距离是60千米.解:设爸爸x分钟能追赶上小明.
由题意得60(28+x)=200x,解得x=12.
因为200×12=2 400=2.4千米<2.7千米,
所以小解:设爸爸x分钟能追赶上小明.
由题意得60(28+x)=200x,解得x=12.
因为200×12=2 400=2.4千米<2.7千米,
所以小明爸爸能赶在小明到学校前把书送到小明手上.明爸爸能赶在小明到学校前把书送到小明手上. 11.小明家离学校2.7千米,一天早上上学,小明已走28分钟后,妈妈发现小明上学忘带数学书了,这时爸爸立即骑自行车带上数学书去追赶小明.已知小明上学每分钟走60米,爸爸骑车每分钟走200米,请问小明爸爸能否赶在小明到学校前把书送到小明手上? 12.小明早晨要在7:20以前赶到距家1000米的学校上学.一天,小明以80米/分钟的速度出发,5分钟后,小明的爸爸发现 他忘了带历史作业,于是,爸爸立即以180米/分钟的速度去追小明,并且在途中追上了他.(1)爸爸追上小明用了多长时间?
(2)追上小明时,距离学校还有多远?据题意,得 80×5+80x=180x. 答:爸爸追上小明用了4分钟.(2)180×4=720(米),1000-720=280(米).答:追上小明时,距离学校还有280米.解得 x=4.80×580x180x 分析:当爸爸追上小明时,两人所走路程相等.解:(1)设爸爸追上小明用了x分钟,则此题的数量关系可用线段图表示.13.甲、乙两人在一条长400 m的环形跑道上跑步,甲的速度是360 m/min,乙的速度是240 m/min.
(1)两人同时同地同向跑,问:第一次相遇时,两人一共跑了几圈?
(2)两人同时同地反向跑,问:几秒后两人第一次相遇?
同课章节目录
- 第一章 丰富的图形世界
- 1.1 生活中的立体图形
- 1.2 展开与折叠
- 1.3 截一个几何体
- 1.4 从三个不同方向看物体的形状
- 第二章 有理数及其运算
- 2.1 有理数
- 2.2 数轴
- 2.3 绝对值
- 2.4 有理数的加法
- 2.5 有理数的减法
- 2.6 有理数的加减混合运算
- 2.7 有理数的乘法
- 2.8 有理数的除法
- 2.9 有理数的乘方
- 2.10 科学记数法
- 2.11 有理数的混合运算
- 2.12 用计算器进行运算
- 第三章 整式及其加减
- 3.1 字母表示数
- 3.2 代数式
- 3.3 整式
- 3.4 整式的加减
- 3.5 探索与表达规律
- 第四章 基本平面图形
- 4.1 线段、射线、直线
- 4.2 比较线段的长短
- 4.3 角
- 4.4 角的比较
- 4.5 多边形和圆的初步认识
- 第五章 一元一次方程
- 5.1 认识一元一次方程
- 5.2 求解一元一次方程
- 5.3 应用一元一次方程——水箱变高了
- 5.4 应用一元一次方程——打折销售
- 5.5 应用一元一次方程——“希望工程”义演
- 5.6 应用一元一次方程——追赶小明
- 第六章 数据的收集与整理
- 6.1 数据的收集
- 6.2 普查和抽样调查
- 6.3 数据的表示
- 6.4 统计图的选择
