人教版八年级上数学教学讲义,复习补习资料(含知识讲解,巩固练习):15【基础】直角三角形全等判定含答案
文档属性
| 名称 | 人教版八年级上数学教学讲义,复习补习资料(含知识讲解,巩固练习):15【基础】直角三角形全等判定含答案 |  | |
| 格式 | zip | ||
| 文件大小 | 124.0KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-02 10:15:49 | ||
图片预览



文档简介
直角三角形全等判定(基础)
【学习目标】
1.理解和掌握判定直角三角形全等的一种特殊方法——“斜边,直角边”(即“HL”).
2.能熟练地用判定一般三角形全等的方法及判定直角三角形的特殊方法判定两个直角三角形全等.
【要点梳理】
【 直角三角形全等的判定,知识点讲解】
要点一、判定直角三角形全等的一般方法
由三角形全等的条件可知,对于两个直角三角形,满足一边一锐角对应相等,或两直角边对应相等,这两个直角三角形就全等了.这里用到的是“AAS”,“ASA”或“SAS”判定定理.
要点二、判定直角三角形全等的特殊方法——斜边,直角边定理
在两个直角三角形中,有斜边和一条直角边对应相等的两个直角三角形全等(可以简写成“斜边、直角边”或“HL”).这个判定方法是直角三角形所独有的,一般三角形不具备.
要点诠释:(1)“HL”从顺序上讲是“边边角”对应相等,由于其中含有直角这个特殊条件,所以三角形的形状和大小就确定了.
(2)判定两个直角三角形全等的方法共有5种:SAS、ASA、AAS、SSS、HL.证明两个直角三角形全等,首先考虑用斜边、直角边定理,再考虑用一般三角形全等的证明方法.
(3)应用“斜边、直角边”判定两个直角三角形全等的过程中要突出直角三角形这个条件,书写时必须在两个三角形前加上“Rt”.
【典型例题】
类型一、直角三角形全等的判定——“HL”
1、 已知:如图,AB⊥BD,CD⊥BD,AD=BC.
求证:(1)AB=CD:
(2)AD∥BC.
【思路点拨】先由“HL”证Rt△ABD≌Rt△CDB,再由内错角相等证两直线平行.
【答案与解析】
证明:(1)∵AB⊥BD,CD⊥BD,
∴∠ABD=∠CDB=90°
在Rt△ABD 和Rt△CDB中,
∴Rt△ABD≌Rt△CDB(HL)
∴AB=CD(全等三角形对应边相等)
(2)由∠ADB=∠CBD
∴AD∥BC .
【总结升华】证明两个直角三角形全等,首先考虑用斜边、直角边定理,再考虑用一般三角形全等的证明方法.
举一反三:
【 直角三角形全等的判定,例3】
【变式】已知:如图,AE⊥AB,BC⊥AB,AE=AB,ED=AC.
求证:ED⊥AC.
【答案】
证明:∵AE⊥AB,BC⊥AB,
∴∠DAE=∠CBA=90°
在Rt△DAE 与Rt△CBA中,
∴Rt△DAE≌Rt△CBA (HL)
∴∠E=∠CAB
∵∠CAB+∠EAF=90°,
∴∠E+∠EAF=90°,即∠AFE=90°
即ED⊥AC.
2、 判断满足下列条件的两个直角三角形是否全等,不全等的画“×”,全等的注明理由:
(1)一个锐角和这个角的对边对应相等;( )
(2)一个锐角和斜边对应相等; ( )
(3)两直角边对应相等; ( )
(4)一条直角边和斜边对应相等. ( )
【答案】(1)全等,“AAS”;(2)全等,“AAS”;(3)全等,“SAS”;(4)全等,“HL”.
【解析】理解题意,画出图形,根据全等三角形的判定来判断.
【总结升华】直角三角形全等可用的判定方法有5种:SAS、ASA、AAS、SSS、HL.
举一反三:
【变式】下列说法正确的有( )
(1)一个锐角及斜边对应相等的两个直角三角形全等;
(2)一个锐角及一条直角边对应相等的两个直角三角形全等;
(3)两个锐角对应等的两个直角三角形全等;
(4)有两条边相等的两个直角三角形全等;
(5)有斜边和一条直角边对应相等的两个直角三角形全等.
A.2个 B.3个 C.4个 D.5个
【答案】C.
解:(1)一个锐角及斜边对应相等的两个直角三角形全等,根据AAS可判定两个直角三角形全等;(2)一个锐角及一条直角边对应相等的两个直角三角形全等,根据AAS或ASA可判定两个直角三角形全等;(3)两个锐角对应等的两个直角三角形全等,缺少“边”这个条件,故不可判定两个直角三角形全等;(4)有两条边相等的两个直角三角形全等,根据SAS或HL可判定两个直角三角形全等;(5)有斜边和一条直角边对应相等的两个直角三角形全等,根据HL可判定两个直角三角形全等.所以说法正确的有4个.故选C.
3、(2019春?深圳校级月考)如图,AB⊥AC于A,BD⊥CD于D,若AC=DB,则下列结论中不正确的是( )
A.∠A=∠D B.∠ABC=∠DCB C.OB=OD D.OA=OD
【思路点拨】根据已知及全等三角形的判定方法进行分析,从而得到答案.做题时要结合已知条件与全等的判定方法逐一验证.
【答案与解析】
解:∵AB⊥AC于A,BD⊥CD于D
∴∠A=∠D=90°(A正确)
又∵AC=DB,BC=BC
∴△ABC≌△DCB(HL)
∴∠ABC=∠DCB(B正确)
∴AB=CD
又∵∠AOB=∠C
∴△AOB≌△DOC(AAS)
∴OA=OD(D正确)
C中OD、OB不是对应边,不相等.
故选C.
【总结升华】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
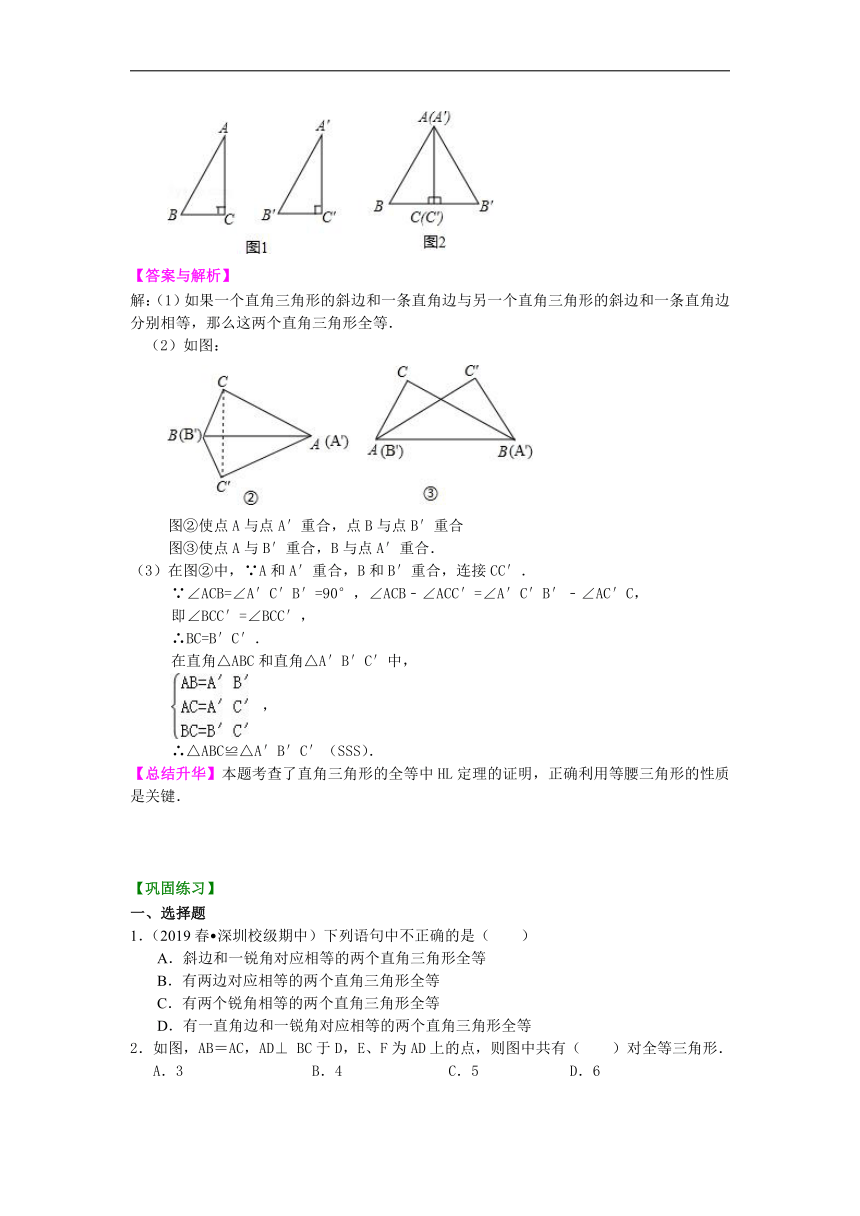
4、已知:如图1,在Rt△ABC和Rt△A′B′C′中,AB=A′B′,AC=A′C′,C=∠C′=90°
求证:Rt△ABC和Rt△A′B′C′全等.
(1)请你用“如果…,那么…”的形式叙述上述命题;
(2)将△ABC和△A′B′C′拼在一起,请你画出两种拼接图形;例如图2:(即使点A与点A′重合,点C与点C′重合.)
(3)请你选择你拼成的其中一种图形,证明该命题.
【答案与解析】
解:(1)如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边分别相等,那么这两个直角三角形全等.
(2)如图:
图②使点A与点A′重合,点B与点B′重合
图③使点A与B′重合,B与点A′重合.
(3)在图②中,∵A和A′重合,B和B′重合,连接CC′.
∵∠ACB=∠A′C′B′=90°,∠ACB﹣∠ACC′=∠A′C′B′﹣∠AC′C,
即∠BCC′=∠BCC′,
∴BC=B′C′.
在直角△ABC和直角△A′B′C′中,
,
∴△ABC≌△A′B′C′(SSS).
【总结升华】本题考查了直角三角形的全等中HL定理的证明,正确利用等腰三角形的性质是关键.
【巩固练习】
一、选择题
1.(2019春?深圳校级期中)下列语句中不正确的是( )
A.斜边和一锐角对应相等的两个直角三角形全等
B.有两边对应相等的两个直角三角形全等
C.有两个锐角相等的两个直角三角形全等
D.有一直角边和一锐角对应相等的两个直角三角形全等
2.如图,AB=AC,AD⊥ BC于D,E、F为AD上的点,则图中共有( )对全等三角形.
A.3 B.4 C.5 D.6
3. 能使两个直角三角形全等的条件是( )
A.斜边相等 B.一锐角对应相等
C.两锐角对应相等 D.两直角边对应相等
4. 在Rt△ABC与Rt△中, ∠C = ∠ = 90(, (A = ∠, AB =, 那么下列结论中正确的是( )
A. AC = B.BC = C. AC = D. ∠A = ∠
5. (2019春?蓝田县期末)如图,∠B=∠D=90°,BC=CD,∠1=40°,则∠2=( )
A.40° B.50° C.60° D.75°
6. 在两个直角三角形中,若有一对角对应相等,一对边对应相等,则两个直角三角形( )
A.一定全等 B.一定不全等 C.可能全等 D.以上都不是
二、填空题
7.如图,BE,CD是△ABC的高,且BD=EC,判定△BCD≌△CBE的依据是“______”.
8. 已知,如图,∠A=∠D=90°,BE=CF,AC=DE,则△ABC≌_______.
9. 如图,BA∥DC,∠A=90°,AB=CE,BC=ED,则AC=_________.
10.(2019春?普宁市期末)如图,已知AB⊥CD,垂足为B,BC=BE,若直接应用“HL”判定△ABC≌△DBE,则需要添加的一个条件是 .
11.有两个长度相同的滑梯,即BC=EF,左边滑梯的高度AC与右边滑梯的水平方向的长度DF相等,则∠ABC+∠DFE=________.
12. 如图,已知AD是△ABC的高,E为AC上一点,BE交AD于F,且BF=AC,FD=CD.则
∠BAD=_______.
三、解答题
13. 如图,工人师傅要在墙壁的O处用钻打孔,要使孔口从墙壁对面的B点处打开,墙壁厚是35,B点与O点的铅直距离AB长是20,工人师傅在旁边墙上与AO水平的线上截取OC=35,画CD⊥OC,使CD=20,连接OD,然后沿着DO的方向打孔,结果钻头正好从B点处打出,这是什么道理呢?请你说出理由.
14.(2019秋?黄石港区校级月考)如图,用三角尺可按下面方法画角平分线:在∠AOB的两边上分别取OM=ON,再分别过点M、N作OA、OB的垂线,交点为P,画射线OP,则得到OP平分∠AOB.请用你所学的知识说明其中的道理.
15. 如图,已知AB=AC,AE=AF,AE⊥EC,AF⊥BF,垂足分别是点E、F.
求证:∠1=∠2.
【答案与解析】
一、选择题
1. 【答案】C;
【解析】解:A、∵直角三角形的斜边和一锐角对应相等,所以另一锐角必然相等,∴符合ASA定理,故本选项正确;
B、两边对应相等的两个直角三角形全等,若是两条直角边,可以根据SAS判定全等,若是直角边与斜边,可根据HL判定全等.故本选项正确;
C、有两个锐角相等的两个直角三角形相似,故本选项错误;
D、有一直角边和一锐角对应相等的两个直角三角形符合ASA定理,可判定相等,故本选项正确.
故选C.
2. 【答案】D;
【解析】△ABD≌△ACD;△ABF≌△ACF;△ABE≌△ACE;△EBF≌△ECF;
△EBD≌△ECD;△FBD≌△FCD.
3. 【答案】D;
4. 【答案】C;
【解析】注意看清对应顶点,A对应,B对应.
5. 【答案】B;
【解析】解:∵∠B=∠D=90°,在Rt△ABC和Rt△ADC中
∴Rt△ABC≌Rt△ADC(HL)
∴∠2=∠ACB=90°﹣∠1=50°.
故选B.
6. 【答案】C;
【解析】如果这对角不是直角,那么全等,如果这对角是直角,那么不全等.
二、填空题
7. 【答案】HL;
8. 【答案】△DFE
9. 【答案】CD;
【解析】通过HL证Rt△ABC≌Rt△CDE.
10.【答案】AC=DE;
【解析】解∵AB⊥DC,
∴∠ABC=∠DBE=90°,
在Rt△ABC和Rt△DBE中,
,
∴Rt△ABC≌Rt△DBE(HL),
故答案为:AC=DE.
11.【答案】90°;
【解析】通过HL证Rt△ABC≌Rt△DEF,∠BCA=∠DFE.
12.【答案】45°;
【解析】证△ADC与△BDF全等,AD=BD,△ABD为等腰直角三角形.
三、解答题
13.【解析】
解:在Rt△AOB与Rt△COD中,
∴Rt△AOB≌Rt△COD(ASA)
∴AB=CD=20.
14.【解析】
解:在Rt△OPM和Rt△OPN中,
,
所以Rt△OPM≌Rt△OPN(HL),
所以∠POM=∠PON,
即OP平分∠AOB.
15.【解析】
证明:∵AE⊥EC,AF⊥BF,
∴△AEC、△AFB为直角三角形,
在Rt△AEC与Rt△AFB中,
∴Rt△AEC≌Rt△AFB(HL),
∴∠EAC=∠FAB,
∴∠EAC-∠BAC=∠FAB-∠BAC,即∠1=∠2.
【学习目标】
1.理解和掌握判定直角三角形全等的一种特殊方法——“斜边,直角边”(即“HL”).
2.能熟练地用判定一般三角形全等的方法及判定直角三角形的特殊方法判定两个直角三角形全等.
【要点梳理】
【 直角三角形全等的判定,知识点讲解】
要点一、判定直角三角形全等的一般方法
由三角形全等的条件可知,对于两个直角三角形,满足一边一锐角对应相等,或两直角边对应相等,这两个直角三角形就全等了.这里用到的是“AAS”,“ASA”或“SAS”判定定理.
要点二、判定直角三角形全等的特殊方法——斜边,直角边定理
在两个直角三角形中,有斜边和一条直角边对应相等的两个直角三角形全等(可以简写成“斜边、直角边”或“HL”).这个判定方法是直角三角形所独有的,一般三角形不具备.
要点诠释:(1)“HL”从顺序上讲是“边边角”对应相等,由于其中含有直角这个特殊条件,所以三角形的形状和大小就确定了.
(2)判定两个直角三角形全等的方法共有5种:SAS、ASA、AAS、SSS、HL.证明两个直角三角形全等,首先考虑用斜边、直角边定理,再考虑用一般三角形全等的证明方法.
(3)应用“斜边、直角边”判定两个直角三角形全等的过程中要突出直角三角形这个条件,书写时必须在两个三角形前加上“Rt”.
【典型例题】
类型一、直角三角形全等的判定——“HL”
1、 已知:如图,AB⊥BD,CD⊥BD,AD=BC.
求证:(1)AB=CD:
(2)AD∥BC.
【思路点拨】先由“HL”证Rt△ABD≌Rt△CDB,再由内错角相等证两直线平行.
【答案与解析】
证明:(1)∵AB⊥BD,CD⊥BD,
∴∠ABD=∠CDB=90°
在Rt△ABD 和Rt△CDB中,
∴Rt△ABD≌Rt△CDB(HL)
∴AB=CD(全等三角形对应边相等)
(2)由∠ADB=∠CBD
∴AD∥BC .
【总结升华】证明两个直角三角形全等,首先考虑用斜边、直角边定理,再考虑用一般三角形全等的证明方法.
举一反三:
【 直角三角形全等的判定,例3】
【变式】已知:如图,AE⊥AB,BC⊥AB,AE=AB,ED=AC.
求证:ED⊥AC.
【答案】
证明:∵AE⊥AB,BC⊥AB,
∴∠DAE=∠CBA=90°
在Rt△DAE 与Rt△CBA中,
∴Rt△DAE≌Rt△CBA (HL)
∴∠E=∠CAB
∵∠CAB+∠EAF=90°,
∴∠E+∠EAF=90°,即∠AFE=90°
即ED⊥AC.
2、 判断满足下列条件的两个直角三角形是否全等,不全等的画“×”,全等的注明理由:
(1)一个锐角和这个角的对边对应相等;( )
(2)一个锐角和斜边对应相等; ( )
(3)两直角边对应相等; ( )
(4)一条直角边和斜边对应相等. ( )
【答案】(1)全等,“AAS”;(2)全等,“AAS”;(3)全等,“SAS”;(4)全等,“HL”.
【解析】理解题意,画出图形,根据全等三角形的判定来判断.
【总结升华】直角三角形全等可用的判定方法有5种:SAS、ASA、AAS、SSS、HL.
举一反三:
【变式】下列说法正确的有( )
(1)一个锐角及斜边对应相等的两个直角三角形全等;
(2)一个锐角及一条直角边对应相等的两个直角三角形全等;
(3)两个锐角对应等的两个直角三角形全等;
(4)有两条边相等的两个直角三角形全等;
(5)有斜边和一条直角边对应相等的两个直角三角形全等.
A.2个 B.3个 C.4个 D.5个
【答案】C.
解:(1)一个锐角及斜边对应相等的两个直角三角形全等,根据AAS可判定两个直角三角形全等;(2)一个锐角及一条直角边对应相等的两个直角三角形全等,根据AAS或ASA可判定两个直角三角形全等;(3)两个锐角对应等的两个直角三角形全等,缺少“边”这个条件,故不可判定两个直角三角形全等;(4)有两条边相等的两个直角三角形全等,根据SAS或HL可判定两个直角三角形全等;(5)有斜边和一条直角边对应相等的两个直角三角形全等,根据HL可判定两个直角三角形全等.所以说法正确的有4个.故选C.
3、(2019春?深圳校级月考)如图,AB⊥AC于A,BD⊥CD于D,若AC=DB,则下列结论中不正确的是( )
A.∠A=∠D B.∠ABC=∠DCB C.OB=OD D.OA=OD
【思路点拨】根据已知及全等三角形的判定方法进行分析,从而得到答案.做题时要结合已知条件与全等的判定方法逐一验证.
【答案与解析】
解:∵AB⊥AC于A,BD⊥CD于D
∴∠A=∠D=90°(A正确)
又∵AC=DB,BC=BC
∴△ABC≌△DCB(HL)
∴∠ABC=∠DCB(B正确)
∴AB=CD
又∵∠AOB=∠C
∴△AOB≌△DOC(AAS)
∴OA=OD(D正确)
C中OD、OB不是对应边,不相等.
故选C.
【总结升华】本题考查三角形全等的判定方法,判定两个三角形全等的一般方法有:SSS、SAS、ASA、AAS、HL.注意:AAA、SSA不能判定两个三角形全等,判定两个三角形全等时,必须有边的参与,若有两边一角对应相等时,角必须是两边的夹角.
4、已知:如图1,在Rt△ABC和Rt△A′B′C′中,AB=A′B′,AC=A′C′,C=∠C′=90°
求证:Rt△ABC和Rt△A′B′C′全等.
(1)请你用“如果…,那么…”的形式叙述上述命题;
(2)将△ABC和△A′B′C′拼在一起,请你画出两种拼接图形;例如图2:(即使点A与点A′重合,点C与点C′重合.)
(3)请你选择你拼成的其中一种图形,证明该命题.
【答案与解析】
解:(1)如果一个直角三角形的斜边和一条直角边与另一个直角三角形的斜边和一条直角边分别相等,那么这两个直角三角形全等.
(2)如图:
图②使点A与点A′重合,点B与点B′重合
图③使点A与B′重合,B与点A′重合.
(3)在图②中,∵A和A′重合,B和B′重合,连接CC′.
∵∠ACB=∠A′C′B′=90°,∠ACB﹣∠ACC′=∠A′C′B′﹣∠AC′C,
即∠BCC′=∠BCC′,
∴BC=B′C′.
在直角△ABC和直角△A′B′C′中,
,
∴△ABC≌△A′B′C′(SSS).
【总结升华】本题考查了直角三角形的全等中HL定理的证明,正确利用等腰三角形的性质是关键.
【巩固练习】
一、选择题
1.(2019春?深圳校级期中)下列语句中不正确的是( )
A.斜边和一锐角对应相等的两个直角三角形全等
B.有两边对应相等的两个直角三角形全等
C.有两个锐角相等的两个直角三角形全等
D.有一直角边和一锐角对应相等的两个直角三角形全等
2.如图,AB=AC,AD⊥ BC于D,E、F为AD上的点,则图中共有( )对全等三角形.
A.3 B.4 C.5 D.6
3. 能使两个直角三角形全等的条件是( )
A.斜边相等 B.一锐角对应相等
C.两锐角对应相等 D.两直角边对应相等
4. 在Rt△ABC与Rt△中, ∠C = ∠ = 90(, (A = ∠, AB =, 那么下列结论中正确的是( )
A. AC = B.BC = C. AC = D. ∠A = ∠
5. (2019春?蓝田县期末)如图,∠B=∠D=90°,BC=CD,∠1=40°,则∠2=( )
A.40° B.50° C.60° D.75°
6. 在两个直角三角形中,若有一对角对应相等,一对边对应相等,则两个直角三角形( )
A.一定全等 B.一定不全等 C.可能全等 D.以上都不是
二、填空题
7.如图,BE,CD是△ABC的高,且BD=EC,判定△BCD≌△CBE的依据是“______”.
8. 已知,如图,∠A=∠D=90°,BE=CF,AC=DE,则△ABC≌_______.
9. 如图,BA∥DC,∠A=90°,AB=CE,BC=ED,则AC=_________.
10.(2019春?普宁市期末)如图,已知AB⊥CD,垂足为B,BC=BE,若直接应用“HL”判定△ABC≌△DBE,则需要添加的一个条件是 .
11.有两个长度相同的滑梯,即BC=EF,左边滑梯的高度AC与右边滑梯的水平方向的长度DF相等,则∠ABC+∠DFE=________.
12. 如图,已知AD是△ABC的高,E为AC上一点,BE交AD于F,且BF=AC,FD=CD.则
∠BAD=_______.
三、解答题
13. 如图,工人师傅要在墙壁的O处用钻打孔,要使孔口从墙壁对面的B点处打开,墙壁厚是35,B点与O点的铅直距离AB长是20,工人师傅在旁边墙上与AO水平的线上截取OC=35,画CD⊥OC,使CD=20,连接OD,然后沿着DO的方向打孔,结果钻头正好从B点处打出,这是什么道理呢?请你说出理由.
14.(2019秋?黄石港区校级月考)如图,用三角尺可按下面方法画角平分线:在∠AOB的两边上分别取OM=ON,再分别过点M、N作OA、OB的垂线,交点为P,画射线OP,则得到OP平分∠AOB.请用你所学的知识说明其中的道理.
15. 如图,已知AB=AC,AE=AF,AE⊥EC,AF⊥BF,垂足分别是点E、F.
求证:∠1=∠2.
【答案与解析】
一、选择题
1. 【答案】C;
【解析】解:A、∵直角三角形的斜边和一锐角对应相等,所以另一锐角必然相等,∴符合ASA定理,故本选项正确;
B、两边对应相等的两个直角三角形全等,若是两条直角边,可以根据SAS判定全等,若是直角边与斜边,可根据HL判定全等.故本选项正确;
C、有两个锐角相等的两个直角三角形相似,故本选项错误;
D、有一直角边和一锐角对应相等的两个直角三角形符合ASA定理,可判定相等,故本选项正确.
故选C.
2. 【答案】D;
【解析】△ABD≌△ACD;△ABF≌△ACF;△ABE≌△ACE;△EBF≌△ECF;
△EBD≌△ECD;△FBD≌△FCD.
3. 【答案】D;
4. 【答案】C;
【解析】注意看清对应顶点,A对应,B对应.
5. 【答案】B;
【解析】解:∵∠B=∠D=90°,在Rt△ABC和Rt△ADC中
∴Rt△ABC≌Rt△ADC(HL)
∴∠2=∠ACB=90°﹣∠1=50°.
故选B.
6. 【答案】C;
【解析】如果这对角不是直角,那么全等,如果这对角是直角,那么不全等.
二、填空题
7. 【答案】HL;
8. 【答案】△DFE
9. 【答案】CD;
【解析】通过HL证Rt△ABC≌Rt△CDE.
10.【答案】AC=DE;
【解析】解∵AB⊥DC,
∴∠ABC=∠DBE=90°,
在Rt△ABC和Rt△DBE中,
,
∴Rt△ABC≌Rt△DBE(HL),
故答案为:AC=DE.
11.【答案】90°;
【解析】通过HL证Rt△ABC≌Rt△DEF,∠BCA=∠DFE.
12.【答案】45°;
【解析】证△ADC与△BDF全等,AD=BD,△ABD为等腰直角三角形.
三、解答题
13.【解析】
解:在Rt△AOB与Rt△COD中,
∴Rt△AOB≌Rt△COD(ASA)
∴AB=CD=20.
14.【解析】
解:在Rt△OPM和Rt△OPN中,
,
所以Rt△OPM≌Rt△OPN(HL),
所以∠POM=∠PON,
即OP平分∠AOB.
15.【解析】
证明:∵AE⊥EC,AF⊥BF,
∴△AEC、△AFB为直角三角形,
在Rt△AEC与Rt△AFB中,
∴Rt△AEC≌Rt△AFB(HL),
∴∠EAC=∠FAB,
∴∠EAC-∠BAC=∠FAB-∠BAC,即∠1=∠2.
