5.3.2 命题、定理、证明 课件
图片预览






文档简介
(共20张PPT)
情境引入
有一天,歌德漫步在魏玛公园。不料,在一条小径遇到了一个曾把他的所有作品都贬得一文不值的批评家。这条狭窄的过道,只能通过一个人。他们面对面地相遇了。 那个批评家十分傲慢,他头一昂说:“对一个傻子,我绝不让路!”
“我却恰恰相反。”歌德微笑着,马上站到了一边。结果故作聪明的批评家,反倒自讨没趣。你知道为什么吗?
探究新知
(1)月季花是动物。
(2)直角是90°的角。
(3)对顶角相等。
(4)太阳从西边升起。
(5)若a2=b2,则a=b。
(不管判断是否正确)
定义:判断一件事情的语句,叫做命题。
下面的句子,有什么共同特征?
探究新知
下面哪些语句是命题,哪些不是。
(1)对顶角相等; ( )
(2)画一个角等于已知角; ( )
(3)两直线平行,内错角相等; ( )
(4)a、b两条直线垂直吗? ( )
(5)月季花是动物。 ( )
(6)啊,太漂亮了! ( )
(7)请你帮我倒杯茶。 ( )
不是
是
是
是
不是
不是
不是
探究新知
1.如果同位角相等,那么两直线平行。
2.如果两直线平行,那么内错角相等。
3.如果a∥b,b ∥c,那么a ∥c。
4.如果两个角不相等,那么这两个角不是对顶角。
观察下面的命题由几个部分组成。
探究新知
命题由 和 两部分组成。
命题的组成:
题设
结论
题设——是已知事项。
结论——是由已知事项推出的事项。
探究新知
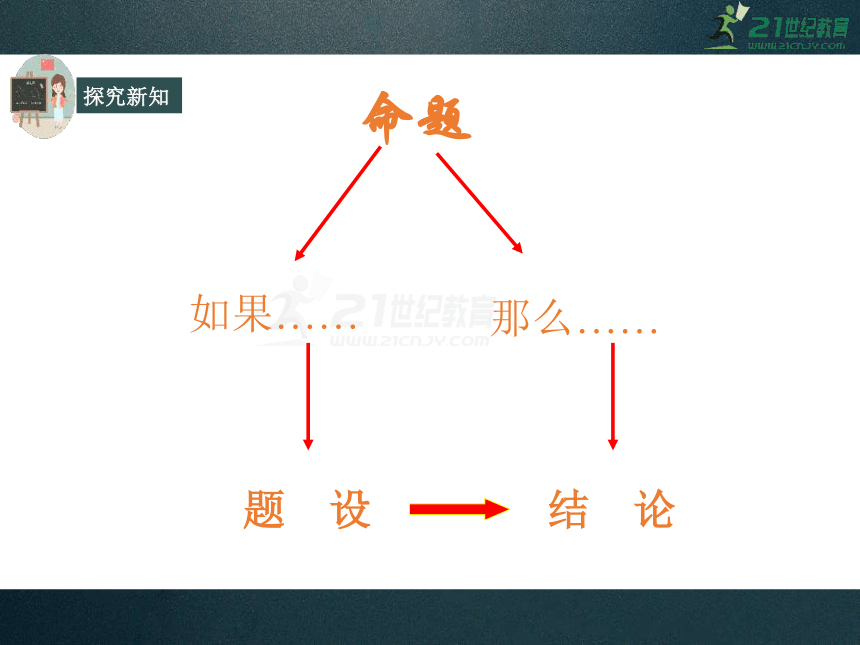
命题
如果……
那么……
题 设
结 论
做一做
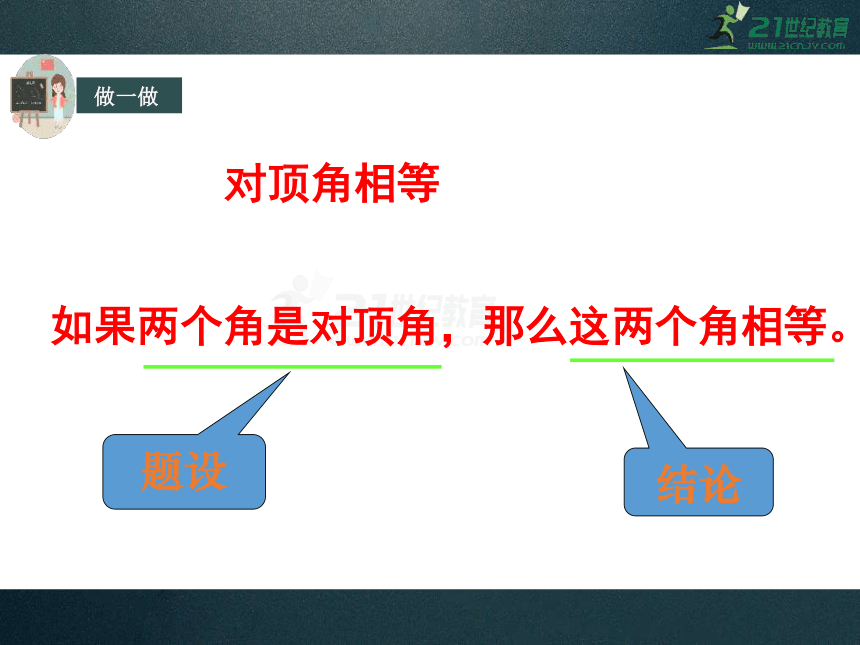
对顶角相等
结论
如果两个角是对顶角,那么这两个角相等。
题设
探究新知
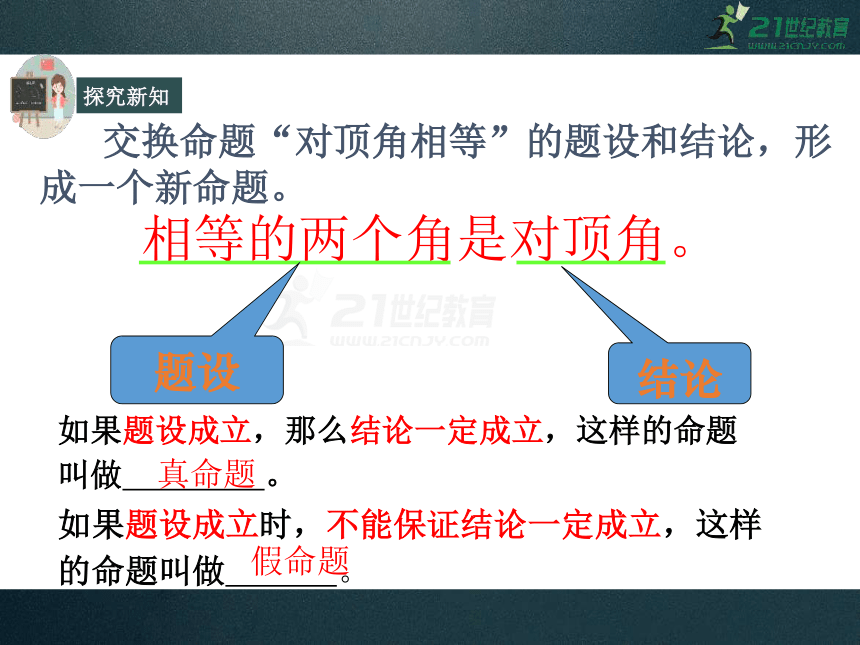
交换命题“对顶角相等”的题设和结论,形成一个新命题。
如果题设成立,那么结论一定成立,这样的命题
叫做 。
如果题设成立时,不能保证结论一定成立,这样
的命题叫做 。
真命题
假命题
相等的两个角是对顶角。
题设
结论
做一做
若a2 =b2,则a=b,这个命题是 命题。(填“真”或“假”)
注:判断一个命题是假命题时要举反例。
假
若a=b,则a2 =b2,这个命题是 命题。
真
探究新知
判断下列命题是真命题还是假命题。说明为什么是假命题。
(1)相等的角是对顶角; ( )
(2)两条平行线被第三条直线所截,同旁内角互补;( )
(3)经过直线外一点有且只有一条线段与已知直线平行。( )
(4)如果两个角的和为180°,那么这两个角互补;( )
(5)对顶角相等。( )
真命题
真命题
真命题
假命题
假命题
练一练
判断一个命题是假命题,也可举出一个例子
(反例),它符合命题的题设,但不满足结论就可以了.
举反例说明:“相等的角是对顶角”是假命题
解:如图所示,
OC是∠AOB的平分线
∴ ∠1=∠2
但∠1和∠2不是对顶角
∴“相等的角是对顶角”是假命题
探究新知
(1)在同一平面内,如果一条直线垂直于两条平行
线中的一条,那么也垂直于另一条;
(4)经过直线外一点有且只有一条直线与这条直线平行;
(5)两点确定一条直线.
上面命题正确性是经过推理证实的,这样得到的真命题叫做定理.
※定理也可以作为继续推理的依据.
探究新知
一个命题的正确性需要经过推理,才能作出判断,这个推理过程叫做 。证明的每一步都要有依据。
证明
“在同一平面内,如果一条直线垂直于两条平行线中的一条,那么它也垂直于另一条。”你能根据命题画图,用几何语言表述命题的题设和结论吗?
这是一个真命题,你说一说理由吗?
练一练
已知:如图,直线b∥c, a⊥c. 求证:a⊥b
∵a⊥c
∴∠1=90°
又b∥c
(两直线平行,同位角相等).
∴a⊥b
证明:
( 已知)
(垂直的定义)
( 已知)
∴∠1=∠2
∴∠2=∠1=90°
(等量代换).
(垂直的定义).
随堂训练
1.下列语句属于命题的是( )
A.B是什么数? B. 延长AB到C,使BC=AB
C. 对顶角不相等 D. 连结A、C两点
2.下列说法:
①在同一平面内不相交的两条线段必平行;
②在同一平面内不相交的两条直线必平行;
③在同一平面内垂直于同一条直线的两条直线互相垂直;
④在同一平面内平行于同一条直线的两条直线互相平行。
假命题有( )
A.4个 B.2个 C.3个 D.1个
C
B
随堂训练
3.如图DE∥BC,∠1=∠3,CD⊥AB,证明FG⊥AB。
∵DE∥BC
∴∠1=∠2
又∵∠1=∠3
∴FG⊥AB
证明:
∴∠2=∠3
∴FG∥CD
又∵CD⊥AB
拓展延伸
如图FG⊥AB,∠1=∠3,CD⊥AB,请证明为什么DE∥BC?
∴FG∥CD
∴∠2=∠3
∵CD⊥AB FG⊥AB
证明:
∵∠1=∠3
∴∠1=∠2
∴DE∥BC
课堂小结
1.命题:判断一件事情的语句叫命题。
(1)命题的结构:命题由题设和结论两部分构成,常可写成“如果…,那么…”的形式。
(2)如果题设成立,那么结论一定成立,这样的命题叫做真命题,如果题设成立时,不能保证结论一定成立,这样的命题叫做假命题。
(3)判断一个命题是假命题,只要举出一个例子,说明该命题不成立就可以了,这种方法称为举反例。
2.定理:经过推理论证为正确的命题叫定理。也可作为继续推理的依据(定理都是真命题) 。
3.判断一个命题是真命题,可以从定理出发,用逻辑推理的方法证明。
https://www.21cnjy.com/help/help_extract.php
情境引入
有一天,歌德漫步在魏玛公园。不料,在一条小径遇到了一个曾把他的所有作品都贬得一文不值的批评家。这条狭窄的过道,只能通过一个人。他们面对面地相遇了。 那个批评家十分傲慢,他头一昂说:“对一个傻子,我绝不让路!”
“我却恰恰相反。”歌德微笑着,马上站到了一边。结果故作聪明的批评家,反倒自讨没趣。你知道为什么吗?
探究新知
(1)月季花是动物。
(2)直角是90°的角。
(3)对顶角相等。
(4)太阳从西边升起。
(5)若a2=b2,则a=b。
(不管判断是否正确)
定义:判断一件事情的语句,叫做命题。
下面的句子,有什么共同特征?
探究新知
下面哪些语句是命题,哪些不是。
(1)对顶角相等; ( )
(2)画一个角等于已知角; ( )
(3)两直线平行,内错角相等; ( )
(4)a、b两条直线垂直吗? ( )
(5)月季花是动物。 ( )
(6)啊,太漂亮了! ( )
(7)请你帮我倒杯茶。 ( )
不是
是
是
是
不是
不是
不是
探究新知
1.如果同位角相等,那么两直线平行。
2.如果两直线平行,那么内错角相等。
3.如果a∥b,b ∥c,那么a ∥c。
4.如果两个角不相等,那么这两个角不是对顶角。
观察下面的命题由几个部分组成。
探究新知
命题由 和 两部分组成。
命题的组成:
题设
结论
题设——是已知事项。
结论——是由已知事项推出的事项。
探究新知
命题
如果……
那么……
题 设
结 论
做一做
对顶角相等
结论
如果两个角是对顶角,那么这两个角相等。
题设
探究新知
交换命题“对顶角相等”的题设和结论,形成一个新命题。
如果题设成立,那么结论一定成立,这样的命题
叫做 。
如果题设成立时,不能保证结论一定成立,这样
的命题叫做 。
真命题
假命题
相等的两个角是对顶角。
题设
结论
做一做
若a2 =b2,则a=b,这个命题是 命题。(填“真”或“假”)
注:判断一个命题是假命题时要举反例。
假
若a=b,则a2 =b2,这个命题是 命题。
真
探究新知
判断下列命题是真命题还是假命题。说明为什么是假命题。
(1)相等的角是对顶角; ( )
(2)两条平行线被第三条直线所截,同旁内角互补;( )
(3)经过直线外一点有且只有一条线段与已知直线平行。( )
(4)如果两个角的和为180°,那么这两个角互补;( )
(5)对顶角相等。( )
真命题
真命题
真命题
假命题
假命题
练一练
判断一个命题是假命题,也可举出一个例子
(反例),它符合命题的题设,但不满足结论就可以了.
举反例说明:“相等的角是对顶角”是假命题
解:如图所示,
OC是∠AOB的平分线
∴ ∠1=∠2
但∠1和∠2不是对顶角
∴“相等的角是对顶角”是假命题
探究新知
(1)在同一平面内,如果一条直线垂直于两条平行
线中的一条,那么也垂直于另一条;
(4)经过直线外一点有且只有一条直线与这条直线平行;
(5)两点确定一条直线.
上面命题正确性是经过推理证实的,这样得到的真命题叫做定理.
※定理也可以作为继续推理的依据.
探究新知
一个命题的正确性需要经过推理,才能作出判断,这个推理过程叫做 。证明的每一步都要有依据。
证明
“在同一平面内,如果一条直线垂直于两条平行线中的一条,那么它也垂直于另一条。”你能根据命题画图,用几何语言表述命题的题设和结论吗?
这是一个真命题,你说一说理由吗?
练一练
已知:如图,直线b∥c, a⊥c. 求证:a⊥b
∵a⊥c
∴∠1=90°
又b∥c
(两直线平行,同位角相等).
∴a⊥b
证明:
( 已知)
(垂直的定义)
( 已知)
∴∠1=∠2
∴∠2=∠1=90°
(等量代换).
(垂直的定义).
随堂训练
1.下列语句属于命题的是( )
A.B是什么数? B. 延长AB到C,使BC=AB
C. 对顶角不相等 D. 连结A、C两点
2.下列说法:
①在同一平面内不相交的两条线段必平行;
②在同一平面内不相交的两条直线必平行;
③在同一平面内垂直于同一条直线的两条直线互相垂直;
④在同一平面内平行于同一条直线的两条直线互相平行。
假命题有( )
A.4个 B.2个 C.3个 D.1个
C
B
随堂训练
3.如图DE∥BC,∠1=∠3,CD⊥AB,证明FG⊥AB。
∵DE∥BC
∴∠1=∠2
又∵∠1=∠3
∴FG⊥AB
证明:
∴∠2=∠3
∴FG∥CD
又∵CD⊥AB
拓展延伸
如图FG⊥AB,∠1=∠3,CD⊥AB,请证明为什么DE∥BC?
∴FG∥CD
∴∠2=∠3
∵CD⊥AB FG⊥AB
证明:
∵∠1=∠3
∴∠1=∠2
∴DE∥BC
课堂小结
1.命题:判断一件事情的语句叫命题。
(1)命题的结构:命题由题设和结论两部分构成,常可写成“如果…,那么…”的形式。
(2)如果题设成立,那么结论一定成立,这样的命题叫做真命题,如果题设成立时,不能保证结论一定成立,这样的命题叫做假命题。
(3)判断一个命题是假命题,只要举出一个例子,说明该命题不成立就可以了,这种方法称为举反例。
2.定理:经过推理论证为正确的命题叫定理。也可作为继续推理的依据(定理都是真命题) 。
3.判断一个命题是真命题,可以从定理出发,用逻辑推理的方法证明。
https://www.21cnjy.com/help/help_extract.php
