人教新课标A版数学必修2 2.2 直线与平面平行、平面与平面平行的判定(共21张ppt)
文档属性
| 名称 | 人教新课标A版数学必修2 2.2 直线与平面平行、平面与平面平行的判定(共21张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.6MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-06 10:56:19 | ||
图片预览





文档简介
课件21张PPT。直线与平面平面与平面平行的判定(一)教学目标
1.知识与技能
(1)?通过直观感知、操作确认,理解并掌握直线与平面平行、平面与平面平行的判定定理;
(2)进一步培养学生观察、发现的能力和空间想象能力;
2.过程与方法
学生通过观察图形,借助已有知识,掌握直线与平面平行、 平面与平面平行的判定定理.
3.情感、态度与价值观
(1)让学生亲身经历数学研究的过程,体验创造的激情,享受成功的喜悦,感受数学的魅力。 (2)让学生了解空间与平面互相转换的数学思想.
(二)教学重点、难点
重点、难点:通过直观感知、操作确认,归纳出线与面,面与面平行的判定及其应用。 直线EF与椅子面α是
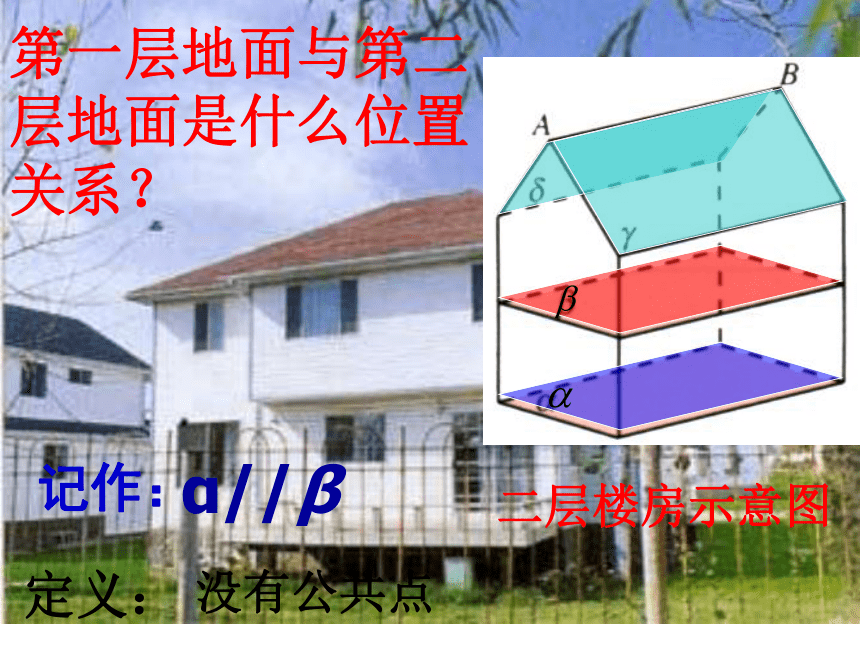
什么位置关系呢?椅子示意图EF∥α没有公共点定义: 记作:二层楼房示意图第一层地面与第二层地面是什么位置关系?α//β没有公共点定义: 记作:观察:根据定义,判定线与面是否平行,只需判定线与面是否有公共点。但是,直线无限延长,平面无限延展,有没有公共点是看不出来的,那么如何判定平行呢?l与平面α
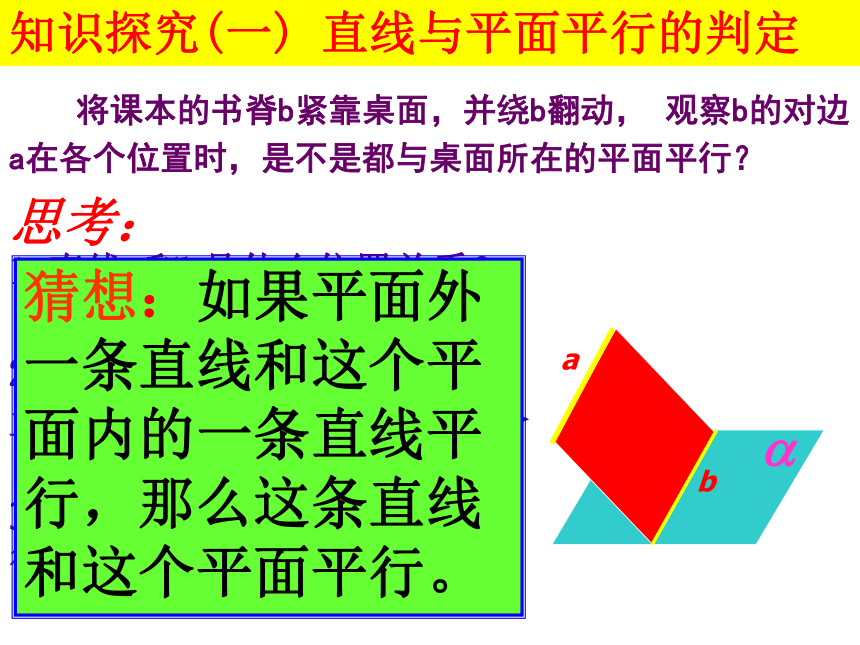
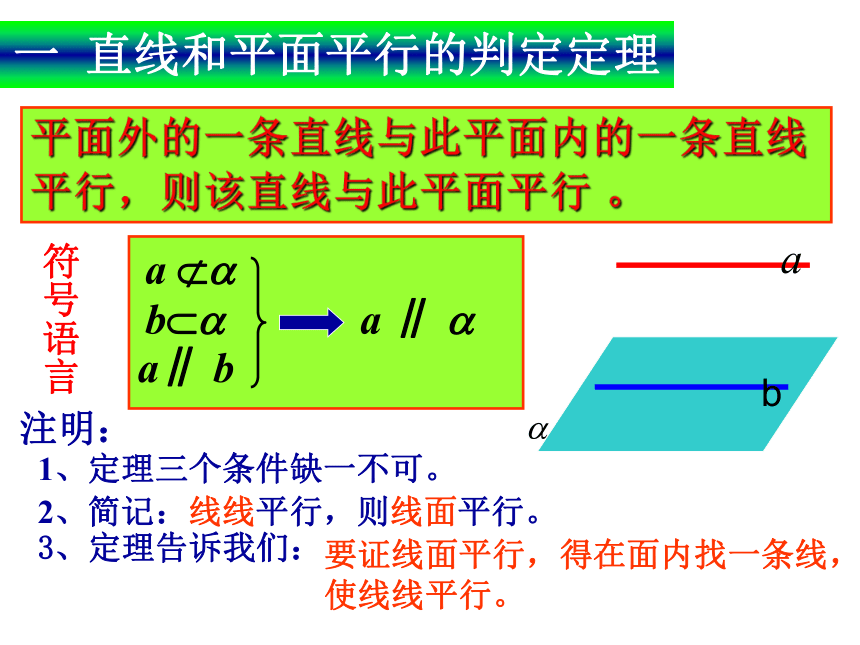
平行吗? 将课本的书脊b紧靠桌面,并绕b翻动, 观察b的对边a在各个位置时,是不是都与桌面所在的平面平行?转化平面知识探究(一) 直线与平面平行的判定 abab1 直线a和b是什么位置关系?2 a与b所在平面?什么位置关系?3 由上你能猜想出判定线面平行的关键所在吗?思考:猜想:如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行。?证明:假设直线a不平行于平面α,则a ∩ α= P一 直线和平面平行的判定定理平面外的一条直线与此平面内的一条直线平行,则该直线与此平面平行 。b??a∥ ba ??a ∥ ?注明:1、定理三个条件缺一不可。2、简记:线线平行,则线面平行。3、定理告诉我们:要证线面平行,得在面内找一条线,使线线平行。b符号语言 空间四边形ABCD中,E,F,分别是AB,DA的中点。
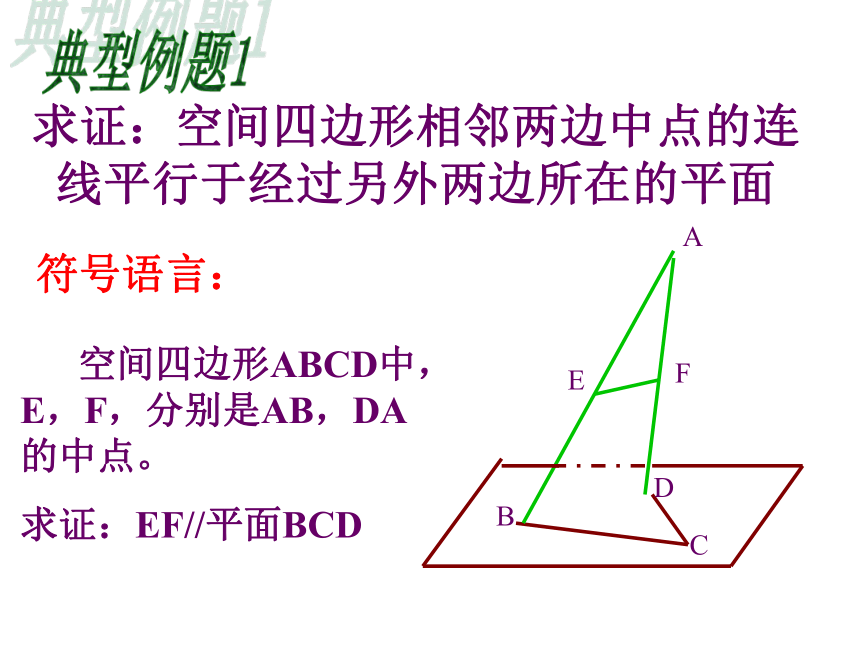
求证:EF//平面BCD典型例题1求证:空间四边形相邻两边中点的连线平行于经过另外两边所在的平面符号语言:证明:连结BD EF ∥BDEF ? 平面BDCBD ? 平面BDCEF∥平面BCD.因为E,F为中点 快速作答练习1:如图,长方体 中,
①与 平行的平面是 ____________________________
②与 平行的平面是____________________________
③与 平行的平面是________________________快速作答牛刀小试练习2 正方体ABCD-A1B1C1D1中,
求证 (1) AD1 // 平面BDC1 (2) D1B1 // 平面BDC1平面AD1B1与平面DBC1是什么位置关系呢?探究 给定下列条件:
①两个平面不相交
②两个平面没有公共点
③一个平面内所有直线都平行于另一个平面
④一个平面内有一条直线平行于另一个平面
⑤一个平面内有两条直线平行于另一个平面
以上条件能判断两个平面平行的有_______①②③知识探究(二)平面与平面平行的判定(两平面相交) (两平面平行)命题错误 × ④若 内有一条直线 与平面 平行,则 与 平行(两平面平行)(两平面相交) (两平面平行)a // ba∩b=P两 种 情 况唯 一⑤若 内有两条直线 , 与平面 平行,则 与 平行命题错误命题正确 判定定理:一个平面内两条相交直线与另一个平面平行,则这两个平面平行.P符号
语言:二 平面和平面平行的判定定理判定定理剖析:直线证题思路:要证明两平面平行,关键是在其中一个平面内找出两条相交直线分别平行于另一个平面.
练4.判断下列命题是否正确,正确的说明理由,错误的举例说明:
(1)已知平面α , β和直线m,n,若m ? α,n ? α,m// β,n// β则α // β ;
(2)一个平面α内两条不平行直线都平行于另一平面β ,则α // β ;正确错误练5.平面α与平面β平行的条件可以是( )
(A)α内有无穷多条直线都与β平行.
(B)直线a∥α ,a∥β ,且直 线a不在α内,也不在β内.
(C)直线 a ? α,直线b ? β, 且 a// β,b// α
(D)α内的任何直线都与β平行. D书接上回:经典例2
证明:1.证明直线与平面平行、平面与平面平行的方法:(1)利用定义:没有公共点。(2)利用判定定理.2.数学思想方法:转化的思想知识小结:小测:
如图,正方体ABCD – A1B1C1D1 中,M,N,E,F分别是棱A1B1,A1D1,B1C1,C1D1的中点.
求证:
平面AMN∥平面EFDB.
1.知识与技能
(1)?通过直观感知、操作确认,理解并掌握直线与平面平行、平面与平面平行的判定定理;
(2)进一步培养学生观察、发现的能力和空间想象能力;
2.过程与方法
学生通过观察图形,借助已有知识,掌握直线与平面平行、 平面与平面平行的判定定理.
3.情感、态度与价值观
(1)让学生亲身经历数学研究的过程,体验创造的激情,享受成功的喜悦,感受数学的魅力。 (2)让学生了解空间与平面互相转换的数学思想.
(二)教学重点、难点
重点、难点:通过直观感知、操作确认,归纳出线与面,面与面平行的判定及其应用。 直线EF与椅子面α是
什么位置关系呢?椅子示意图EF∥α没有公共点定义: 记作:二层楼房示意图第一层地面与第二层地面是什么位置关系?α//β没有公共点定义: 记作:观察:根据定义,判定线与面是否平行,只需判定线与面是否有公共点。但是,直线无限延长,平面无限延展,有没有公共点是看不出来的,那么如何判定平行呢?l与平面α
平行吗? 将课本的书脊b紧靠桌面,并绕b翻动, 观察b的对边a在各个位置时,是不是都与桌面所在的平面平行?转化平面知识探究(一) 直线与平面平行的判定 abab1 直线a和b是什么位置关系?2 a与b所在平面?什么位置关系?3 由上你能猜想出判定线面平行的关键所在吗?思考:猜想:如果平面外一条直线和这个平面内的一条直线平行,那么这条直线和这个平面平行。?证明:假设直线a不平行于平面α,则a ∩ α= P一 直线和平面平行的判定定理平面外的一条直线与此平面内的一条直线平行,则该直线与此平面平行 。b??a∥ ba ??a ∥ ?注明:1、定理三个条件缺一不可。2、简记:线线平行,则线面平行。3、定理告诉我们:要证线面平行,得在面内找一条线,使线线平行。b符号语言 空间四边形ABCD中,E,F,分别是AB,DA的中点。
求证:EF//平面BCD典型例题1求证:空间四边形相邻两边中点的连线平行于经过另外两边所在的平面符号语言:证明:连结BD EF ∥BDEF ? 平面BDCBD ? 平面BDCEF∥平面BCD.因为E,F为中点 快速作答练习1:如图,长方体 中,
①与 平行的平面是 ____________________________
②与 平行的平面是____________________________
③与 平行的平面是________________________快速作答牛刀小试练习2 正方体ABCD-A1B1C1D1中,
求证 (1) AD1 // 平面BDC1 (2) D1B1 // 平面BDC1平面AD1B1与平面DBC1是什么位置关系呢?探究 给定下列条件:
①两个平面不相交
②两个平面没有公共点
③一个平面内所有直线都平行于另一个平面
④一个平面内有一条直线平行于另一个平面
⑤一个平面内有两条直线平行于另一个平面
以上条件能判断两个平面平行的有_______①②③知识探究(二)平面与平面平行的判定(两平面相交) (两平面平行)命题错误 × ④若 内有一条直线 与平面 平行,则 与 平行(两平面平行)(两平面相交) (两平面平行)a // ba∩b=P两 种 情 况唯 一⑤若 内有两条直线 , 与平面 平行,则 与 平行命题错误命题正确 判定定理:一个平面内两条相交直线与另一个平面平行,则这两个平面平行.P符号
语言:二 平面和平面平行的判定定理判定定理剖析:直线证题思路:要证明两平面平行,关键是在其中一个平面内找出两条相交直线分别平行于另一个平面.
练4.判断下列命题是否正确,正确的说明理由,错误的举例说明:
(1)已知平面α , β和直线m,n,若m ? α,n ? α,m// β,n// β则α // β ;
(2)一个平面α内两条不平行直线都平行于另一平面β ,则α // β ;正确错误练5.平面α与平面β平行的条件可以是( )
(A)α内有无穷多条直线都与β平行.
(B)直线a∥α ,a∥β ,且直 线a不在α内,也不在β内.
(C)直线 a ? α,直线b ? β, 且 a// β,b// α
(D)α内的任何直线都与β平行. D书接上回:经典例2
证明:1.证明直线与平面平行、平面与平面平行的方法:(1)利用定义:没有公共点。(2)利用判定定理.2.数学思想方法:转化的思想知识小结:小测:
如图,正方体ABCD – A1B1C1D1 中,M,N,E,F分别是棱A1B1,A1D1,B1C1,C1D1的中点.
求证:
平面AMN∥平面EFDB.
