人教新课标A版数学必修2 2.1.1 平面(共16张ppt)
文档属性
| 名称 | 人教新课标A版数学必修2 2.1.1 平面(共16张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 770.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-06 11:03:29 | ||
图片预览



文档简介
课件16张PPT。2.1.1 平面观察生活实例(类比直线)引入平面观察教室里的桌面、黑板面,给我们怎样的直观感觉?生活中还有那些物体呈现这样的形象?是无限延展的
几何中的平面就是从这些物体中抽象出来的,是平的、光滑的、无大小、无厚度,
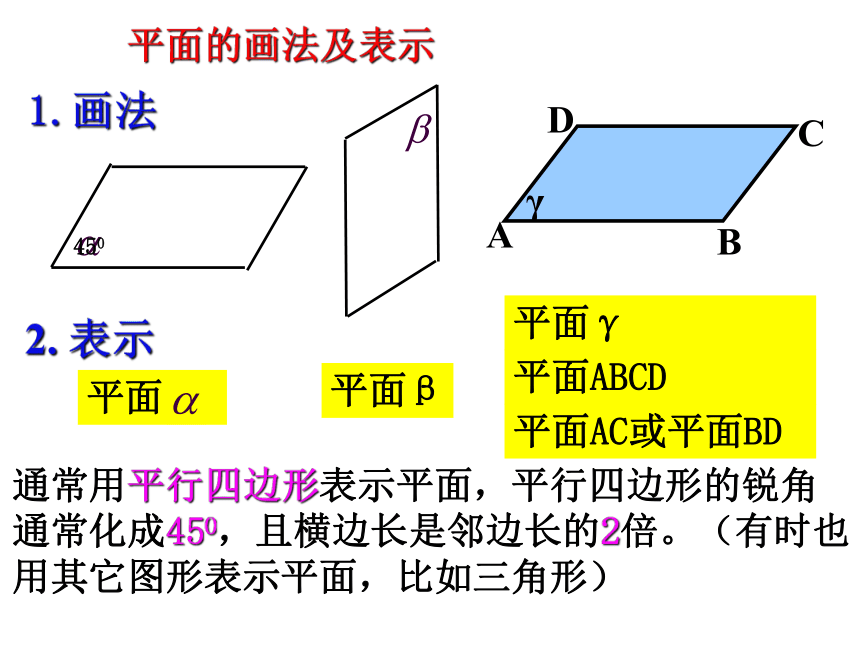
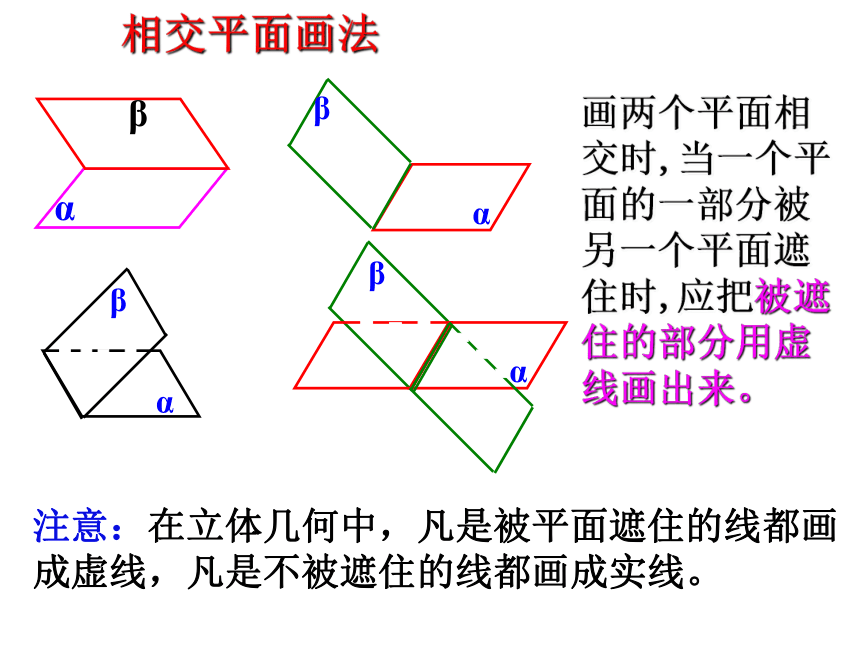
1.画法ABCD通常用平行四边形表示平面,平行四边形的锐角通常化成450,且横边长是邻边长的2倍。(有时也用其它图形表示平面,比如三角形)平面AC或平面BD平面ABCDγ平面平面β平面γ2. 表示平面的画法及表示450相交平面画法β画两个平面相交时,当一个平面的一部分被另一个平面遮住时,应把被遮住的部分用虚线画出来。注意:在立体几何中,凡是被平面遮住的线都画成虚线,凡是不被遮住的线都画成实线。类比集合空间中点、线、面的位置关系 图形语言 文字语言 符号语言lA点A在直线 上
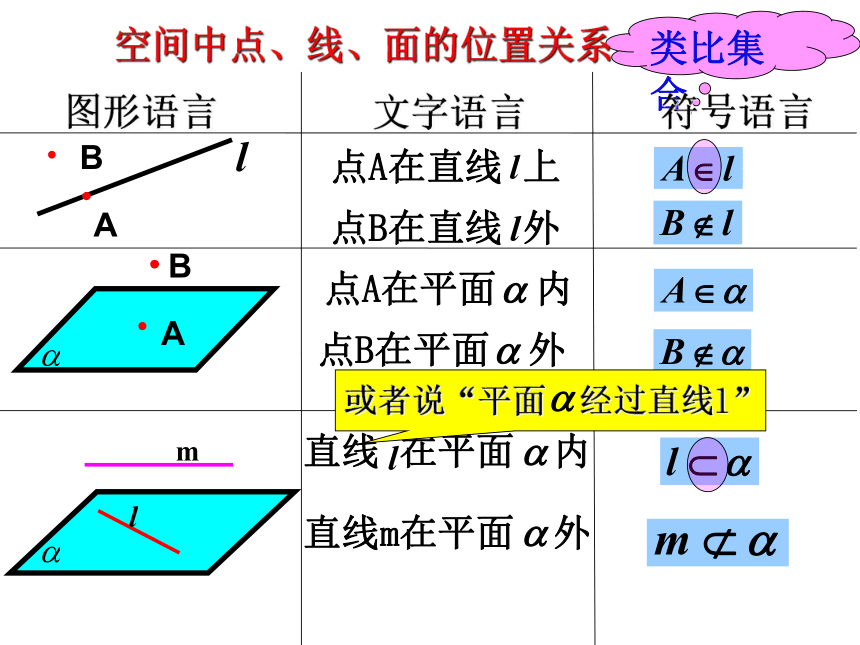
B点B在直线 外
AB点A在平面 内点B在平面 外 直线 在平面 内直线m在平面 外线与面的关系(分组讨论)请你用笔和纸板做实验并回答以下问题
1、如果一直线与一平面有一个公共点,那么这条直线在平面内吗?
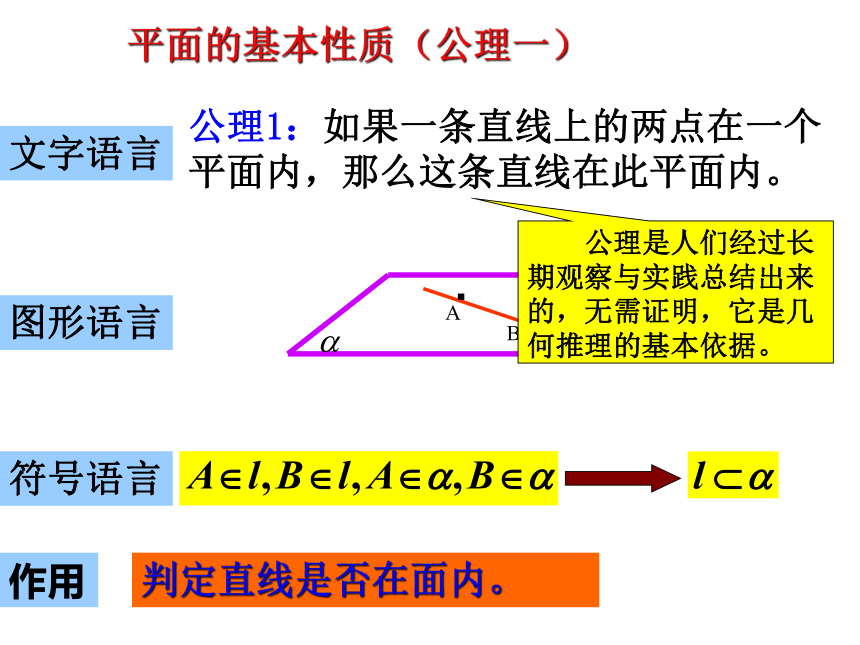
2、如果一直线与一平面有两个公共点,那么这条直线在平面内吗?在不在文字语言图形语言符号语言B··A·..公理1:如果一条直线上的两点在一个平面内,那么这条直线在此平面内。判定直线是否在面内。平面的基本性质(公理一)作用 公理是人们经过长期观察与实践总结出来的,无需证明,它是几何推理的基本依据。请你用纸板做实验并回答以下问题:
1、过一点有几个平面?2、过两点有几个平面?
3、过在同一直线上的三点有几个平面?
4、过不在同一直线上的三点有几个平面?点与面关系(分组讨论)确定一个平面的依据.记作:平面ABC 公理2:过不在一条直线上的三点,存在性唯一性平面的基本性质(公理二)文字语言图形语言符号语言作用有且只有一个平面.——可以——可以——可以1.直线和直线外一点可以确定一个平面吗?2.两条相交直线可以确定一个平面吗?3.两条平行直线可以确定一个平面吗?点线面的关系(分组讨论)推论1:过直线和直线外一点有且只有一个平面。推论2:过两条相交直线有且只有一个平面。推论3:过两条平行直线有且只有一个平面。两两相交且不共点的三条直线确定一个平面吗? 把三角板的一个角立在课桌面上,三角板所在平面与桌面所在平面是否只相交于一点B?为什么?B面与面的关系(分组讨论)否,因为平面是无限延展的,应交于一条线。公理3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.①判断两个平面相交的依据②判断点在直线上平面的基本性质(公理三)文字语言图形语言作用符号语言类比集合(即这样的公共点有无限个且都在一条直线上)例1 用符号表示下列图形中点、直线、平面之间的位置关系.(1)解:(1)典型例题课堂练习 2、在空间中,可以确定一个平面的是( )1、下列关于平面的说法正确的是( )A.一个平面长 4 米,宽 2 米;B.平面有边界;C.一个平面的面积是 25 cm ;D.经过一条直线和一个点
A.两两相交的三条直线 B.三个点 C.两两相交且不共点的三条直线D.菱形的面积是 4cm ; DC3.判断下列各题的说法正确与否?
(1)一个平面可以把空间分成两部分 ( )
(2)四边形确定一个平面( )
(3) 经过两条平行直线可以确定一个平面( )
(4)如果两个平面有三个不共线的公共点,那么这两个平面重合。 ( )
×√ √分为平面四边形(包括梯形,平行四边形等)和空间四边形
课堂练习 √本节小结: 一.平面的特征;三.空间中点、直线、平面间位置关系的
文字语言,图形语言和符号语言之间
的转化;二.平面的画法及表示;四.三条公理与三条推论.
1.画法ABCD通常用平行四边形表示平面,平行四边形的锐角通常化成450,且横边长是邻边长的2倍。(有时也用其它图形表示平面,比如三角形)平面AC或平面BD平面ABCDγ平面平面β平面γ2. 表示平面的画法及表示450相交平面画法β画两个平面相交时,当一个平面的一部分被另一个平面遮住时,应把被遮住的部分用虚线画出来。注意:在立体几何中,凡是被平面遮住的线都画成虚线,凡是不被遮住的线都画成实线。类比集合空间中点、线、面的位置关系 图形语言 文字语言 符号语言lA点A在直线 上
B点B在直线 外
AB点A在平面 内点B在平面 外 直线 在平面 内直线m在平面 外线与面的关系(分组讨论)请你用笔和纸板做实验并回答以下问题
1、如果一直线与一平面有一个公共点,那么这条直线在平面内吗?
2、如果一直线与一平面有两个公共点,那么这条直线在平面内吗?在不在文字语言图形语言符号语言B··A·..公理1:如果一条直线上的两点在一个平面内,那么这条直线在此平面内。判定直线是否在面内。平面的基本性质(公理一)作用 公理是人们经过长期观察与实践总结出来的,无需证明,它是几何推理的基本依据。请你用纸板做实验并回答以下问题:
1、过一点有几个平面?2、过两点有几个平面?
3、过在同一直线上的三点有几个平面?
4、过不在同一直线上的三点有几个平面?点与面关系(分组讨论)确定一个平面的依据.记作:平面ABC 公理2:过不在一条直线上的三点,存在性唯一性平面的基本性质(公理二)文字语言图形语言符号语言作用有且只有一个平面.——可以——可以——可以1.直线和直线外一点可以确定一个平面吗?2.两条相交直线可以确定一个平面吗?3.两条平行直线可以确定一个平面吗?点线面的关系(分组讨论)推论1:过直线和直线外一点有且只有一个平面。推论2:过两条相交直线有且只有一个平面。推论3:过两条平行直线有且只有一个平面。两两相交且不共点的三条直线确定一个平面吗? 把三角板的一个角立在课桌面上,三角板所在平面与桌面所在平面是否只相交于一点B?为什么?B面与面的关系(分组讨论)否,因为平面是无限延展的,应交于一条线。公理3:如果两个不重合的平面有一个公共点,那么它们有且只有一条过该点的公共直线.①判断两个平面相交的依据②判断点在直线上平面的基本性质(公理三)文字语言图形语言作用符号语言类比集合(即这样的公共点有无限个且都在一条直线上)例1 用符号表示下列图形中点、直线、平面之间的位置关系.(1)解:(1)典型例题课堂练习 2、在空间中,可以确定一个平面的是( )1、下列关于平面的说法正确的是( )A.一个平面长 4 米,宽 2 米;B.平面有边界;C.一个平面的面积是 25 cm ;D.经过一条直线和一个点
A.两两相交的三条直线 B.三个点 C.两两相交且不共点的三条直线D.菱形的面积是 4cm ; DC3.判断下列各题的说法正确与否?
(1)一个平面可以把空间分成两部分 ( )
(2)四边形确定一个平面( )
(3) 经过两条平行直线可以确定一个平面( )
(4)如果两个平面有三个不共线的公共点,那么这两个平面重合。 ( )
×√ √分为平面四边形(包括梯形,平行四边形等)和空间四边形
课堂练习 √本节小结: 一.平面的特征;三.空间中点、直线、平面间位置关系的
文字语言,图形语言和符号语言之间
的转化;二.平面的画法及表示;四.三条公理与三条推论.
