人教版数学必修2 2.1.2 空间中直线与直线之间的位置关系(共30张ppt)
文档属性
| 名称 | 人教版数学必修2 2.1.2 空间中直线与直线之间的位置关系(共30张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 405.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-06 19:02:08 | ||
图片预览



文档简介
课件20张PPT。2.1.2 空间中直线与
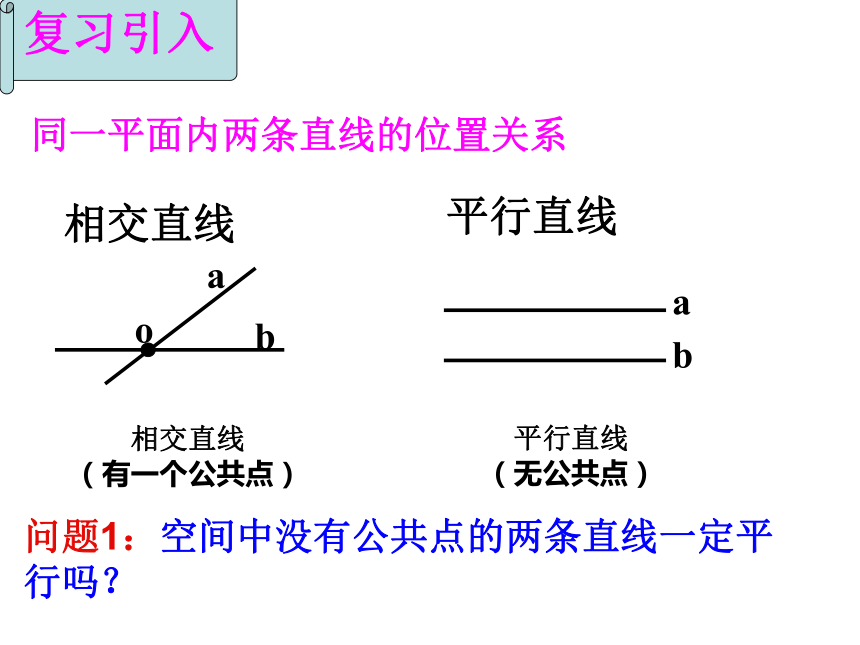
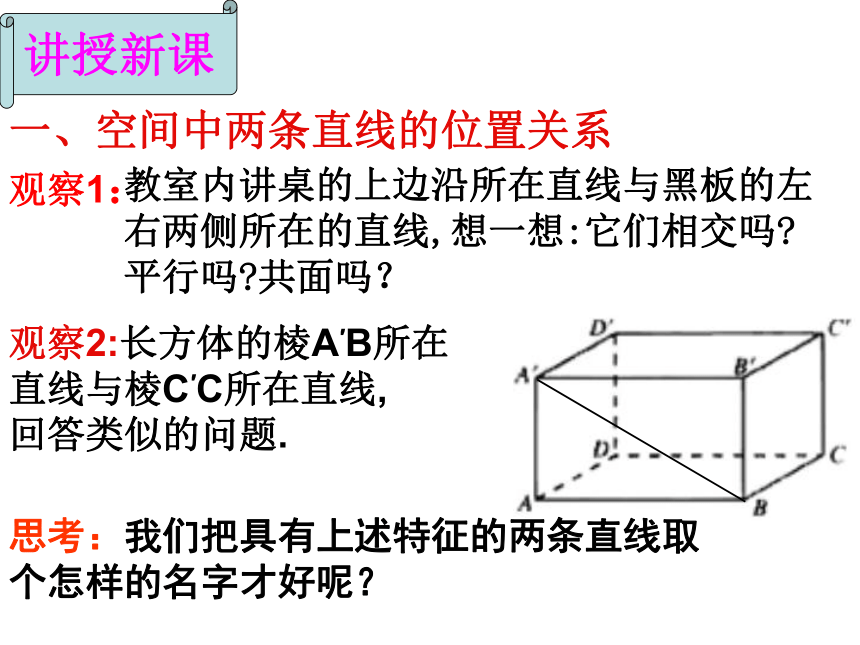
直线之间的位置关系学习目标知识与技能:会判断空间两直线的位置关系,理解公理四,掌握异面直线的概念及所成的角。过程与方法:用实例引出异面直线的概念,介绍空间直线位置关系,进而由公理4引出异面直线所成的角。学习重点:空间两直线的位置关系及异面直线所成的角。学习难点:求异面直线所成的角。学习方法:类比式、探索启发式情感态度价值观:培养学生观察,发现,总结以及动手操作的能力,增强空间立体感。同一平面内两条直线的位置关系复习引入问题1:空间中没有公共点的两条直线一定平行吗?观察1:教室内讲桌的上边沿所在直线与黑板的左右两侧所在的直线,想一想:它们相交吗?平行吗?共面吗?观察2:长方体的棱A′B所在
直线与棱C′C所在直线,
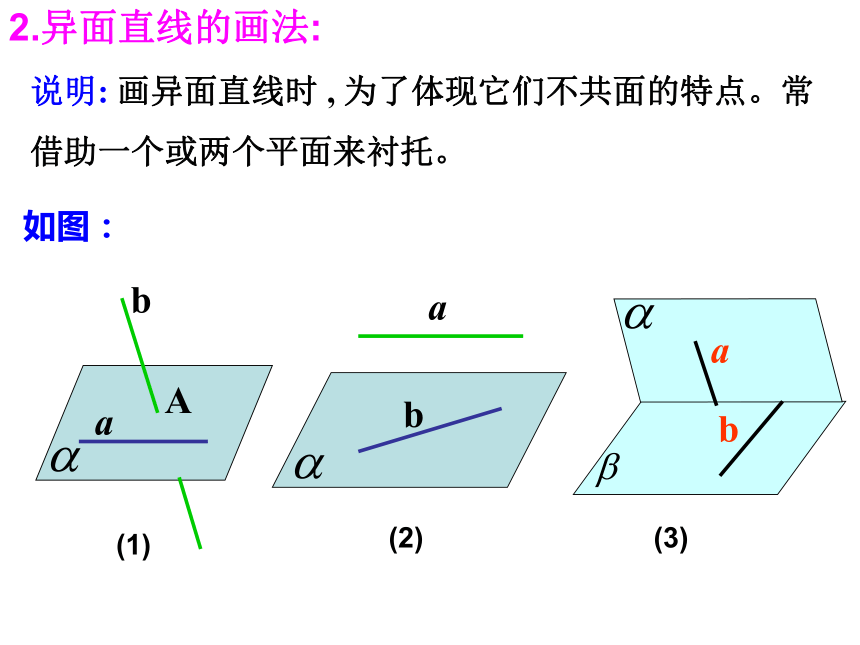
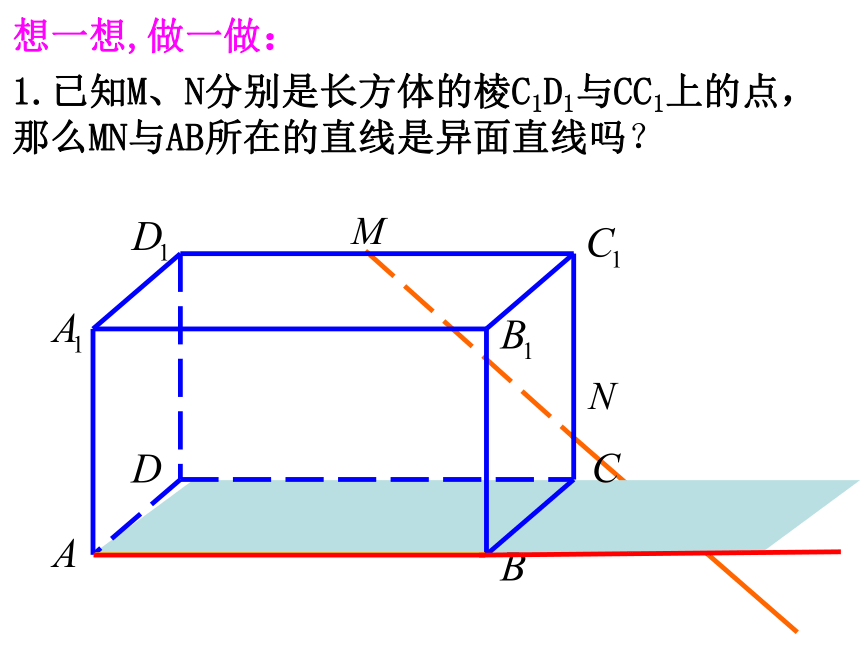
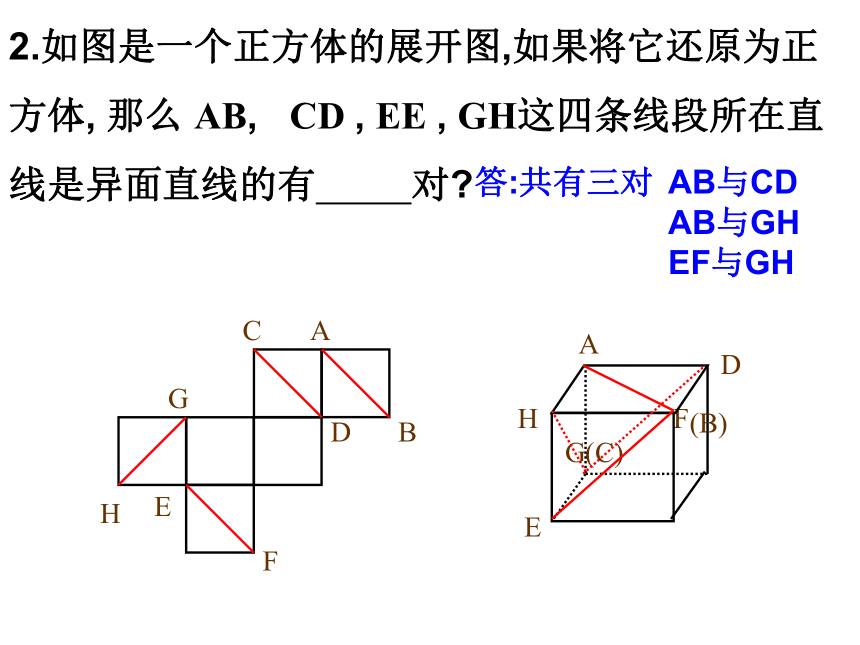
回答类似的问题.思考:我们把具有上述特征的两条直线取个怎样的名字才好呢?讲授新课一、空间中两条直线的位置关系思考: ,则 与 是异面直线吗?1.异面直线的定义: 我们把不同在任何一个平面内的两条直线叫做异面直线。(既不相交也不平行的两条直线)a与b是异面直线a与b是相交直线a与b是平行直线它们可能异面,可能相交,也可能平行。 说明: 画异面直线时 , 为了体现它们不共面的特点。常借助一个或两个平面来衬托。如图:(1)(3)(2)2.异面直线的画法:想一想,做一做:1.已知M、N分别是长方体的棱C1D1与CC1上的点,那么MN与AB所在的直线是异面直线吗?HGCADBEFGHEF(C)DA2.如图是一个正方体的展开图,如果将它还原为正方体, 那么 AB, CD , EE , GH这四条线段所在直线是异面直线的有 对?答:共有三对AB与CD
AB与GH
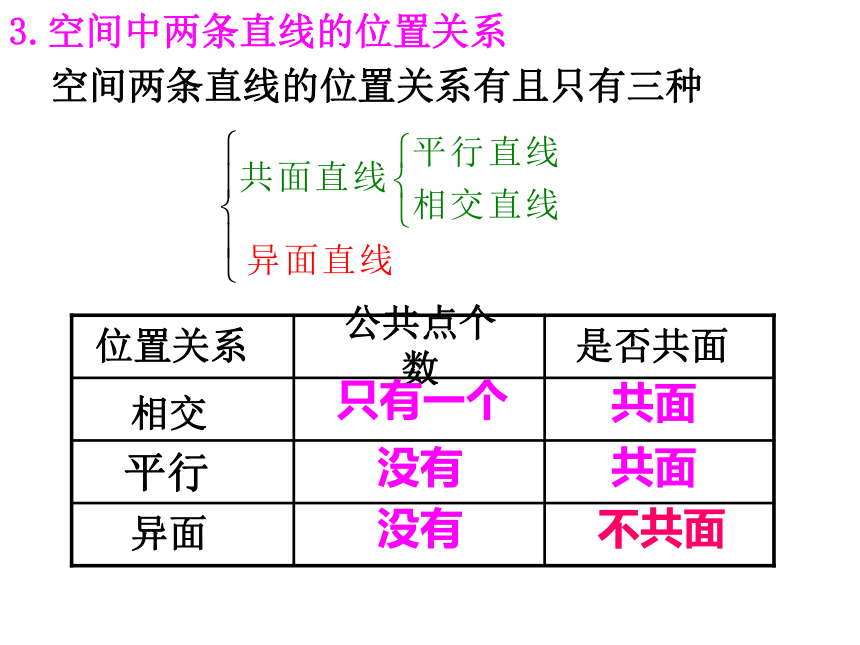
EF与GH(B)空间两条直线的位置关系有且只有三种没有只有一个没有共面不共面共面3.空间中两条直线的位置关系问题2:在同一平面内,平行于同一直线的两直线有什么位置关系?在空间这一规律是否还成立呢?二、空间直线的平行关系1、平行线的传递性公理4:平行于同一条直线的两条直线互相平行。——平行线的传递性作用:判断空间两条直线平行的依据。符号表示:设空间中的三条直线分别为a, b, c,a∥b
c∥ba∥c若例题分析例1: 在空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点。
求证:四边形EFGH是平行四边形。证明:连结BDE、F、G、H分别是各边中点EH ∥BD且EH = BD
FG ∥BD且FG = BDEFGH是一个平行四边形EH∥FG且EH=FG变式: 在例1中,如果再加上条件AC=BD,那么四边形EFGH是什么图形? EHFG分析:
在例题2的基础上我们只需要证明平行四边形的两条邻边相等。菱形问题3:在平面上,我们容易证明“如果一个角的两边和另一个角的两边分别平行,那么这两个角相等或互补”。在空间中,结论是否仍然成立呢?2、?等角定理等角定理:空间中如果两个角的两边分别对应平行,那么这两个角相等或互补。定理推论:如果两条相交直线和另两条相交直线分别平行,那么它们所成的锐角(或直角)相等.三、异面直线所成的角如图,已知两条异面直线a,b,经过空间任一点O作直线a'∥a,b'∥b,我们把a'与b'所成的锐角(或直角)叫做异面直线a,b所成的角(或夹角)。为了简便,点O通常取在两条异面直线中的一条上,例如,取在直线b上,然后经过点O作直线a'∥a,a'?和b所成的锐角(或直角)就是异面直线a与b所成的角。想一想:a'与b'?所成角的大小与点O的位置有关吗?1.?异面直线所成的角2.?异面垂直如果两条异面直线所成的角为直角,就说两条直线互相垂直,记作a⊥b。两条异面直线所成角的范围是(0°,90°]两直线垂直一定相交吗?不一定例2.如图,已知正方体ABCD-A'B'C'D'?中。
(1)哪些棱所在直线与直线BA'是异面直线?
(2)直线BA'?和CC'?的夹角是多少?
(3)哪些棱所在的直线与直线AA'?垂直?ABCDA'B'C'D'例题分析例2.如图,已知正方体ABCD-A'B'C'D'?中。
(1)哪些棱所在直线与直线BA'是异面直线?
(2)直线BA'?和CC'?的夹角是多少?
(3)哪些棱所在的直线与直线AA'?垂直?解:(2)由 可
知, 等于异面直线 与 的夹角,所以异面直线 与 的夹角为450 。 (3) 直线与直线 都垂直.ABCDA'B'C'D'1、解题时常将异面直线所成的角转化为相交直线所成的角实现了空间问题平面化题后反思:2、求异面直线所成角的步骤:一作(找):作(或找)平行线
二证:证明所作的角为所求的异
面直线所成的角。
三求:在一恰当的三角形中求出角巩固练习:1. 判断:
(1)垂直于同一直线的两条直线平行.( ?)
(2)若一个角的两边分别与另一个角的两边平行,那么这两个角相等( )××(3)平行于同一直线的两条直线平行.( )√(4)不在同一平面内的两条直线叫异面直线( )×1.异面直线的定义及其画法 课堂小结2.空间两直线的位置关系3.公理44.等角定理5.异面直线所成的角6.异面直线夹角的求法
直线之间的位置关系学习目标知识与技能:会判断空间两直线的位置关系,理解公理四,掌握异面直线的概念及所成的角。过程与方法:用实例引出异面直线的概念,介绍空间直线位置关系,进而由公理4引出异面直线所成的角。学习重点:空间两直线的位置关系及异面直线所成的角。学习难点:求异面直线所成的角。学习方法:类比式、探索启发式情感态度价值观:培养学生观察,发现,总结以及动手操作的能力,增强空间立体感。同一平面内两条直线的位置关系复习引入问题1:空间中没有公共点的两条直线一定平行吗?观察1:教室内讲桌的上边沿所在直线与黑板的左右两侧所在的直线,想一想:它们相交吗?平行吗?共面吗?观察2:长方体的棱A′B所在
直线与棱C′C所在直线,
回答类似的问题.思考:我们把具有上述特征的两条直线取个怎样的名字才好呢?讲授新课一、空间中两条直线的位置关系思考: ,则 与 是异面直线吗?1.异面直线的定义: 我们把不同在任何一个平面内的两条直线叫做异面直线。(既不相交也不平行的两条直线)a与b是异面直线a与b是相交直线a与b是平行直线它们可能异面,可能相交,也可能平行。 说明: 画异面直线时 , 为了体现它们不共面的特点。常借助一个或两个平面来衬托。如图:(1)(3)(2)2.异面直线的画法:想一想,做一做:1.已知M、N分别是长方体的棱C1D1与CC1上的点,那么MN与AB所在的直线是异面直线吗?HGCADBEFGHEF(C)DA2.如图是一个正方体的展开图,如果将它还原为正方体, 那么 AB, CD , EE , GH这四条线段所在直线是异面直线的有 对?答:共有三对AB与CD
AB与GH
EF与GH(B)空间两条直线的位置关系有且只有三种没有只有一个没有共面不共面共面3.空间中两条直线的位置关系问题2:在同一平面内,平行于同一直线的两直线有什么位置关系?在空间这一规律是否还成立呢?二、空间直线的平行关系1、平行线的传递性公理4:平行于同一条直线的两条直线互相平行。——平行线的传递性作用:判断空间两条直线平行的依据。符号表示:设空间中的三条直线分别为a, b, c,a∥b
c∥ba∥c若例题分析例1: 在空间四边形ABCD中,E,F,G,H分别是AB,BC,CD,DA的中点。
求证:四边形EFGH是平行四边形。证明:连结BDE、F、G、H分别是各边中点EH ∥BD且EH = BD
FG ∥BD且FG = BDEFGH是一个平行四边形EH∥FG且EH=FG变式: 在例1中,如果再加上条件AC=BD,那么四边形EFGH是什么图形? EHFG分析:
在例题2的基础上我们只需要证明平行四边形的两条邻边相等。菱形问题3:在平面上,我们容易证明“如果一个角的两边和另一个角的两边分别平行,那么这两个角相等或互补”。在空间中,结论是否仍然成立呢?2、?等角定理等角定理:空间中如果两个角的两边分别对应平行,那么这两个角相等或互补。定理推论:如果两条相交直线和另两条相交直线分别平行,那么它们所成的锐角(或直角)相等.三、异面直线所成的角如图,已知两条异面直线a,b,经过空间任一点O作直线a'∥a,b'∥b,我们把a'与b'所成的锐角(或直角)叫做异面直线a,b所成的角(或夹角)。为了简便,点O通常取在两条异面直线中的一条上,例如,取在直线b上,然后经过点O作直线a'∥a,a'?和b所成的锐角(或直角)就是异面直线a与b所成的角。想一想:a'与b'?所成角的大小与点O的位置有关吗?1.?异面直线所成的角2.?异面垂直如果两条异面直线所成的角为直角,就说两条直线互相垂直,记作a⊥b。两条异面直线所成角的范围是(0°,90°]两直线垂直一定相交吗?不一定例2.如图,已知正方体ABCD-A'B'C'D'?中。
(1)哪些棱所在直线与直线BA'是异面直线?
(2)直线BA'?和CC'?的夹角是多少?
(3)哪些棱所在的直线与直线AA'?垂直?ABCDA'B'C'D'例题分析例2.如图,已知正方体ABCD-A'B'C'D'?中。
(1)哪些棱所在直线与直线BA'是异面直线?
(2)直线BA'?和CC'?的夹角是多少?
(3)哪些棱所在的直线与直线AA'?垂直?解:(2)由 可
知, 等于异面直线 与 的夹角,所以异面直线 与 的夹角为450 。 (3) 直线与直线 都垂直.ABCDA'B'C'D'1、解题时常将异面直线所成的角转化为相交直线所成的角实现了空间问题平面化题后反思:2、求异面直线所成角的步骤:一作(找):作(或找)平行线
二证:证明所作的角为所求的异
面直线所成的角。
三求:在一恰当的三角形中求出角巩固练习:1. 判断:
(1)垂直于同一直线的两条直线平行.( ?)
(2)若一个角的两边分别与另一个角的两边平行,那么这两个角相等( )××(3)平行于同一直线的两条直线平行.( )√(4)不在同一平面内的两条直线叫异面直线( )×1.异面直线的定义及其画法 课堂小结2.空间两直线的位置关系3.公理44.等角定理5.异面直线所成的角6.异面直线夹角的求法
