人教版数学必修2 2.2.1 直线与平面平行(共27张ppt)
文档属性
| 名称 | 人教版数学必修2 2.2.1 直线与平面平行(共27张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 498.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-06 19:09:15 | ||
图片预览







文档简介
课件27张PPT。
直线与平面平行1、直线与直线的位置关系有哪几种?提示:从公共点的个数(出发思考)2、判断两条直线平行有几种方法?(结合图形)
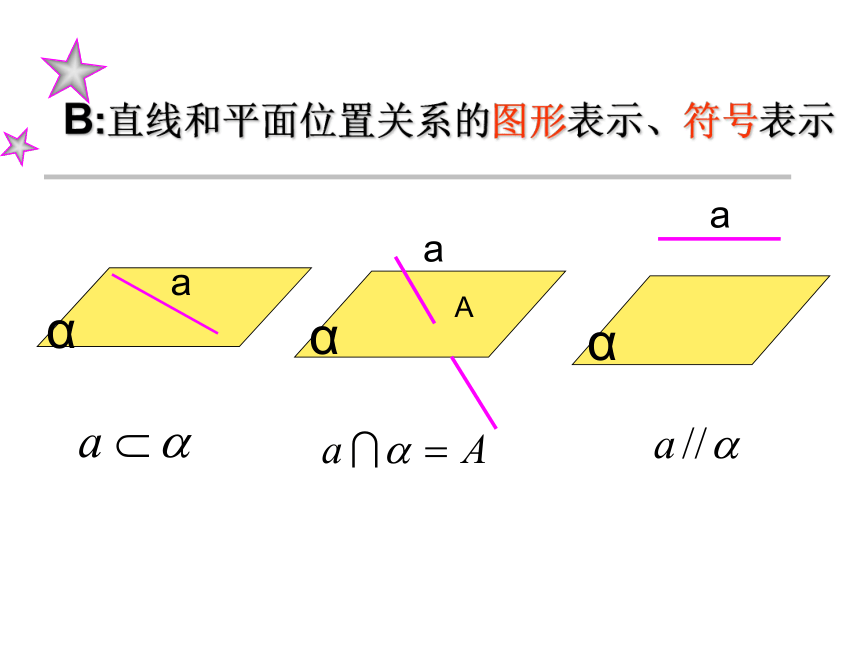
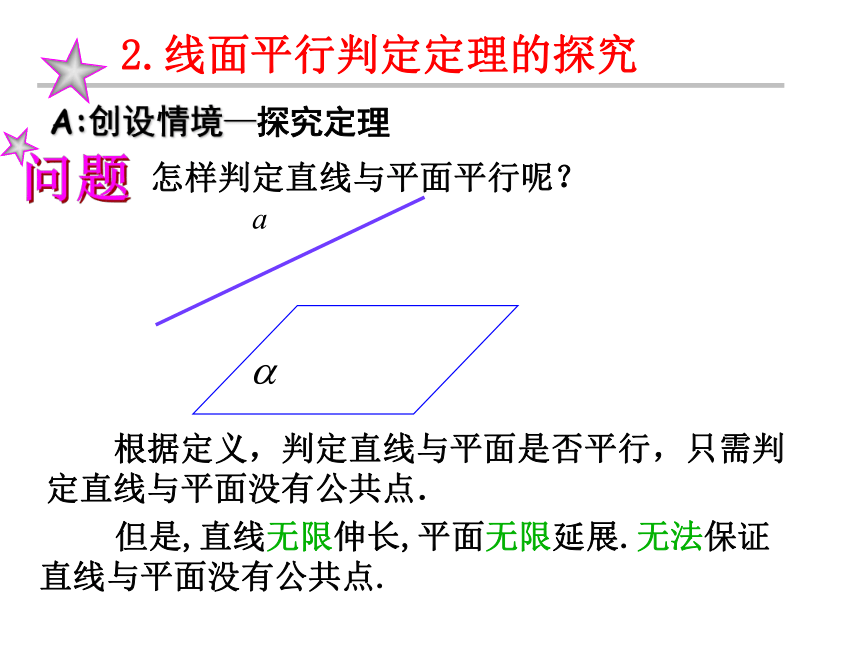
(1)三角形中位线定理;(2)平行四边形的对边;(3)成比例线段; (4)平行公理.一、知识回顾1、直线与平面的位置关系A:位置关系(1)有无数个公共点直线在平面内(2)有且只有一个公共点直线与平面相交(3)没有公共点直线与平面平行二、研探新知B:直线和平面位置关系的图形表示、符号表示 根据定义,判定直线与平面是否平行,只需判定直线与平面没有公共点. A:创设情境—探究定理怎样判定直线与平面平行呢?
问题 但是,直线无限伸长,平面无限延展.无法保证直线与平面没有公共点.
2.线面平行判定定理的探究实例感受实例感受 在生活中,注意到门扇的两边是平行的,当门扇绕着一边转动时,另一边始终与门框所在的平面没有公共点,此时门扇转动的一边与门框所在的平面给人以平行的印象.在门扇的旋转过程中:直线AB在门框所在的平面外直线CD在门框所在的平面内 直线AB与CD始终是平行的CABD实例感受观察1 将一本书平放在桌面上,翻动书的硬皮封面,封面边缘AB所在直线与桌面所在平面具有什么样的位置关系?实例感受观察2在封面翻动过程中:直线AB在桌面所在的平面外直线CD在桌面所在的平面内直线AB与CD始终是平行的实例感受把直角梯形泡沫互相平行的一边放在讲台桌面上并转动,观察另一边与桌面的位置给人以平行的感觉,而当把直角腰放在桌面上并转动,观察另一边与桌面给人的印象就不平行。 观察3实例感受2.线面平行判定定理的探究B:动手操作—猜想定理 问题2:翻开课本,封面边缘AB 与CD始终 平行吗?与桌面呢?
问题3:由边缘AB //CD ,翻动过程中边缘AB与桌面的平行关系,会发生变化吗?
由此你能得到什么结论?α2.线面平行判定的建构问题:能否用平面外一条直线平行于平面内直线,来判断这条直线与这个平面平行呢? C:观察分析—归纳定理 2.线面平行判定定理的探究 直线与平面平行,关键是三个要素:
(1) 平面外一条线
(2) 平面内一条直线
(3) 这两条直线平行D:动脑思考—确认定理2.直线与平面平行的判定定理 A:判定定理
平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.判定或证明线面平行。B:定理说明在平面内找(或作)出一条直线与面外的直线平行。
空间问题转化为平面问题。1、作用:2、关键:3、思想: C:理论提升
判定定理的三个条件缺一不可简记为:线线平行则线面平行 直线与平面平行关系直线间平行关系空间问题平面问题想一想
(1)与AB平行的平面是 ;(2)与 平行的平面是 ;(3)与AD平行的平面是 ; 1、如图,长方体 中, 例1.空间四边形ABCD中,E,F分别为AB,AD的中点,证明:直线EF与平面BCD平行证明:如右图,连接BD,∴EF ∥平面BCD∴EF ∥BD,
∴在△ABD中,E,F分别为AB,
AD的中点,即EF为中位线例题讲解:大图小结:在平面内找(作)一条直线与平面外的直线平行时可以通过
三角形的中位线、梯形的中位线、平行线的性质等来完成。
________________. 如图,在空间四边形ABCD中,E、F
分别为AB、AD上的点,若 ,
则EF与平面BCD的位置关系是EF//平面BCDABCDEF平行线的判定定理,
变式训练1、如图,正方体ABCD-A1B1C1D1中,E为 DD1的中点,证明BD1∥平面AEC.证明:连结BD交AC于O,连结EO∵E,O分别为DD1与BD的中点∴BD1 ∥平面AEC巩固练习: 在△BDD1中∴EO∥BD1例2、如图,在正方体ABCD——A1B1C1D1中,E、F分别是棱BC与C1D1的中点。
求证:EF//平面BDD1B1.MNM例题讲解:PABCDEMN2、在四棱锥P—ABCD中,底面ABCD为平行四边形,N为PB 的中点,E为AD中点。
求证:EN//平面PDC巩固练习:A自我检测2.证明直线与平面平行的方法:(1)利用定义.(2)利用判定定理.3.数学思想方法:转化的思想知识小结直线与平面没有公共点1、直线与平面的位置关系变式E 2.如图,四棱锥A—DBCE中,O为底面正方形DBCE对角线的交点,F为AE的中点. 求证:AB//平面DCF.变式E3. 在图中所示的一块木料中,棱BC平行于面A′C′ .
(1)要经过面A′C′内的一点P和棱BC将木料锯开,应怎样画线?
(2)所画的线和面AC是什么位置关系?
(1)三角形中位线定理;(2)平行四边形的对边;(3)成比例线段; (4)平行公理.一、知识回顾1、直线与平面的位置关系A:位置关系(1)有无数个公共点直线在平面内(2)有且只有一个公共点直线与平面相交(3)没有公共点直线与平面平行二、研探新知B:直线和平面位置关系的图形表示、符号表示 根据定义,判定直线与平面是否平行,只需判定直线与平面没有公共点. A:创设情境—探究定理怎样判定直线与平面平行呢?
问题 但是,直线无限伸长,平面无限延展.无法保证直线与平面没有公共点.
2.线面平行判定定理的探究实例感受实例感受 在生活中,注意到门扇的两边是平行的,当门扇绕着一边转动时,另一边始终与门框所在的平面没有公共点,此时门扇转动的一边与门框所在的平面给人以平行的印象.在门扇的旋转过程中:直线AB在门框所在的平面外直线CD在门框所在的平面内 直线AB与CD始终是平行的CABD实例感受观察1 将一本书平放在桌面上,翻动书的硬皮封面,封面边缘AB所在直线与桌面所在平面具有什么样的位置关系?实例感受观察2在封面翻动过程中:直线AB在桌面所在的平面外直线CD在桌面所在的平面内直线AB与CD始终是平行的实例感受把直角梯形泡沫互相平行的一边放在讲台桌面上并转动,观察另一边与桌面的位置给人以平行的感觉,而当把直角腰放在桌面上并转动,观察另一边与桌面给人的印象就不平行。 观察3实例感受2.线面平行判定定理的探究B:动手操作—猜想定理 问题2:翻开课本,封面边缘AB 与CD始终 平行吗?与桌面呢?
问题3:由边缘AB //CD ,翻动过程中边缘AB与桌面的平行关系,会发生变化吗?
由此你能得到什么结论?α2.线面平行判定的建构问题:能否用平面外一条直线平行于平面内直线,来判断这条直线与这个平面平行呢? C:观察分析—归纳定理 2.线面平行判定定理的探究 直线与平面平行,关键是三个要素:
(1) 平面外一条线
(2) 平面内一条直线
(3) 这两条直线平行D:动脑思考—确认定理2.直线与平面平行的判定定理 A:判定定理
平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行.判定或证明线面平行。B:定理说明在平面内找(或作)出一条直线与面外的直线平行。
空间问题转化为平面问题。1、作用:2、关键:3、思想: C:理论提升
判定定理的三个条件缺一不可简记为:线线平行则线面平行 直线与平面平行关系直线间平行关系空间问题平面问题想一想
(1)与AB平行的平面是 ;(2)与 平行的平面是 ;(3)与AD平行的平面是 ; 1、如图,长方体 中, 例1.空间四边形ABCD中,E,F分别为AB,AD的中点,证明:直线EF与平面BCD平行证明:如右图,连接BD,∴EF ∥平面BCD∴EF ∥BD,
∴在△ABD中,E,F分别为AB,
AD的中点,即EF为中位线例题讲解:大图小结:在平面内找(作)一条直线与平面外的直线平行时可以通过
三角形的中位线、梯形的中位线、平行线的性质等来完成。
________________. 如图,在空间四边形ABCD中,E、F
分别为AB、AD上的点,若 ,
则EF与平面BCD的位置关系是EF//平面BCDABCDEF平行线的判定定理,
变式训练1、如图,正方体ABCD-A1B1C1D1中,E为 DD1的中点,证明BD1∥平面AEC.证明:连结BD交AC于O,连结EO∵E,O分别为DD1与BD的中点∴BD1 ∥平面AEC巩固练习: 在△BDD1中∴EO∥BD1例2、如图,在正方体ABCD——A1B1C1D1中,E、F分别是棱BC与C1D1的中点。
求证:EF//平面BDD1B1.MNM例题讲解:PABCDEMN2、在四棱锥P—ABCD中,底面ABCD为平行四边形,N为PB 的中点,E为AD中点。
求证:EN//平面PDC巩固练习:A自我检测2.证明直线与平面平行的方法:(1)利用定义.(2)利用判定定理.3.数学思想方法:转化的思想知识小结直线与平面没有公共点1、直线与平面的位置关系变式E 2.如图,四棱锥A—DBCE中,O为底面正方形DBCE对角线的交点,F为AE的中点. 求证:AB//平面DCF.变式E3. 在图中所示的一块木料中,棱BC平行于面A′C′ .
(1)要经过面A′C′内的一点P和棱BC将木料锯开,应怎样画线?
(2)所画的线和面AC是什么位置关系?
