人教版数学必修1 2.2 对数函数及其性质(共16张ppt)
文档属性
| 名称 | 人教版数学必修1 2.2 对数函数及其性质(共16张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 333.4KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-06 20:48:50 | ||
图片预览



文档简介
课件16张PPT。2.2 对数函数及其性质 考古学家经过长期实践,发现冻土层内某微量元素的含量P与年份t的关系:由指数与对数的关系,此指数式写成对数式是: 考古学家提取了冻土层内微量元素,确定它的残余量约占原始含量的1%,即 P=0.01 概念引入
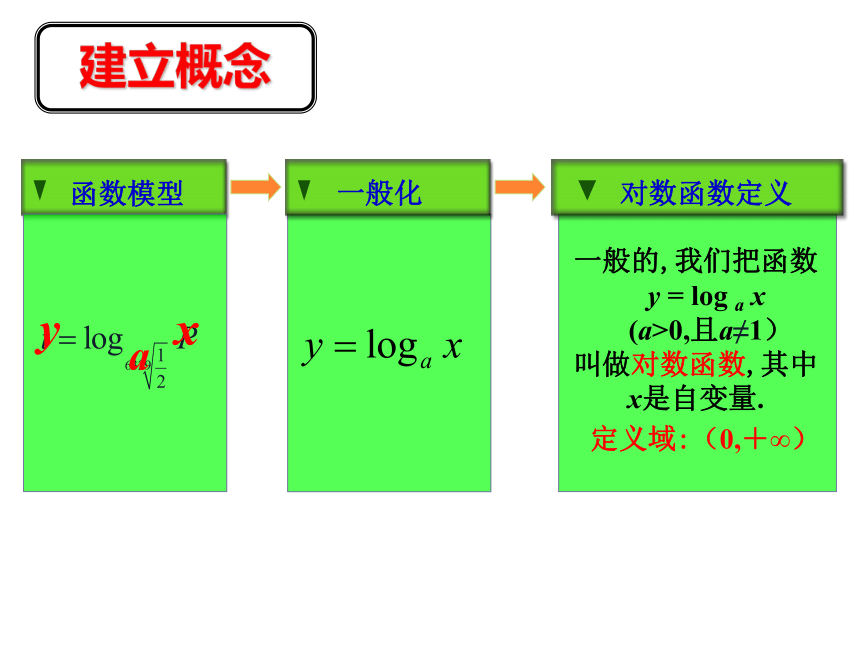
建立概念xya一般的,我们把函数
y = log a x
(a>0,且a≠1)
叫做对数函数,其中
x是自变量.定义域:(0,+∞)小结:求形如 的函数的定 义域要考虑________ 例1 求下列函数的定义域:典型例题 (2) ∵x2>0,即x≠0.
∴函数的定义域为{x| x≠0 }. (1) ∵4-x>0,即x<4.
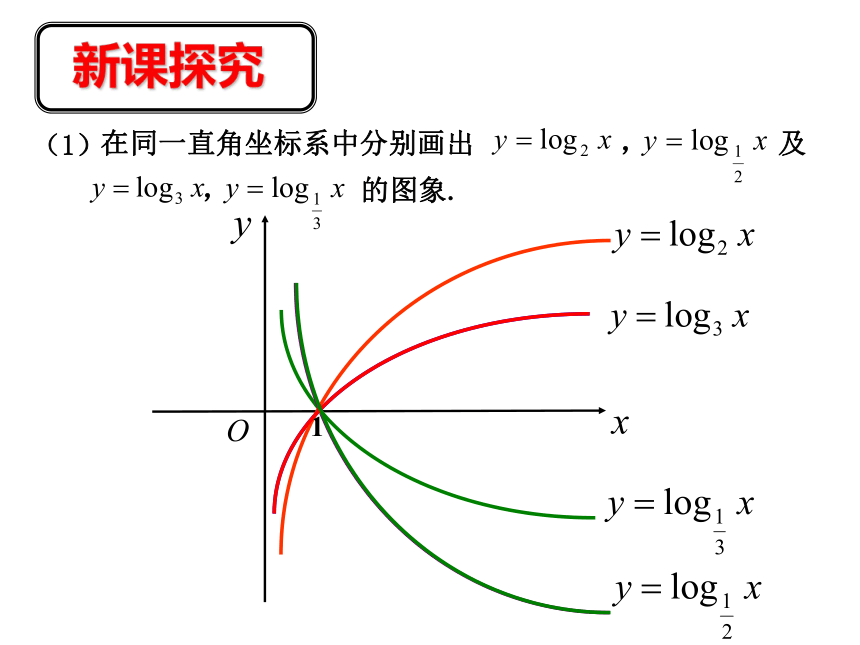
∴函数的定义域为{x| x<4 }. 解:在同一直角坐标系中分别画出 , 及
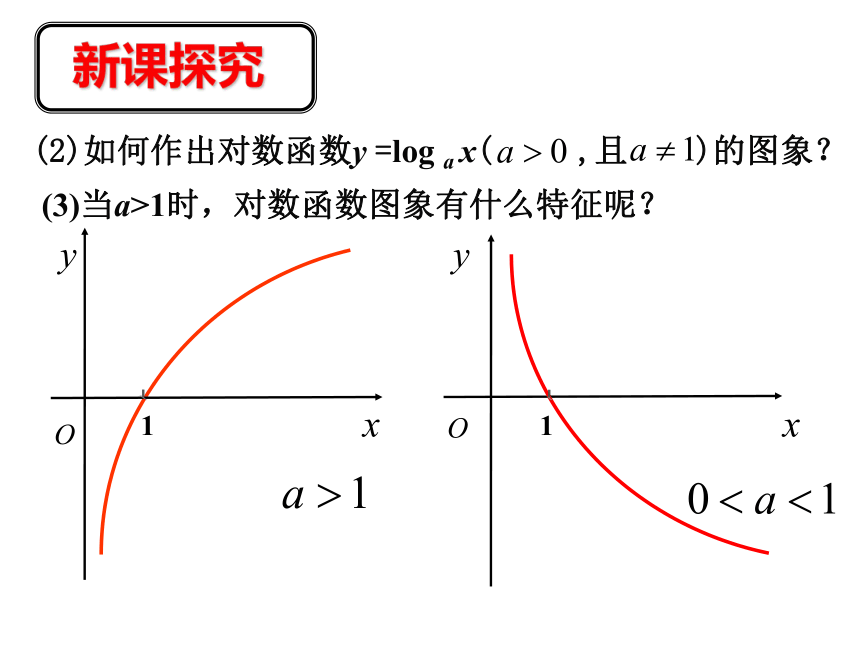
, 的图象.1新课探究(1)1新课探究(2)如何作出对数函数y =log a x( ,且 )的图象?(3)当a>1时,对数函数图象有什么特征呢?1
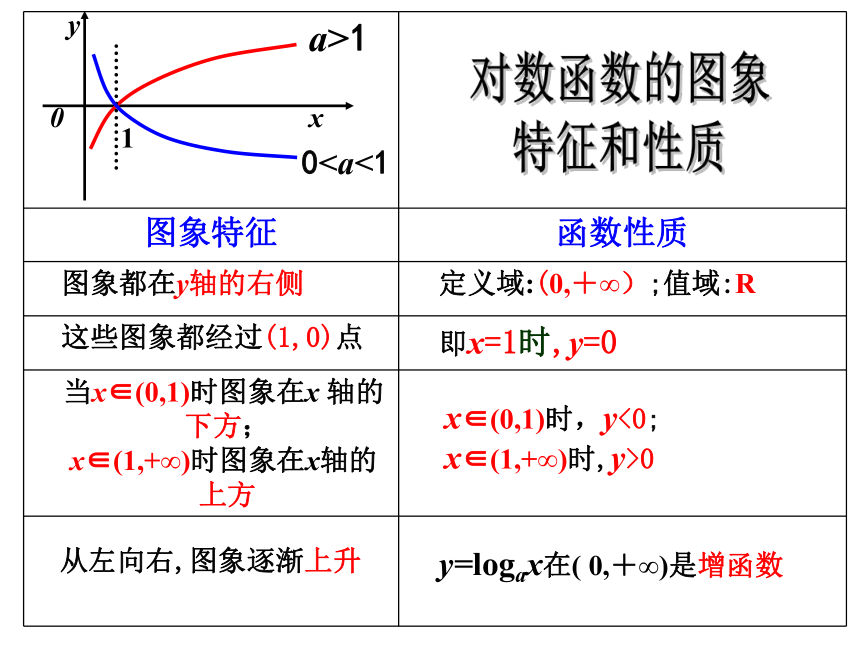
x01a>1y对数函数的图象
特征和性质即x=1时,y=0定义域:(0,+∞);值域:R x∈(0,1)时,y<0;
x∈(1,+∞)时,y>0y=logax在( 0,+∞)是增函数从左向右,图象逐渐上升
01时, x∈(0,1)时,y<0;
x∈(1,+∞)时,y>0.
当00;
x∈(1,+∞)时,y<0. x01a>10 是减函数.01xy定义域:( 0,+∞);值域:R.过定点(1,0)即x=1时,y=0.当a>1时,y=logax在( 0,+∞)
是增函数.对数函数y= log a x(a>0,且a≠1)的图象与性质探究延伸当a∈ (1,+∞)时,
x ∈ (1,+∞)时,y>0;
x ∈(0,1)时,y<0.
当a ∈(0,1)时,
x ∈(0,1)时,y>0;
x ∈(1,+∞)时,y<0.
(1)这个对数性质有什么规律?探讨对数log a x(a>0,a≠1,x>0)中a,x,y的符号规律.xy01a>10 2.体现了函数单调性的应用. log a3.4和 log a8.5(a>0,且a≠1)log 0.33.4 log 0.38.5> log a3.4和 log a8.5(a>0,且a≠1)例2. 比较下列两个数的大小:log 23.4 log 28.5log 0.33.4 log 0.38.5讲解范例<> 练习1.比较下列两个数的大小:<><>< 练习2.比较下列两个数的大小:> 小结:“介值法”体现了问题的转化思想. 想一想1.对数函数的定义;2.对数函数的图象和性质;3.对数函数的三个结论;4.对数函数的图象和性质的应用.
建立概念xya一般的,我们把函数
y = log a x
(a>0,且a≠1)
叫做对数函数,其中
x是自变量.定义域:(0,+∞)小结:求形如 的函数的定 义域要考虑________ 例1 求下列函数的定义域:典型例题 (2) ∵x2>0,即x≠0.
∴函数的定义域为{x| x≠0 }. (1) ∵4-x>0,即x<4.
∴函数的定义域为{x| x<4 }. 解:在同一直角坐标系中分别画出 , 及
, 的图象.1新课探究(1)1新课探究(2)如何作出对数函数y =log a x( ,且 )的图象?(3)当a>1时,对数函数图象有什么特征呢?1
x01a>1y对数函数的图象
特征和性质即x=1时,y=0定义域:(0,+∞);值域:R x∈(0,1)时,y<0;
x∈(1,+∞)时,y>0y=logax在( 0,+∞)是增函数从左向右,图象逐渐上升
0
x∈(1,+∞)时,y>0.
当0
x∈(1,+∞)时,y<0. x01a>10
是增函数.对数函数y= log a x(a>0,且a≠1)的图象与性质探究延伸当a∈ (1,+∞)时,
x ∈ (1,+∞)时,y>0;
x ∈(0,1)时,y<0.
当a ∈(0,1)时,
x ∈(0,1)时,y>0;
x ∈(1,+∞)时,y<0.
(1)这个对数性质有什么规律?探讨对数log a x(a>0,a≠1,x>0)中a,x,y的符号规律.xy01a>10
