人教版数学必修1 3.1.2 用二分法求方程的近似解(共13张ppt)
文档属性
| 名称 | 人教版数学必修1 3.1.2 用二分法求方程的近似解(共13张ppt) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.5MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-06 00:00:00 | ||
图片预览



文档简介
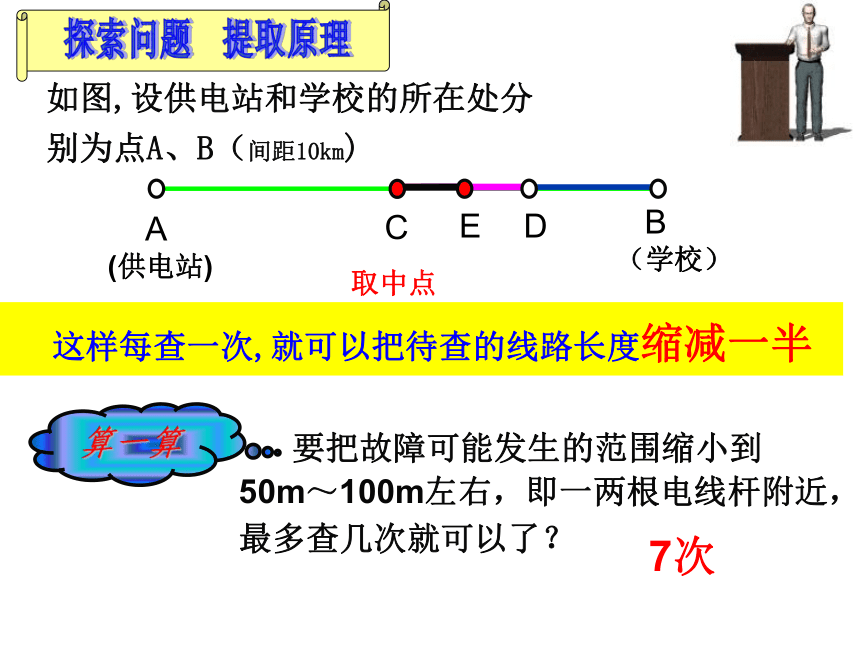
课件13张PPT。§3.1.2 用二分法求方程的近似解 如果沿着线路一小段一小段查找,困难很多。每查一个点要爬一次电线杆子,10km长,大约有200根电线杆子。如图,设供电站和学校的所在处分别为点A、B(间距10km) 这样每查一次,就可以把待查的线路长度缩减一半7次取中点探索问题 提取原理回顾旧知问题1:你能求下面方程的解吗?问题2:能不能确定方程 的根
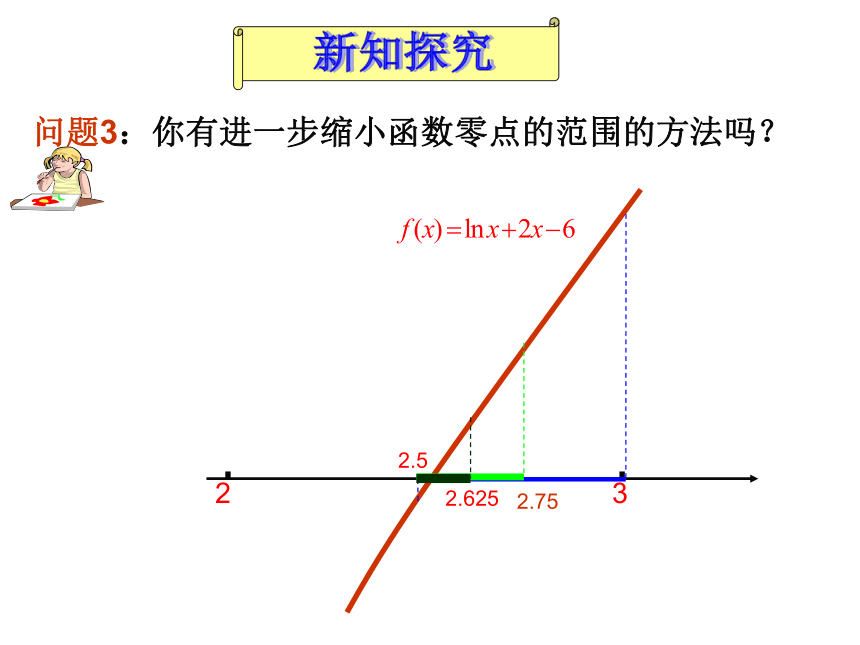
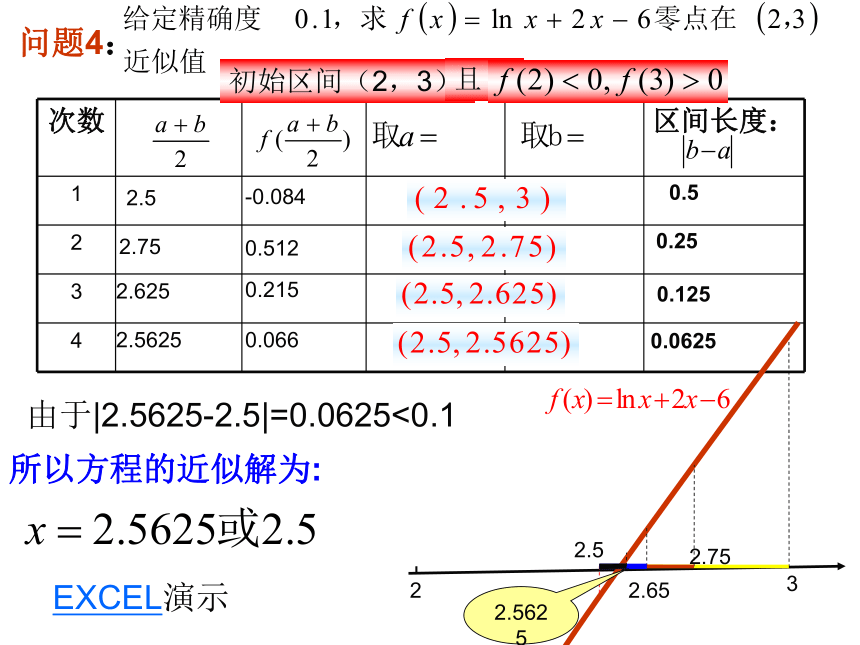
的大概范围呢? 问题3:你有进一步缩小函数零点的范围的方法吗? 新知探究0.5所以方程的近似解为:2.5-0.0842.530.250.1250.06252.750.5122.6250.2150.0662.56252.52.752 3由于|2.5625-2.5|=0.0625<0.12.52.752.652.5625 问题4: EXCEL演示二分法的定义:想一想?用二分法求函数零点近似值的
步骤是什么?
概念形成1.确定区间[a,b],验证f(a)·f(b)<0,给定精确度ε;3.计算f(c); 2.求区间(a,b)的中点c; (1)若f(c)=0,则c就是函数的零点;(2)若f(a)· f(c)<0,则令b= c(此时零点x0∈(a, c) );(3)若f(c)· f(b)<0,则令a= c(此时零点x0∈( c, b) ).4.判断是否达到精确度ε:即若|a-b|<ε,则得到零点近似值a(或b);否则重复步骤2~4.探究归纳实践探究解: 记函数演示例2:借用计算器或计算机用二分法求方程
的近似解(精确度0.1)应用新知 实践巩固0ADcB练习:下列函数的图像中,其中不能用二分法求解其零点的是( )概念拓展 实践探究1、什么是二分法?
2、具有怎样特征的函数零点不能用二分法求得?
3、二分法求函数零点的步骤是什么?反思小结 体会收获确定初始区间 取中点求值并缩小区间 求区间长度 比较精确度 下结论YN反思小结 体会收获课后作业:1、课本92页习题3.1 4(用计算器)、5(上机操作)2、阅读课本91页《中外历史上的方程求解》巩固提高 课外练习
的大概范围呢? 问题3:你有进一步缩小函数零点的范围的方法吗? 新知探究0.5所以方程的近似解为:2.5-0.0842.530.250.1250.06252.750.5122.6250.2150.0662.56252.52.752 3由于|2.5625-2.5|=0.0625<0.12.52.752.652.5625 问题4: EXCEL演示二分法的定义:想一想?用二分法求函数零点近似值的
步骤是什么?
概念形成1.确定区间[a,b],验证f(a)·f(b)<0,给定精确度ε;3.计算f(c); 2.求区间(a,b)的中点c; (1)若f(c)=0,则c就是函数的零点;(2)若f(a)· f(c)<0,则令b= c(此时零点x0∈(a, c) );(3)若f(c)· f(b)<0,则令a= c(此时零点x0∈( c, b) ).4.判断是否达到精确度ε:即若|a-b|<ε,则得到零点近似值a(或b);否则重复步骤2~4.探究归纳实践探究解: 记函数演示例2:借用计算器或计算机用二分法求方程
的近似解(精确度0.1)应用新知 实践巩固0ADcB练习:下列函数的图像中,其中不能用二分法求解其零点的是( )概念拓展 实践探究1、什么是二分法?
2、具有怎样特征的函数零点不能用二分法求得?
3、二分法求函数零点的步骤是什么?反思小结 体会收获确定初始区间 取中点求值并缩小区间 求区间长度 比较精确度 下结论YN反思小结 体会收获课后作业:1、课本92页习题3.1 4(用计算器)、5(上机操作)2、阅读课本91页《中外历史上的方程求解》巩固提高 课外练习
