人教版数学必修二 4.2.2 圆与圆的位置关系(共21张ppt)
文档属性
| 名称 | 人教版数学必修二 4.2.2 圆与圆的位置关系(共21张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 500.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-06 22:32:21 | ||
图片预览







文档简介
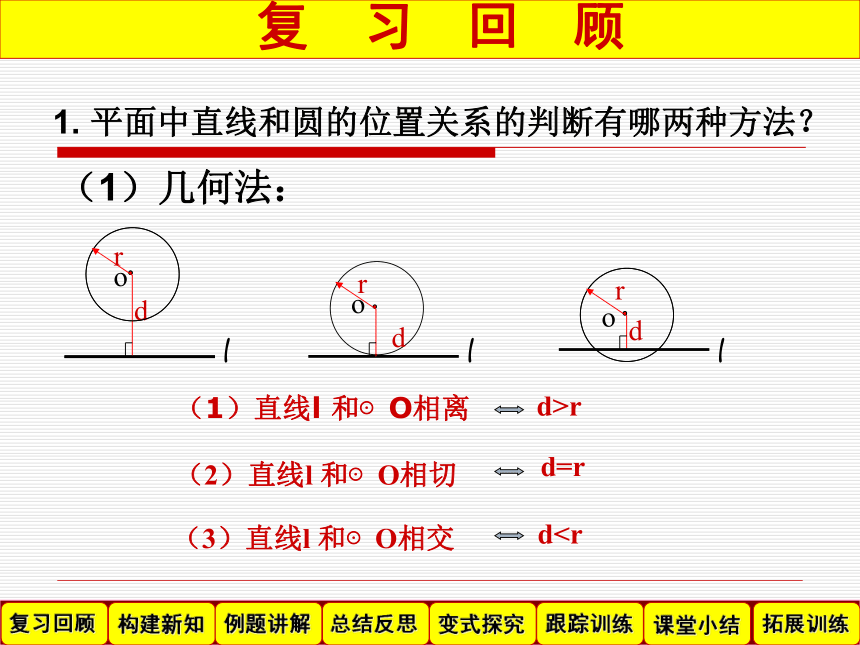
课件21张PPT。数 学2普 通 高 中 课 程 准 实 验 教 科 书必 修A人民教育出版社版4.2.2 圆与圆的位置关系(2)直线l 和⊙O相切 (1)直线l 和⊙O相离(3)直线l 和⊙O相交d>rd=rd0 则直线与圆相交。(2)代数法:1. 平面中直线和圆的位置关系的判断有那两种方法?若直线方程为: ,圆方程为:
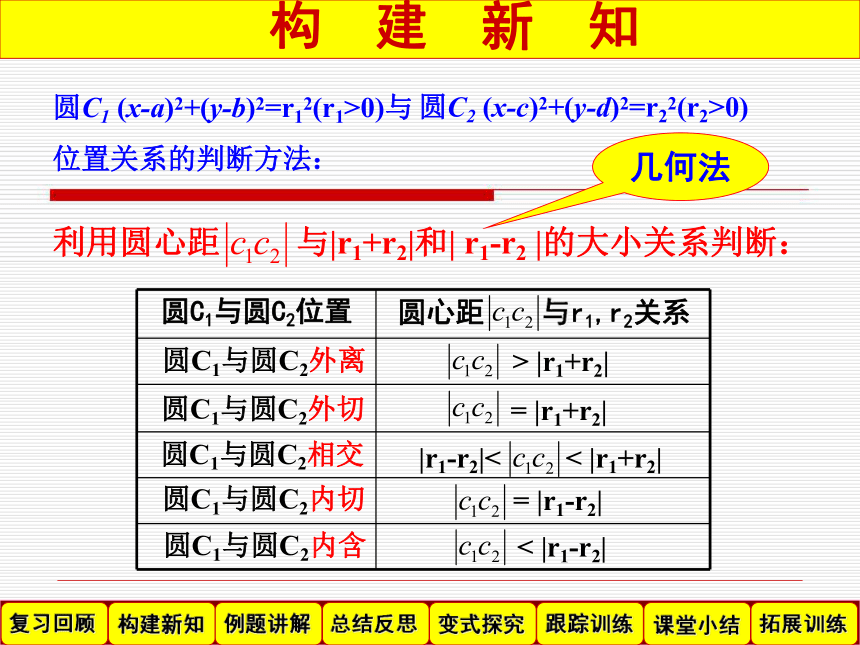
由 消元得到关于 或 的一元二次方程复 习 回 顾2.圆与圆的位置关系有哪几种?相离、外切、相交、内切、内含复 习 回 顾构 建 新 知利用圆心距 与|r1+r2|和| r1-r2 |的大小关系判断:几何法圆C1与圆C2位置圆心距 与r1,r2关系圆C1与圆C2外离圆C1与圆C2外切圆C1与圆C2相交圆C1与圆C2内切圆C1与圆C2内含 > |r1+r2| < |r1-r2||r1-r2|< < |r1+r2| = |r1-r2| = |r1+r2|例1.已知圆C1 : x2+y2+2x+8y-8=0和圆C2 :
x2+y2-4x-4y-2=0,试判断圆C1与圆C2的
位置关系.例 题 讲 解例 题 讲 解解法一: 把圆C1的方程化为标准方程,得
圆C1的圆心是点(-1,-4),半径长r1=5.
把圆C2的方程化为标准方程,得
圆C1的圆心是点(2,2),半径长r2= .
圆C1与圆C2的连心线长为
圆C1与圆C2的半径之和是
两半径之差是
所以圆C1与圆C2相交,他们有两个公共点A,B. 例1.已知圆C1:x2+y2+2x+8y-8=0和圆C2:x2+y2-4x-4y-2=0,
试判断圆C1与圆C2的位置关系.例1.已知圆C1 : x2+y2+2x+8y-8=0和圆C2 :
x2+y2-4x-4y-2=0,试判断圆C1与圆C2的
位置关系.例 题 讲 解思考?类比“判断直线与圆的位置关系中的代数法”,你能用两圆的方程来判断这两个圆的位置关系吗?例 题 讲 解①-②,得 x+2y-1=0, ③
由③得:解法二:圆C1与圆C2的方程联立,得到方程组
①
②把上式代入①,并整理,得 ④方程④的判别式所以,方程④有两个不相等的实数根x1,x2分别代入方程③,得到y1,y2.
因此圆C1与圆C2有两个不同的公共点A(x1,y1),B(x2,y2).
所以两圆相交.利用两个圆的方程组成方程组的实数解的个数:代数法构 建 新 知△<0△=0△>0012跟 踪 训 练判断圆 与圆 的位置关系.(分别用几何法和代数法)两 圆 相 外 离总 结 反 思圆与圆位置关系两种判断方法的总结反思1.总结:利用圆心距 与|r1+r2|和| r1-r2 |的大小关系判断:(1)几何法圆C1与圆C2位置圆心距 与r1,r2关系圆C1与圆C2外离圆C1与圆C2外切圆C1与圆C2相交圆C1与圆C2内切圆C1与圆C2内含 > |r1+r2| < |r1-r2||r1-r2|< < |r1+r2| = |r1-r2| = |r1+r2|总 结 反 思1.总结:(2)代数法利用两个圆的方程组成方程组的实数解的个数:△<0△=0△>0012圆与圆位置关系两种判断方法的总结反思总 结 反 思2.反思:几何法和代数法各有优劣,如何选用?代数方法:能求出交点,但是当Δ=0,Δ<0时,不能
判断两圆的位置关系。几何方法:形象直观、运算简便,但不能求出交点;圆与圆位置关系两种判断方法的总结反思变 式 探 究例1:已知圆C1:x2+y2+2x+8y-8=0和圆C2:x2+y2-4x-4y-2=0,
试判断圆C1与圆C2的位置关系.变式1:求这两个圆的公共弦所在的直线的方程.变 式 探 究例1:已知圆C1:x2+y2+2x+8y-8=0和圆C2:x2+y2-4x-4y-2=0,试判断
圆C1与圆C2的位置关系.变式1:求这两个圆的公共弦所在的直线的方程.答案:①-②,得 x + 2y – 1 = 0 , ③ 得: 解法二:圆C1与圆C2的方程联立,得到方程组
①
②把上式代入①,并整理,得: ④方程④的判别式:所以,方程④有两个不相等的实数根x1,x2分别代入方程③,得到y1,y2.
因此圆C1与圆C2有两个不同的公共点A(x1,y1),B(x2,y2).所以两圆相交.直线AB的方程:
【方法总结】
已知两个圆的方程: 与
,则两圆的公共弦所在直
线方程为两圆方程相减:
变式2:求这两个圆的公共弦长.变 式 探 究例1:已知圆C1:x2+y2+2x+8y-8=0和圆C2:x2+y2-4x-4y-2=0,
试判断圆C1与圆C2的位置关系.答案:方法一:求交点;方法二:转化为求圆的弦长。跟 踪 训 练(2).若圆:x2+y2–2x–5=0和圆:x2+y2+2x–4y–4=0
的交点为A,B,则线段AB的垂直平分线的
方程是( )
A. x+y–1=0 B. 2x–y+1=0
C. x–2y+1=0 D. x–y+1=0A(1).两圆x2+y2–2x-1=0与x2+y2–4y=0的公共弦所在直线的方程是_____________________.
.
2x-4y+1=0(3).过两圆x2+y2+6x-4=0和x2+y2+6y-28=0的交点
且圆心在直线x-y-4=0上的圆方程是( )
A.x2+y2-x-5y+2=0
B.x2+y2-x-5y-2=0
C.x2+y2-x+7y-32=0
D.x2+y2+x+7y+32=0
跟 踪 训 练C课 堂 小 结1.本节课你收获了什么?(1)知识方面:(2)数学思想方面:判断圆与圆的位置关系的两种方法,以及这两种方法的优劣。求圆与圆相交弦所在直线方程的方法。求圆与圆相交弦的弦长的方法。数形结合的思想,等价转化的思想,类比思想。1.圆A:x2+y2=25和圆B:x2+(y-6)2=1的位 置关系
是 ________
2.圆x2+y2=a(a>0)与x2+y2+6x-8y-11=0相内切,则
实数a的值为________答案:1、外切; 2、1或121拓 展 练 习
由 消元得到关于 或 的一元二次方程复 习 回 顾2.圆与圆的位置关系有哪几种?相离、外切、相交、内切、内含复 习 回 顾构 建 新 知利用圆心距 与|r1+r2|和| r1-r2 |的大小关系判断:几何法圆C1与圆C2位置圆心距 与r1,r2关系圆C1与圆C2外离圆C1与圆C2外切圆C1与圆C2相交圆C1与圆C2内切圆C1与圆C2内含 > |r1+r2| < |r1-r2||r1-r2|< < |r1+r2| = |r1-r2| = |r1+r2|例1.已知圆C1 : x2+y2+2x+8y-8=0和圆C2 :
x2+y2-4x-4y-2=0,试判断圆C1与圆C2的
位置关系.例 题 讲 解例 题 讲 解解法一: 把圆C1的方程化为标准方程,得
圆C1的圆心是点(-1,-4),半径长r1=5.
把圆C2的方程化为标准方程,得
圆C1的圆心是点(2,2),半径长r2= .
圆C1与圆C2的连心线长为
圆C1与圆C2的半径之和是
两半径之差是
所以圆C1与圆C2相交,他们有两个公共点A,B. 例1.已知圆C1:x2+y2+2x+8y-8=0和圆C2:x2+y2-4x-4y-2=0,
试判断圆C1与圆C2的位置关系.例1.已知圆C1 : x2+y2+2x+8y-8=0和圆C2 :
x2+y2-4x-4y-2=0,试判断圆C1与圆C2的
位置关系.例 题 讲 解思考?类比“判断直线与圆的位置关系中的代数法”,你能用两圆的方程来判断这两个圆的位置关系吗?例 题 讲 解①-②,得 x+2y-1=0, ③
由③得:解法二:圆C1与圆C2的方程联立,得到方程组
①
②把上式代入①,并整理,得 ④方程④的判别式所以,方程④有两个不相等的实数根x1,x2分别代入方程③,得到y1,y2.
因此圆C1与圆C2有两个不同的公共点A(x1,y1),B(x2,y2).
所以两圆相交.利用两个圆的方程组成方程组的实数解的个数:代数法构 建 新 知△<0△=0△>0012跟 踪 训 练判断圆 与圆 的位置关系.(分别用几何法和代数法)两 圆 相 外 离总 结 反 思圆与圆位置关系两种判断方法的总结反思1.总结:利用圆心距 与|r1+r2|和| r1-r2 |的大小关系判断:(1)几何法圆C1与圆C2位置圆心距 与r1,r2关系圆C1与圆C2外离圆C1与圆C2外切圆C1与圆C2相交圆C1与圆C2内切圆C1与圆C2内含 > |r1+r2| < |r1-r2||r1-r2|< < |r1+r2| = |r1-r2| = |r1+r2|总 结 反 思1.总结:(2)代数法利用两个圆的方程组成方程组的实数解的个数:△<0△=0△>0012圆与圆位置关系两种判断方法的总结反思总 结 反 思2.反思:几何法和代数法各有优劣,如何选用?代数方法:能求出交点,但是当Δ=0,Δ<0时,不能
判断两圆的位置关系。几何方法:形象直观、运算简便,但不能求出交点;圆与圆位置关系两种判断方法的总结反思变 式 探 究例1:已知圆C1:x2+y2+2x+8y-8=0和圆C2:x2+y2-4x-4y-2=0,
试判断圆C1与圆C2的位置关系.变式1:求这两个圆的公共弦所在的直线的方程.变 式 探 究例1:已知圆C1:x2+y2+2x+8y-8=0和圆C2:x2+y2-4x-4y-2=0,试判断
圆C1与圆C2的位置关系.变式1:求这两个圆的公共弦所在的直线的方程.答案:①-②,得 x + 2y – 1 = 0 , ③ 得: 解法二:圆C1与圆C2的方程联立,得到方程组
①
②把上式代入①,并整理,得: ④方程④的判别式:所以,方程④有两个不相等的实数根x1,x2分别代入方程③,得到y1,y2.
因此圆C1与圆C2有两个不同的公共点A(x1,y1),B(x2,y2).所以两圆相交.直线AB的方程:
【方法总结】
已知两个圆的方程: 与
,则两圆的公共弦所在直
线方程为两圆方程相减:
变式2:求这两个圆的公共弦长.变 式 探 究例1:已知圆C1:x2+y2+2x+8y-8=0和圆C2:x2+y2-4x-4y-2=0,
试判断圆C1与圆C2的位置关系.答案:方法一:求交点;方法二:转化为求圆的弦长。跟 踪 训 练(2).若圆:x2+y2–2x–5=0和圆:x2+y2+2x–4y–4=0
的交点为A,B,则线段AB的垂直平分线的
方程是( )
A. x+y–1=0 B. 2x–y+1=0
C. x–2y+1=0 D. x–y+1=0A(1).两圆x2+y2–2x-1=0与x2+y2–4y=0的公共弦所在直线的方程是_____________________.
.
2x-4y+1=0(3).过两圆x2+y2+6x-4=0和x2+y2+6y-28=0的交点
且圆心在直线x-y-4=0上的圆方程是( )
A.x2+y2-x-5y+2=0
B.x2+y2-x-5y-2=0
C.x2+y2-x+7y-32=0
D.x2+y2+x+7y+32=0
跟 踪 训 练C课 堂 小 结1.本节课你收获了什么?(1)知识方面:(2)数学思想方面:判断圆与圆的位置关系的两种方法,以及这两种方法的优劣。求圆与圆相交弦所在直线方程的方法。求圆与圆相交弦的弦长的方法。数形结合的思想,等价转化的思想,类比思想。1.圆A:x2+y2=25和圆B:x2+(y-6)2=1的位 置关系
是 ________
2.圆x2+y2=a(a>0)与x2+y2+6x-8y-11=0相内切,则
实数a的值为________答案:1、外切; 2、1或121拓 展 练 习
