人教版数学必修二 3.1.1直线的倾斜角与斜率(共26张ppt)
文档属性
| 名称 | 人教版数学必修二 3.1.1直线的倾斜角与斜率(共26张ppt) |  | |
| 格式 | zip | ||
| 文件大小 | 727.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教新课标A版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-06 22:35:28 | ||
图片预览






文档简介
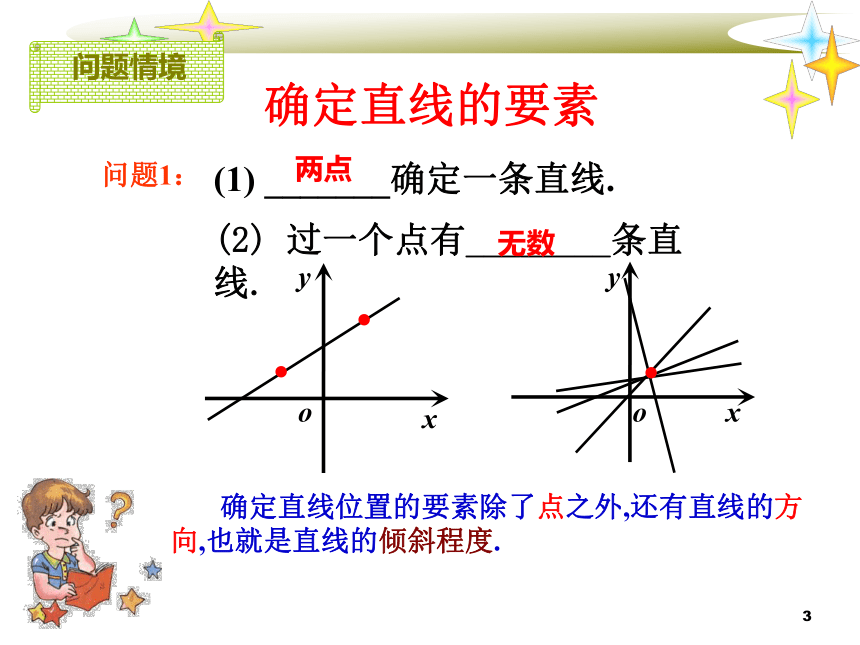
课件26张PPT。3.1.1直线的倾斜角与斜率2问题情境直线—最简单的几何图形飞逝的流星沿不同的方向运动在空中形成美丽的直线3问题情境确定直线的要素问题1:(1) _______确定一条直线.两点(2) 过一个点有________条直线. 无数 确定直线位置的要素除了点之外,还有直线的方向,也就是直线的倾斜程度....问题1:如何确定一条直线在直角坐标
系的位置呢?
从刚才的例子我们看到:只知道一点或者知道直线的方向,直线是不确定的。
两点或一点和方向
问题2:如何表示直线方向(或者倾斜程度呢)?
用角一、直线的倾斜角1、直线倾斜角的定义: 当直线L与X轴相交时,我们取X轴作为基准,X轴正向与直线L向上方向之间所成的角叫做直线的倾斜角 注意: (1)直线向上方向;
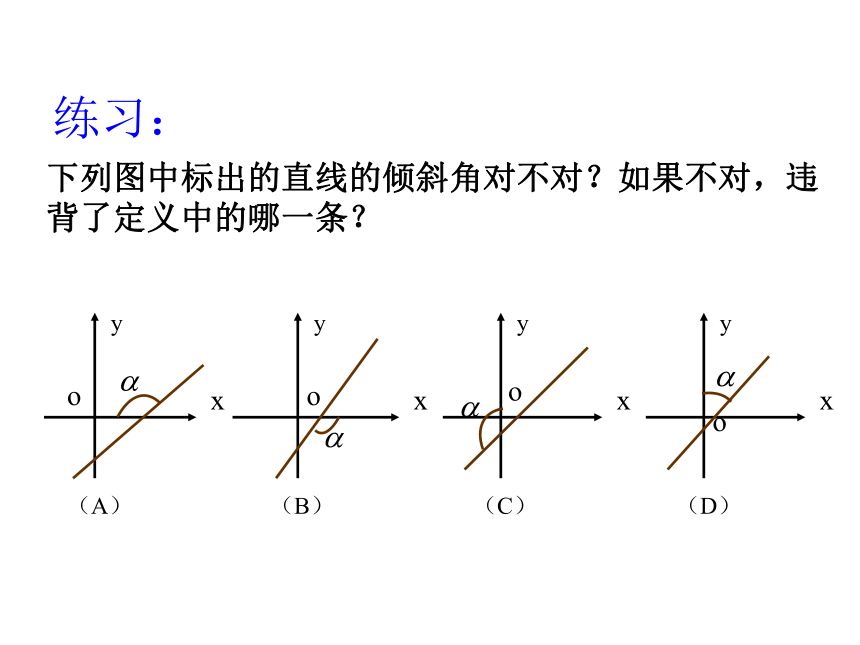
(2)x轴的正方向。练习: 下列图中标出的直线的倾斜角对不对?如果不对,违背了定义中的哪一条?规定:当直线和x轴平行或重合时,
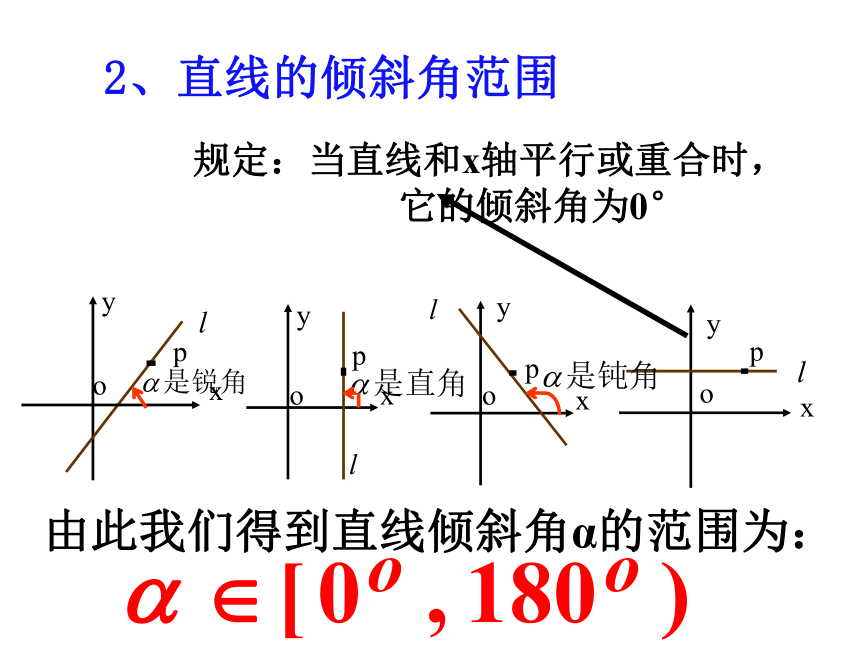
它的倾斜角为0°2、直线的倾斜角范围由此我们得到直线倾斜角α的范围为:想一想你认为下列说法对吗?1、所有的直线都有唯一确定的倾斜
角与它对应。2、每一个倾斜角都对应于唯一的一
条直线。日常生活中,还有没有表示倾斜程度的量?问题 倾斜角不是 90? 的直线,它的倾斜角的正
切值叫做这条直线的斜率,通常用 k 表示,即二、直线的斜率1、直线的斜率定义k=tan ?.练习一
已知直线的倾斜角,求对应的斜率 k :
(1)?=0?; (2)?=30?;
(3)?=135?; (4)?=120?.
判断正误: ①直线的倾斜角为α,则直线的斜率为 ②因为平行于y轴的直线的斜率不存在,所以平
行于y轴的直线的倾斜角不存在③两直线的斜率相等,则它们的倾斜角相等;直线过两点斜率公式的推导探究:如图,当α为锐角时,
能不能构造一个直角三角形去求?锐角 如图,当α为钝角是, 钝角 思考?1、当 的位置对调时, 值又如何呢? 思考?2、当直线平行于x轴,或与x轴重合时,上述公式还适用吗?为什么?成立,因为分子为0,分母不为0,K=0 3、当直线平行于y轴,或与y轴重合时,上述公式还适用吗?为什么?思考?不成立,因为分母为0。2.斜率公式公式的特点:(1) 与两点的顺序无关;(3) 公式表明,直线的斜率可以通过直线上任意两(2) 当x1=x2时,公式不适用,此时α=900点的坐标来表示,而不需要求出直线的倾斜角经过两点 的直线的斜率公式X.pYOX.pYOX.pYOX.pYO(1)(2)(4)(3)ooK>0K<0K不存在K=0 直线AB的斜率直线BC的斜率直线CA的斜率∵ ∴直线CA的倾斜角为锐角∴直线BC的倾斜角为钝角。解: ∵∴直线AB的倾斜角为零度角。∵ 例1三、典型例题例2、在平面直角坐标系中,画出经过原点且斜率分别为1,-1,2和-3的直线 。(1,1)(1,-1)(1,2)(1,-3)例3、求经过A(-2,0), B(-5,3)两点的直线的斜率 变式1、在例3基础上加上点C(m,4)也在直线上,求m。变式2、在例3基础上加上点D(8,6),判断点D是否在直线上。四、当堂检测 1.若直线l向上的方向与y轴正方向成
30o角,则l的倾斜角为 ,
l的斜率为 2.当且仅当m为何值时,经过两点
A(m,3)、B(-m,2m-1)的直线
的倾斜角为60o?五、归纳小结: 1、直线的倾斜角定义及其范围:2、直线的斜率定义:3、斜率k与倾斜角 之间的关系:4、斜率公式:
系的位置呢?
从刚才的例子我们看到:只知道一点或者知道直线的方向,直线是不确定的。
两点或一点和方向
问题2:如何表示直线方向(或者倾斜程度呢)?
用角一、直线的倾斜角1、直线倾斜角的定义: 当直线L与X轴相交时,我们取X轴作为基准,X轴正向与直线L向上方向之间所成的角叫做直线的倾斜角 注意: (1)直线向上方向;
(2)x轴的正方向。练习: 下列图中标出的直线的倾斜角对不对?如果不对,违背了定义中的哪一条?规定:当直线和x轴平行或重合时,
它的倾斜角为0°2、直线的倾斜角范围由此我们得到直线倾斜角α的范围为:想一想你认为下列说法对吗?1、所有的直线都有唯一确定的倾斜
角与它对应。2、每一个倾斜角都对应于唯一的一
条直线。日常生活中,还有没有表示倾斜程度的量?问题 倾斜角不是 90? 的直线,它的倾斜角的正
切值叫做这条直线的斜率,通常用 k 表示,即二、直线的斜率1、直线的斜率定义k=tan ?.练习一
已知直线的倾斜角,求对应的斜率 k :
(1)?=0?; (2)?=30?;
(3)?=135?; (4)?=120?.
判断正误: ①直线的倾斜角为α,则直线的斜率为 ②因为平行于y轴的直线的斜率不存在,所以平
行于y轴的直线的倾斜角不存在③两直线的斜率相等,则它们的倾斜角相等;直线过两点斜率公式的推导探究:如图,当α为锐角时,
能不能构造一个直角三角形去求?锐角 如图,当α为钝角是, 钝角 思考?1、当 的位置对调时, 值又如何呢? 思考?2、当直线平行于x轴,或与x轴重合时,上述公式还适用吗?为什么?成立,因为分子为0,分母不为0,K=0 3、当直线平行于y轴,或与y轴重合时,上述公式还适用吗?为什么?思考?不成立,因为分母为0。2.斜率公式公式的特点:(1) 与两点的顺序无关;(3) 公式表明,直线的斜率可以通过直线上任意两(2) 当x1=x2时,公式不适用,此时α=900点的坐标来表示,而不需要求出直线的倾斜角经过两点 的直线的斜率公式X.pYOX.pYOX.pYOX.pYO(1)(2)(4)(3)ooK>0K<0K不存在K=0 直线AB的斜率直线BC的斜率直线CA的斜率∵ ∴直线CA的倾斜角为锐角∴直线BC的倾斜角为钝角。解: ∵∴直线AB的倾斜角为零度角。∵ 例1三、典型例题例2、在平面直角坐标系中,画出经过原点且斜率分别为1,-1,2和-3的直线 。(1,1)(1,-1)(1,2)(1,-3)例3、求经过A(-2,0), B(-5,3)两点的直线的斜率 变式1、在例3基础上加上点C(m,4)也在直线上,求m。变式2、在例3基础上加上点D(8,6),判断点D是否在直线上。四、当堂检测 1.若直线l向上的方向与y轴正方向成
30o角,则l的倾斜角为 ,
l的斜率为 2.当且仅当m为何值时,经过两点
A(m,3)、B(-m,2m-1)的直线
的倾斜角为60o?五、归纳小结: 1、直线的倾斜角定义及其范围:2、直线的斜率定义:3、斜率k与倾斜角 之间的关系:4、斜率公式:
