沪教版(五四学制)六年级数学上册4.1 圆的周长(1) 课件(共32张)
文档属性
| 名称 | 沪教版(五四学制)六年级数学上册4.1 圆的周长(1) 课件(共32张) |  | |
| 格式 | zip | ||
| 文件大小 | 1.8MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-04 09:57:19 | ||
图片预览



文档简介
(共32张PPT)
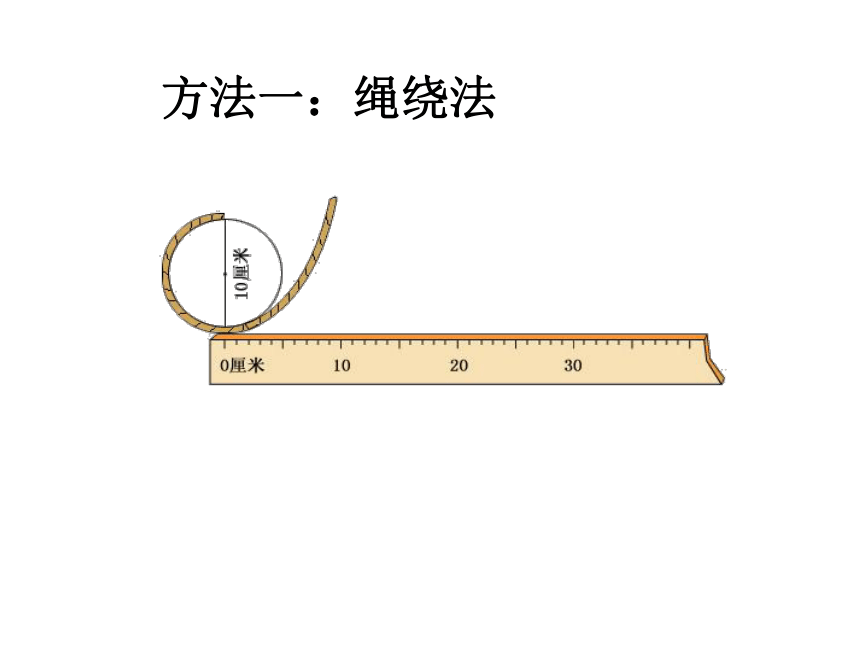
思考:A、B两只蚂蚁分别沿边长为3米的正方形和
直径为3米的圆形爬行,如果它们同时同速出发,
那么谁先回到出发点?
(关键是比较什么?求什么?)
a=3米
d=3米
A
B
想一想:什么叫圆的周长
围成圆的曲线的长叫做圆的周长。
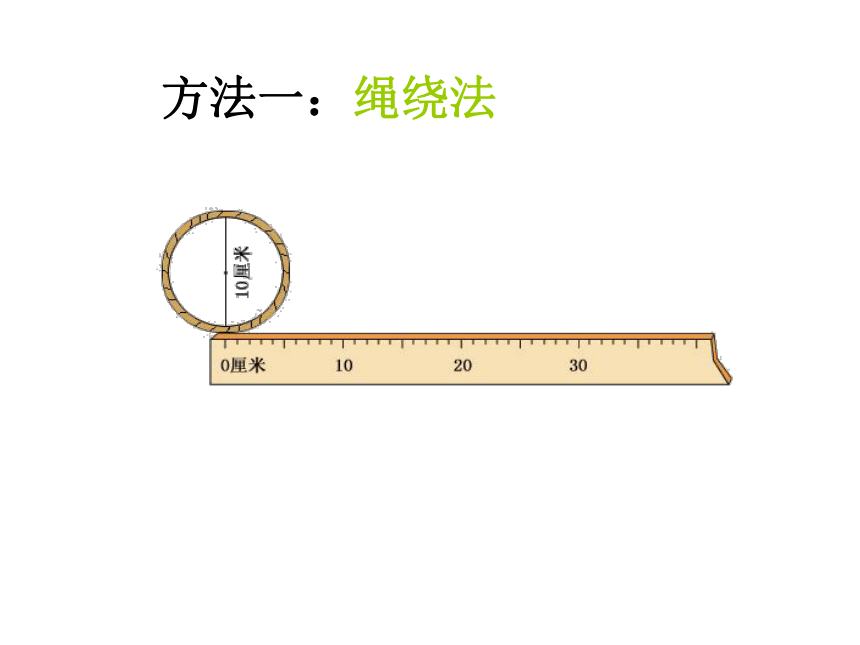
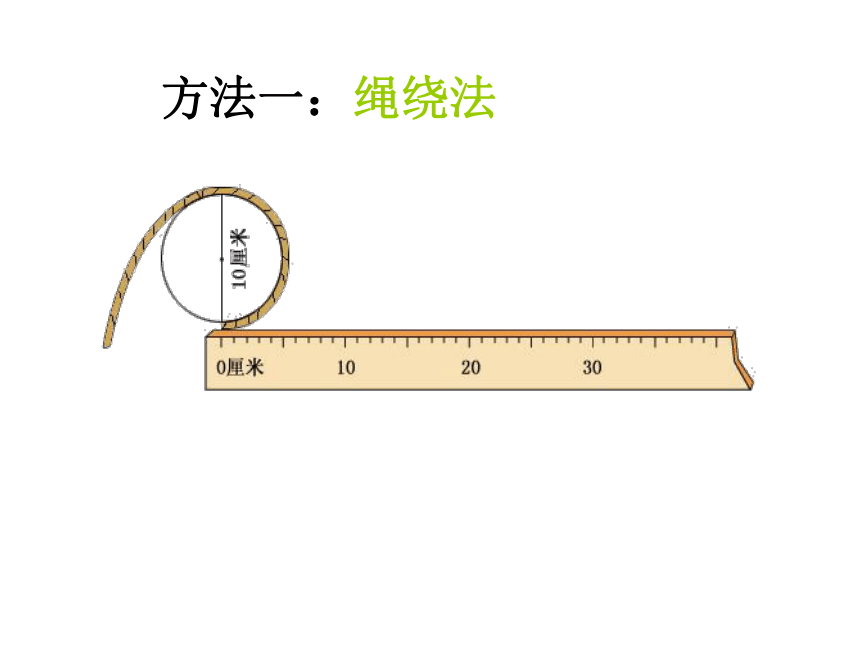
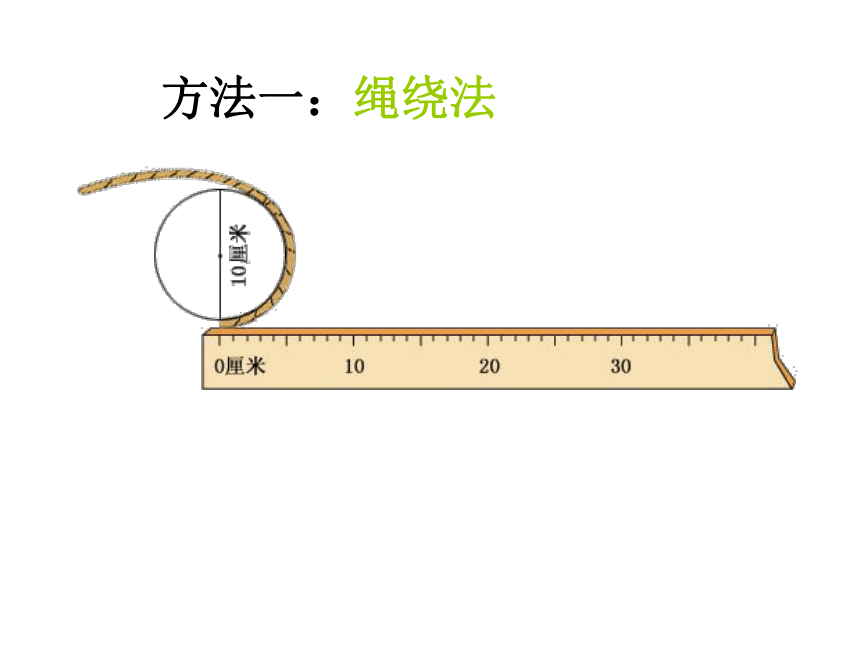
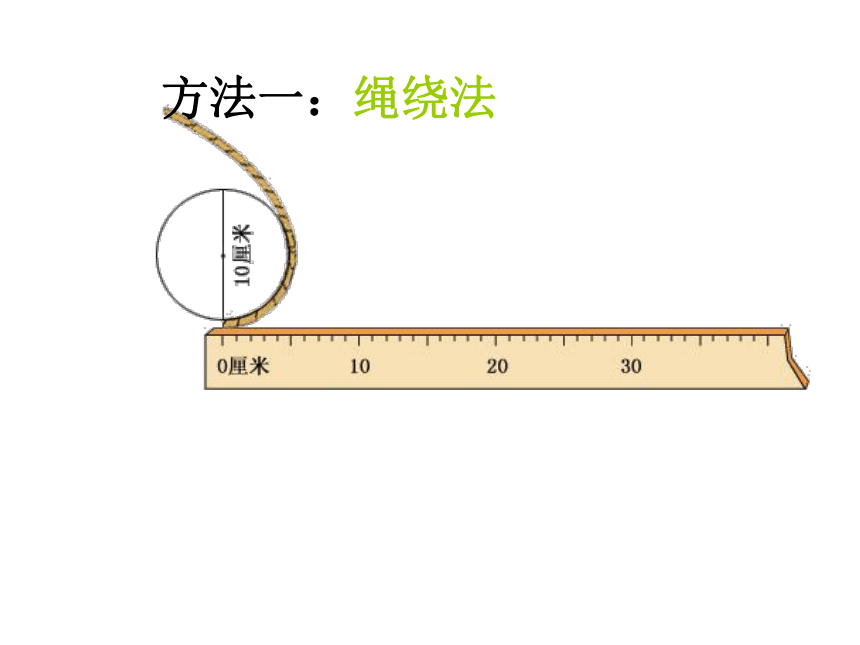
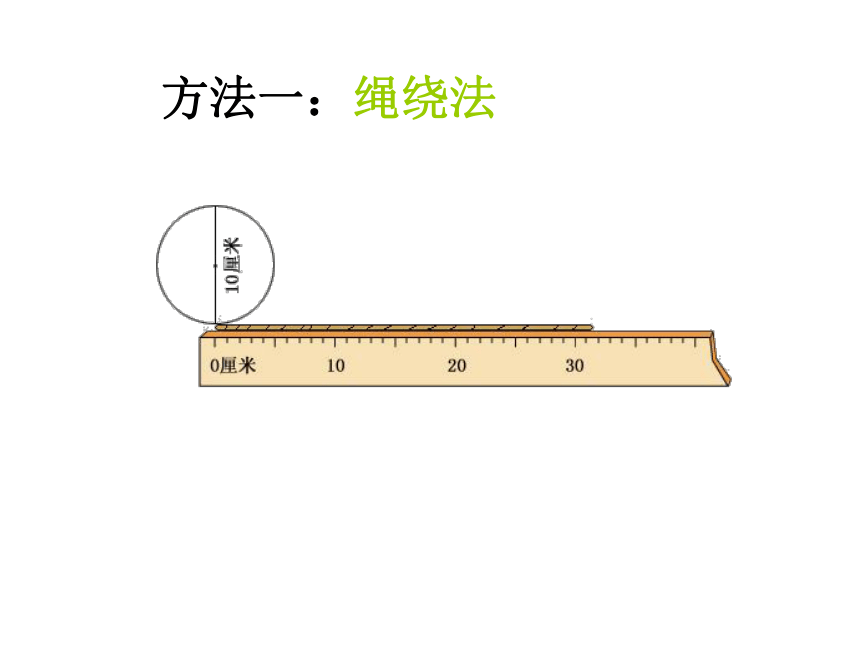
方法一:绳绕法
方法一:绳绕法
方法一:绳绕法
方法一:绳绕法
方法一:绳绕法
方法一:绳绕法
0cm
10
20
30
40
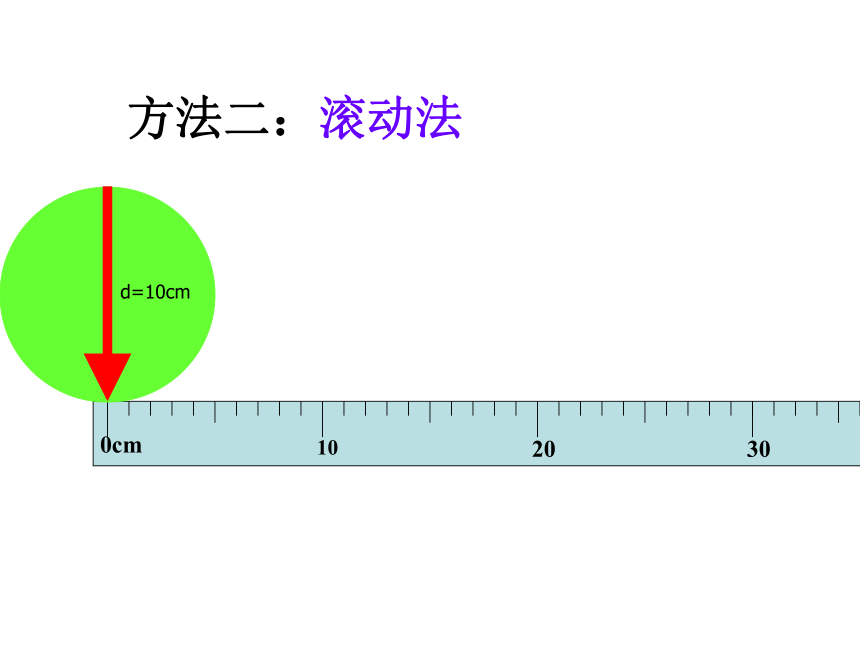
方法二:滚动法
d=10cm
10
20
30
40
方法二:滚动法
d=10cm
0cm
10
20
30
40
方法二:滚动法
d=10cm
0cm
10
20
30
40
方法二:滚动法
d=10cm
0cm
10
20
30
40
方法二:滚动法
d=10cm
0cm
10
20
30
40
方法二:滚动法
d=10cm
0cm
10
20
30
40
方法二:滚动法
d=10cm
0cm
10
20
30
40
方法二:滚动法
d=10cm
0cm
10
20
30
40
方法二:滚动法
d=10cm
0cm
圆向右滚动一周,量它的长度。
如何测量圆的直径?
1、分小组测量圆的周长和直径
周
长
C(毫米)
直
径
d(毫米)
C与d的比值(保留两位小数)
2、填表:
自己动手量一量
你发现了什么?
圆的周长除以直径的商是一个固定的数。我们把它叫做圆周率,用字母π
(读作pài)表示。
π=3.141592653
π
≈3.14
约2000年前,中国的古代数学著作《周髀(bì)算经》中就有了“周三径一”的说法,意思是指圆的周长是它的直径的3倍。
大约1500年前,中国有一位伟大的数学家和天文学家祖冲之,他计算出圆周率应在3.1415926和3.1415927之间,成为世界上第一个把圆周率的值精确到7位小数的人。他的这项伟大成就比国外数学家得出这样精确数值的时间,至少要早1000年。
1967年,这个倍数被算到小数点后50万位,现在随着计算机的发展π精确估计可以达到小数位的几十亿位,但仍然未算完。后来人们进一步证明了π既不是整数,也不是分数,而是一个无限不循环小数,要算出π的准确值是不可能的。
π=3.1415926
535
897
93238462643383279502884197169399375105820974944592307816406286208998628034825342117067982148086513282306647093844609550582231725359408128481117450284102701938521105559644622948954930389644288109756659334461284756482337867831652712019091456485669234603486……
判断辨析
1、π=3.14
(
)
2、只要知道圆的直径或者半径,就可以知道圆的周长(
)
3、大圆的圆周率比小圆的圆周率大。
(
)
×
√
×
解决问题:A、B两只蚂蚁分别沿边长为3米的正方形
和直径为3米的圆形爬行,如果它们同时同速出发,
那么谁先回到出发点?
(本章中,无特殊说明时,
π取3.14)
a=3米
d=3米
A
B
汽车轮胎的半径是0.3米,它滚动1圈前进多少米?(π取3.14)
﹋
﹋
例题2
一颗卫星围绕地球飞行,飞行轨道
近似为圆形,已知卫星距离地球表面500
千米,飞行了14圈,问卫星一共飞行了
多少千米?(地球的半径约为6400千米)
2.圆的周长公式:
小
结
d
r
1.圆周率
是个无限不循环小数.
大圆的周长和两个小圆的周长之和,谁长呢?
大圆:d=2+4=6(米)
C=3.14×6
=18.84(米)
小圆:C=3.14×2+3.14×4
=6.28+12.56
=18.84(米)
答:大圆的周长和两
个小圆的周长之和相等。
大圆的周长和三个小圆的周长之和,谁长呢?
思考:A、B两只蚂蚁分别沿边长为3米的正方形和
直径为3米的圆形爬行,如果它们同时同速出发,
那么谁先回到出发点?
(关键是比较什么?求什么?)
a=3米
d=3米
A
B
想一想:什么叫圆的周长
围成圆的曲线的长叫做圆的周长。
方法一:绳绕法
方法一:绳绕法
方法一:绳绕法
方法一:绳绕法
方法一:绳绕法
方法一:绳绕法
0cm
10
20
30
40
方法二:滚动法
d=10cm
10
20
30
40
方法二:滚动法
d=10cm
0cm
10
20
30
40
方法二:滚动法
d=10cm
0cm
10
20
30
40
方法二:滚动法
d=10cm
0cm
10
20
30
40
方法二:滚动法
d=10cm
0cm
10
20
30
40
方法二:滚动法
d=10cm
0cm
10
20
30
40
方法二:滚动法
d=10cm
0cm
10
20
30
40
方法二:滚动法
d=10cm
0cm
10
20
30
40
方法二:滚动法
d=10cm
0cm
圆向右滚动一周,量它的长度。
如何测量圆的直径?
1、分小组测量圆的周长和直径
周
长
C(毫米)
直
径
d(毫米)
C与d的比值(保留两位小数)
2、填表:
自己动手量一量
你发现了什么?
圆的周长除以直径的商是一个固定的数。我们把它叫做圆周率,用字母π
(读作pài)表示。
π=3.141592653
π
≈3.14
约2000年前,中国的古代数学著作《周髀(bì)算经》中就有了“周三径一”的说法,意思是指圆的周长是它的直径的3倍。
大约1500年前,中国有一位伟大的数学家和天文学家祖冲之,他计算出圆周率应在3.1415926和3.1415927之间,成为世界上第一个把圆周率的值精确到7位小数的人。他的这项伟大成就比国外数学家得出这样精确数值的时间,至少要早1000年。
1967年,这个倍数被算到小数点后50万位,现在随着计算机的发展π精确估计可以达到小数位的几十亿位,但仍然未算完。后来人们进一步证明了π既不是整数,也不是分数,而是一个无限不循环小数,要算出π的准确值是不可能的。
π=3.1415926
535
897
93238462643383279502884197169399375105820974944592307816406286208998628034825342117067982148086513282306647093844609550582231725359408128481117450284102701938521105559644622948954930389644288109756659334461284756482337867831652712019091456485669234603486……
判断辨析
1、π=3.14
(
)
2、只要知道圆的直径或者半径,就可以知道圆的周长(
)
3、大圆的圆周率比小圆的圆周率大。
(
)
×
√
×
解决问题:A、B两只蚂蚁分别沿边长为3米的正方形
和直径为3米的圆形爬行,如果它们同时同速出发,
那么谁先回到出发点?
(本章中,无特殊说明时,
π取3.14)
a=3米
d=3米
A
B
汽车轮胎的半径是0.3米,它滚动1圈前进多少米?(π取3.14)
﹋
﹋
例题2
一颗卫星围绕地球飞行,飞行轨道
近似为圆形,已知卫星距离地球表面500
千米,飞行了14圈,问卫星一共飞行了
多少千米?(地球的半径约为6400千米)
2.圆的周长公式:
小
结
d
r
1.圆周率
是个无限不循环小数.
大圆的周长和两个小圆的周长之和,谁长呢?
大圆:d=2+4=6(米)
C=3.14×6
=18.84(米)
小圆:C=3.14×2+3.14×4
=6.28+12.56
=18.84(米)
答:大圆的周长和两
个小圆的周长之和相等。
大圆的周长和三个小圆的周长之和,谁长呢?
