沪教版(五四学制)六上:4.1 圆的周长 课件(23张PPT)
文档属性
| 名称 | 沪教版(五四学制)六上:4.1 圆的周长 课件(23张PPT) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.7MB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-04 00:00:00 | ||
图片预览








文档简介
(共23张PPT)
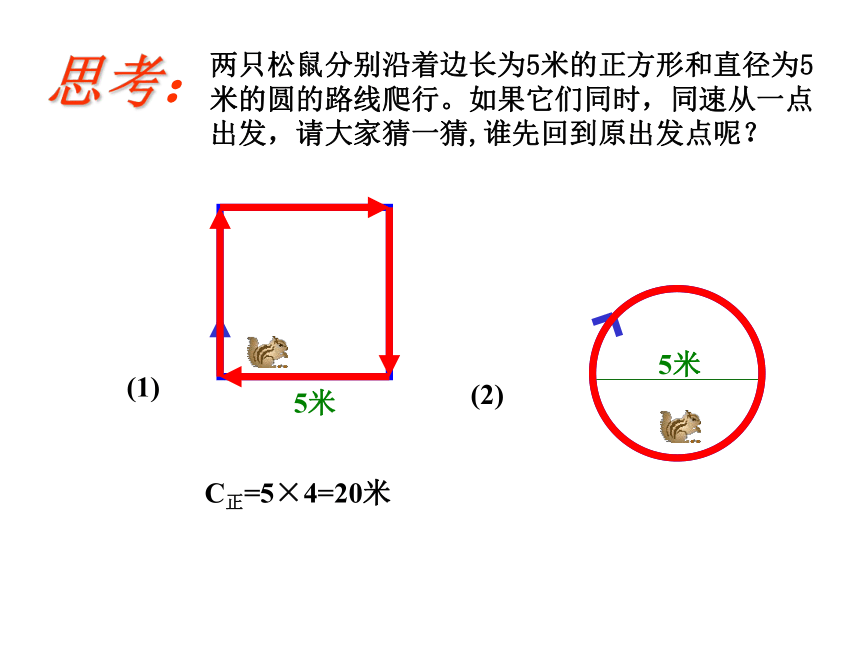
两只松鼠分别沿着边长为5米的正方形和直径为5米的圆的路线爬行。如果它们同时,同速从一点出发,请大家猜一猜,谁先回到原出发点呢?
思考:
5米
C正=5×4=20米
(2)
(1)
5米
想一想,议一议,用手中的线,刻度尺等工具,怎样测量出圆的周长,看谁的办法多。
实验操作
实验准备:有刻度的直尺,细绳,圆形物体。
实验报告:
物体名称
直径(
cm)
周长(cm)
圆1
圆2
圆3
圆4
周长与直径的比值(精确0.01)
约2000年前,中国古代数学著作《周髀算经》中就有周三径一的说法,意思是说圆的周长约是直径的三倍.约1500年前,我国古代数学家祖冲之,就精密地计算出圆周率的值在3.1415926和3.1415927之间,比欧洲早1000多年,是当时世界上算得最精确的圆周率的值,
π是个无限不循环小数.
π
所以圆的周长=直径×圆周率
C=
πd
C=2πr
因为直径=半径的2倍
所以圆的周长=半径×2
×圆周率
结论:圆的周长是直径的三倍多一些,三倍多一些可以用圆周率π来表示.
π≈3.14
两只松鼠分别沿着边长为5米的正方形和直径为5米的圆的路线爬行。如果它们同时,同速从一点出发,请大家猜一猜,谁先回到原出发点呢?
思考:
5米
C正=5×4=20米
(2)
(1)
5米
C圆=3.14
×5=15.7米
因为15.7米小于20米,所以松鼠(2)先回到原出发点.
填空,并熟记这些常见数据
(1)已知圆的直径为1cm,则这个圆的周长为
cm;
(2)已知圆的半径为1cm,则这个圆的周长为
cm;
(3)已知圆的直径为3cm,则这个圆的周长为
cm;
(4)已知圆的半径为2cm,则这个圆的周长为
cm;
3.14
6.28
9.42
12.56
(5)已知圆的周长为18.84cm,则这个圆的半径为
cm;
3
(6)已知圆的周长为12.56cm,则这个圆的直径为
cm;
4
(二)填空:
1.甲圆直径6cm乙圆直径2dm,则这两个圆的圆周率大小关系是
。
2.
如果知道了圆的
就可以计算圆的周长。
相等
直径或半径
3.闹钟的秒针长5cm,那么秒针尖端转动一周的周长是
2×3.14×5=31.4cm
10分钟后,秒针转动的长度是
cm
31.4×10=314
1.一辆自行车直线行驶,车轮半径是0.33米,车轮滚动一周,自行车前进约多少米 (结果保留两位小数)
解:r=0.33
c=2πr
=2×3.14×0.33
=2.0724
≈2.07(米)
答:车轮滚动一周,自行车前进约2.07米
练习:
1.一张玉莲的叶子近似于一个圆,它的直径约是0.95米,这张叶子的周长约是多少米?(结果保留两位小数)
答:这张叶子的周长约是2.98米
解:
d=0.95
C=πd
=3.14×0.95
=2.983
≈2.98(米)
例题2
一颗卫星围绕地球飞行,飞行轨道近似为圆形,已知卫星距离地球表面500千米,飞行了14圈,问卫星一共飞行了多少千米?(地球的半径约为6400千米)
6400
6900
解:R轨=500+6400
=6900
C轨=2π
R轨
=2×3.14×6900
=43332
14C轨=43332×14
=606648(千米)
答:卫星围绕
地球一共飞行了约606648千米
练习2
如图,圆环的外圆周长C1=250cm,内圆周长C2=150cm,求圆环的宽度d(结果精确到0.1cm)。
r2
r1
d
O
解:已知C=2πr=2×3.14×r=6.28r
r
=
C÷6.28
d
=
r1-r2
=C1÷6.28-C2÷6.28
=(C1-C2)
÷6.28
=(250-150)
÷6.28
≈15.9(cm)
答:圆环的宽度约是15.9cm
如图是一个由半圆和一条直径所组成的图形,求这个图形的周长,小明,小丽,小杰谁说得对?为什么?
小明
小丽
小杰
o
思考:
5
通过这节课的学习,你有什么收获
(1)圆周率的意义:任何圆的周长和直径的
比值是3倍多一点,是一个固定的数,我们把这个比值叫圆周率,用字母π表示,
(2)圆周长=直径×圆周率
C=
πd或
2
πr
谢
谢
两只松鼠分别沿着边长为5米的正方形和直径为5米的圆的路线爬行。如果它们同时,同速从一点出发,请大家猜一猜,谁先回到原出发点呢?
思考:
5米
C正=5×4=20米
(2)
(1)
5米
想一想,议一议,用手中的线,刻度尺等工具,怎样测量出圆的周长,看谁的办法多。
实验操作
实验准备:有刻度的直尺,细绳,圆形物体。
实验报告:
物体名称
直径(
cm)
周长(cm)
圆1
圆2
圆3
圆4
周长与直径的比值(精确0.01)
约2000年前,中国古代数学著作《周髀算经》中就有周三径一的说法,意思是说圆的周长约是直径的三倍.约1500年前,我国古代数学家祖冲之,就精密地计算出圆周率的值在3.1415926和3.1415927之间,比欧洲早1000多年,是当时世界上算得最精确的圆周率的值,
π是个无限不循环小数.
π
所以圆的周长=直径×圆周率
C=
πd
C=2πr
因为直径=半径的2倍
所以圆的周长=半径×2
×圆周率
结论:圆的周长是直径的三倍多一些,三倍多一些可以用圆周率π来表示.
π≈3.14
两只松鼠分别沿着边长为5米的正方形和直径为5米的圆的路线爬行。如果它们同时,同速从一点出发,请大家猜一猜,谁先回到原出发点呢?
思考:
5米
C正=5×4=20米
(2)
(1)
5米
C圆=3.14
×5=15.7米
因为15.7米小于20米,所以松鼠(2)先回到原出发点.
填空,并熟记这些常见数据
(1)已知圆的直径为1cm,则这个圆的周长为
cm;
(2)已知圆的半径为1cm,则这个圆的周长为
cm;
(3)已知圆的直径为3cm,则这个圆的周长为
cm;
(4)已知圆的半径为2cm,则这个圆的周长为
cm;
3.14
6.28
9.42
12.56
(5)已知圆的周长为18.84cm,则这个圆的半径为
cm;
3
(6)已知圆的周长为12.56cm,则这个圆的直径为
cm;
4
(二)填空:
1.甲圆直径6cm乙圆直径2dm,则这两个圆的圆周率大小关系是
。
2.
如果知道了圆的
就可以计算圆的周长。
相等
直径或半径
3.闹钟的秒针长5cm,那么秒针尖端转动一周的周长是
2×3.14×5=31.4cm
10分钟后,秒针转动的长度是
cm
31.4×10=314
1.一辆自行车直线行驶,车轮半径是0.33米,车轮滚动一周,自行车前进约多少米 (结果保留两位小数)
解:r=0.33
c=2πr
=2×3.14×0.33
=2.0724
≈2.07(米)
答:车轮滚动一周,自行车前进约2.07米
练习:
1.一张玉莲的叶子近似于一个圆,它的直径约是0.95米,这张叶子的周长约是多少米?(结果保留两位小数)
答:这张叶子的周长约是2.98米
解:
d=0.95
C=πd
=3.14×0.95
=2.983
≈2.98(米)
例题2
一颗卫星围绕地球飞行,飞行轨道近似为圆形,已知卫星距离地球表面500千米,飞行了14圈,问卫星一共飞行了多少千米?(地球的半径约为6400千米)
6400
6900
解:R轨=500+6400
=6900
C轨=2π
R轨
=2×3.14×6900
=43332
14C轨=43332×14
=606648(千米)
答:卫星围绕
地球一共飞行了约606648千米
练习2
如图,圆环的外圆周长C1=250cm,内圆周长C2=150cm,求圆环的宽度d(结果精确到0.1cm)。
r2
r1
d
O
解:已知C=2πr=2×3.14×r=6.28r
r
=
C÷6.28
d
=
r1-r2
=C1÷6.28-C2÷6.28
=(C1-C2)
÷6.28
=(250-150)
÷6.28
≈15.9(cm)
答:圆环的宽度约是15.9cm
如图是一个由半圆和一条直径所组成的图形,求这个图形的周长,小明,小丽,小杰谁说得对?为什么?
小明
小丽
小杰
o
思考:
5
通过这节课的学习,你有什么收获
(1)圆周率的意义:任何圆的周长和直径的
比值是3倍多一点,是一个固定的数,我们把这个比值叫圆周率,用字母π表示,
(2)圆周长=直径×圆周率
C=
πd或
2
πr
谢
谢
