五年级上册数学试题-奥数:周期问题(A)全国通用(含答案)
文档属性
| 名称 | 五年级上册数学试题-奥数:周期问题(A)全国通用(含答案) |  | |
| 格式 | zip | ||
| 文件大小 | 179.2KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 通用版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-03 14:10:15 | ||
图片预览


文档简介
八 周期性问题(A)
年级 班 姓名 得分
一、填空题
1. 某年的二月份有五个星期日,这年六月一日是星期_____.
2. 1989年12月5日是星期二,那么再过十年的12月5日是星期_____.
3. 按下面摆法摆80个三角形,有_____个白色的.
……
4.节日的校园内挂起了一盏盏小电灯,小明看出每两个白灯之间有红、黄、绿各一盏彩灯.也就是说,从第一盏白灯起,每一盏白灯后面都紧接着有3盏彩灯,小明想第73盏灯是_____灯.
5. 时针现在表示的时间是14时正,那么分针旋转1991周后,时针表示的时间是_____.
6. 把自然数1,2,3,4,5……如表依次排列成5列,那么数“1992”在_____列.
第一列
第二列
第三列
第四列
第五列
1
2
3
4
5
9
8
7
6
10
11
12
13
14
18
17
16
15
…
…
…
…
…
…
…
…
…
7. 把分数化成小数后,小数点第110位上的数字是_____.
8. 循环小数与.这两个循环小数在小数点后第_____位,首次同时出现在该位中的数字都是7.
9. 一串数: 1,9,9,1,4,1, 4,1,9,9,1,4,1,4,1,9,9,1,4,……共有1991个数.
(1)其中共有_____个1,_____个9_____个4;
(2)这些数字的总和是_____.
10. 所得积末位数是_____.
二、解答题
11. 紧接着1989后面一串数字,写下的每个数字都是它前面两个数字的乘积的个位数.例如89=72,在9后面写2,92=18,在2后面写8,……得到一串数字:
1 9 8 9 2 8 6……
这串数字从1开始往右数,第1989个数字是什么?
12. 1991个1990相乘所得的积与1990个1991相乘所得的积,再相加的和末两位数是多少?
13. 设,那么n的末两位数字是多少?
14.在一根长100厘米的木棍上,自左至右每隔6厘米染一个红点,同时自右至左每隔5厘米也染一个红点,然后沿红点处将木棍逐段锯开,那么长度是1厘米的短木棍有多少根?
八 周期性问题(B)
年级 班 姓名 得分
一、填空题
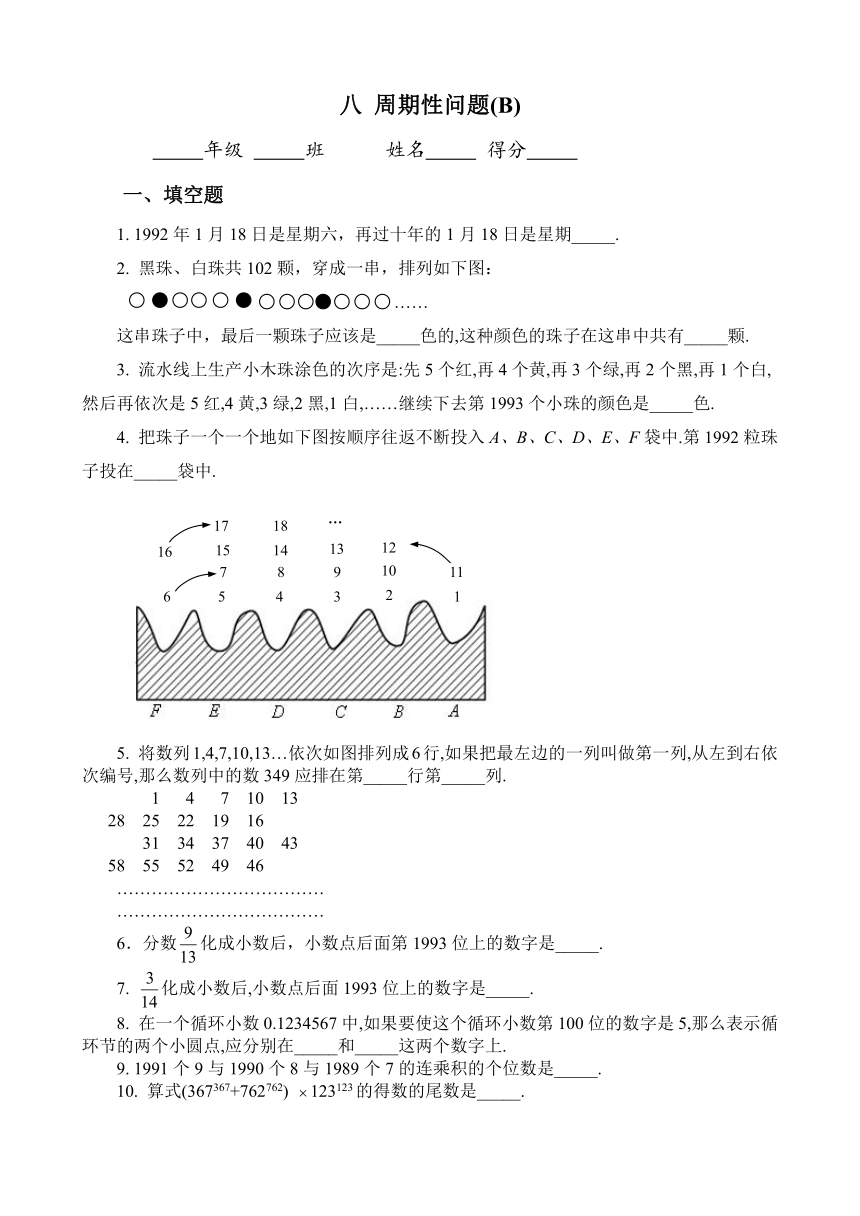
1. 1992年1月18日是星期六,再过十年的1月18日是星期_____.
2. 黑珠、白珠共102颗,穿成一串,排列如下图:
……
这串珠子中,最后一颗珠子应该是_____色的,这种颜色的珠子在这串中共有_____颗.
3. 流水线上生产小木珠涂色的次序是:先5个红,再4个黄,再3个绿,再2个黑,再1个白,然后再依次是5红,4黄,3绿,2黑,1白,……继续下去第1993个小珠的颜色是_____色.
4. 把珠子一个一个地如下图按顺序往返不断投入A、B、C、D、E、F袋中.第1992粒珠子投在_____袋中.
5. 将数列1,4,7,10,13…依次如图排列成6行,如果把最左边的一列叫做第一列,从左到右依次编号,那么数列中的数349应排在第_____行第_____列.
1 4 7 10 13
28 25 22 19 16
31 34 37 40 43
58 55 52 49 46
………………………………
………………………………
6.分数化成小数后,小数点后面第1993位上的数字是_____.
7. 化成小数后,小数点后面1993位上的数字是_____.
8. 在一个循环小数0.1234567中,如果要使这个循环小数第100位的数字是5,那么表示循环节的两个小圆点,应分别在_____和_____这两个数字上.
9. 1991个9与1990个8与1989个7的连乘积的个位数是_____.
10. 算式(367367+762762) 123123的得数的尾数是_____.
二、解答题
11. 乘积1234……19901991是一个多位数,而且末尾有许多零,从右到左第一个不等于零的数是多少?
12.有串自然数,已知第一个数与第二个数互质,而且第一个数的恰好是第二个数的,从第三个数开始,每个数字正好是前两个数的和,问这串数的第1991个数被3除所得的余数是几?
共产党好共产党好共产党好……
社会主义好社会主义好社会主义好……
上表中,将每列上下两个字组成一组,例如第一组为(共社),第二组为(产会),那么第340组是_____.
14. 甲、乙二人对一根3米长的木棍涂色.首先,甲从木棍端点开始涂黑5厘米,间隔5厘米不涂色,接着再涂黑5厘米,这样交替做到底.然后,乙从木棍同一端点开始留出6厘米不涂色,接着涂黑6厘米,再间隔6厘米不涂色,交替做到底.最后,木棍上没有被涂黑部分的长度总和为_____厘米.
———————————————答 案——————————————————————
1. 二
因为74=28,由某年二月份有五个星期日,所以这年二月份应是29天,且2月1日与2月29日均为星期日,3月1日是星期一,所以从这年3月1日起到这年6月1日共经过了
31+30+31+1=93(天).
因为93(7=13…2,所以这年6月1日是星期二.
2. 日
依题意知,这十年中1992年、1996年都是闰年,因此,这十年之中共有
36510+2=3652(天)
因为(3652+1)7=521…6,所以再过十年的12月5日是星期日.
[注]上述两题(题1—题2)都是推断若干天、若干月或若干年后某一天为星期几,解答这类问题主要依据每周为七天循环的规律,运用周期性解答.在计算天数时,要根据“四年一闰,整百不闰,四百年才又一闰”的规定,即公历年份不是整百数时,只要是4的倍数就是闰年,公历年数为整百数时,必须是400的倍数才是闰年.
3. 39
从图中可以看出,三角形按“二黑二白一黑一白”的规律重复排列,也就是这一排列的周期为6,并且每一周期有3个白色三角形.
因为806=13…2,而第十四期中前两个三角形都是黑色的,所以共有白色三角形133=39(个).
4. 白
依题意知,电灯的安装排列如下:
白,红,黄,绿,白,红,黄,绿,白,……这一排列是按“白,红,黄,绿”交替循环出现的,也就是这一排列的周期为4.
由734=18…1,可知第73盏灯是白灯.
5. 13时.
分针旋转一周为1小时,旋转1991周为1991小时.一天24小时,199124=82…23,1991小时共82天又23小时.现在是14时正,经过82天仍然是14时正,再过23小时,正好是13时.
[注]在圆面上,沿着圆周把1到12的整数等距排成一个圈,再加上一根长针和一根短针,就组成了我们天天见到的钟面.钟面虽然是那么的简单平常,但在钟面上却包含着十分有趣的数学问题,周期现象就是其中的一个重要方面.
6. 3
仔细观察题中数表.
1 2 3 4 5 (奇数排)
第一组
8 7 6 (偶数排)
10 11 12 13 14 (奇数排)
第二组
18 17 16 15 (偶数排)
19 20 21 22 23 (奇数排)
第三组
27 26 25 24 (偶数排)
可发现规律如下:
(1)连续自然数按每组9个数,且奇数排自左往右五个数,偶数排自右往左四个数的规律循环排列;
(2)观察第二组,第三组,发现奇数排的数如果用9除有如下规律:第1列用9除余数为1,第2列用9除余数为2,…,第5列用9除余数为5.
(3)109=1…1,10在1+1组,第1列
199=2…1,19在2+1组,第1列
因为19929=221…3,所以1992应排列在(221+1)=222组中奇数排第3列数的位置上.
7. 7
=0.57142857……
它的循环周期是6,具体地六个数依次是
5,7,1,4,2,8
1106=18…2
因为余2,第110个数字是上面列出的六个数中的第2个,就是7.
8. 35
因为0.1992517的循环周期是7,0.34567的循环周期为5,又5和7的最小公倍数是35,所以两个循环小数在小数点后第35位,首次同时出现在该位上的数字都是7.
9. 853,570,568,8255.
不难看出,这串数每7个数即1,9,9,1,4,1,4为一个循环,即周期为7,且每个周期中有3个1,2个9,2个4.因为1991(7=284…3,所以这串数中有284个周期,加上第285个周期中的前三个数1,9,9.其中1的个数是:3(284+1=853(个),9的个数是2(284+2=570(个),4的个数是2(284=568(个).这些数字的总和为
1(853+9(570+4(568=8255.
10. 9
先找出积的末位数的变化规律:
71末位数为7,72末位数为9,73末位数为3, 74末位数1;75=74+1末位数为7,76=74+2末位数为9,77=74+3末位数为3,78=末位数为1……
由此可见,积的末位依次为7,9,3,1,7,9,3,1……,以4为周期循环出现.
因为504=12…2,即750=,所以750与72末位数相同,也就是积的末位数是9.
11. 依照题述规则多写几个数字:
1989286884286884……
可见1989后面的数总是不断循环重复出现286884,每6个一组,即循环周期为6.因为(1989-4)6=330…5,所以所求数字是8.
12. 1991个1990相乘所得的积末两位是0,我们只需考察1990个1991相乘的积末两位数即可.1个1991末两位数是91,2个1991相乘的积末两位数是81,3个1991相乘的积末两位数是71,4个至10个1991相乘的积的末两位数分别是61,51,41,31,21,11,01,11个1991相乘积的末两位数字是91,……,由此可见,每10个1991相乘的末两位数字重复出现,即周期为10.因为199010=199,所以1990个1991相乘积的末两位数是01,即所求结果是01.
13. n是1991个2的连乘积,可记为n=21991,首先从2的较低次幂入手寻找规律,列表如下:
n
n的十位数字
n的个位数字
n
n的十位数字
n的个位数字
21
0
2
212
9
6
22
0
4
213
9
2
23
0
8
214
8
4
24
1
6
215
6
8
25
3
2
216
3
6
26
6
4
217
7
2
27
2
8
218
4
4
28
5
6
219
8
8
29
1
2
220
7
6
210
2
4
221
5
2
211
4
8
222
0
4
观察上表,容易发现自22开始每隔20个2的连乘积,末两位数字就重复出现,周期为20.因为199020=99…10,所以21991与211的末两位数字相同,由上表知211的十位数字是4,个位数字是8.所以,n的末两位数字是48.
14. 因为100能被5整除,所以自右至左染色也就是自左至右染色.于是我们可以看作是从同一端点染色.
6与5的最小公倍数是30,即在30厘米的地方,同时染上红色,这样染色就会出现循环,每一周的长度是30厘米,如下图所示.
由图示可知长1厘米的短木棍,每一周期中有两段,如第1周期中,6-5=1,55-64=1.剩余10厘米中有一段.所以锯开后长1厘米的短木棍共有7段.综合算式为:
2[(100-10)30]+1
=23+1
=7(段)
[注]解决这一问题的关键是根据整除性把自右向左每隔5厘米的染色,转化为自左向右的染色,便于利用最小公倍数发现周期现象,化难为易.
———————————————答 案——————————————————————
1. 五
在这十年中有3个闰年,所以这10年的总天数是36510+3,365被7除余1,所以总天数被7除的余数是(13-7=)6,因此10年后的1月18日是星期五.
2. 黑,26
根据图示可知,若去掉第一颗白珠后它们的排列是按“一黑三色”交替循环出现的,也就是这一排列的周期为4.
由(102-1)4=25…1,可知循环25个周期,最后一颗珠子是黑色的.黑色珠子共有
125+1=26(颗).
3. 黑
小木球是依次按5红,4黄,3绿,2黑和1白的规律涂色的,把它看成周期性问题,每个周期为15.
由199315=132…13知,第1993个小球是第133周期中的第13个,按规律涂色应该是黑色,所以第1993个小球的颜色是黑色.
4. B
通过观察可以发现,第11次到第20次投进的袋子依次与第1次到第10次投进的袋子相同,即当投的次数被10除余1,2,3,…,8,9,0,分别投进A,B,C,……D,C,B袋中,1992被10除余2,所以第1992粒珠子投在B袋中.
5. 24,2
这个数列从第2项起,每一项都比前一项多3,(349-1)3+1=117,所以349是这列数中的第117个数.
从排列可以看出,每两排为一个周期,每一周期有10个数.
因为11710=11…7,所以数“349”是第11个周期的第7个数,也就是在第24行第2列.
6. 6
=
它的循环周期是6,因为1993=6332+1,所以化成小数后,其小数点后面第1993位上的数字是6.
7. 7
=
它的循环周期是6,因为(1993-1)6=332,则循环节“142857”恰好重复出现332次.所以小数点后面第1993位上的数字是7.
8. 3,7
表示循环小数的两个小圆点中,后一个小圆点显然应加在7的上面,且数字“5”肯定包含在循环节中,设前一个小圆点加在“5”的上面,这时循环周期是3,(100-4)3=32,第100位数字是7.设前一个小圆点加在“4”的上面,这时循环周期是4,(100-3)4=24…1,第100位数字是4.设前一个小圆点加在“3”的上面,这时的循环周期是5,(100-2)5=19…3,第100位数字正好是5.
[注]拿到此题后容易看出后一个小圆点应加在7的上面,但前一个圆点应加在哪个数字上,一下子难以确定,怎么办?唯一的办法就是“试”.因为循环节肯定要包含5,就从数字5开始试.逐步向前移动,直到成功为止.这就像我们在迷宫中行走,不知道该走哪条道才能走出迷宫,唯一的办法就是探索:先试一试这条,再试一试那条.
9. 2
由特例不难归纳出:
(1)9的连乘积的个位数字按9,1循环出现,周期为2;
(2)8的连乘积的个位数字按8,4,2,6循环出现,周期为4;
(3)7的连乘积的个位数字按7,9,3,1循环出现,周期为4.
因为1991=9952+1,所以1991个9的连乘积的个位数字是9;因为1990=4974+2,所以1990个8的连乘积的个位数字是4;因为1989=4974+1,所以1989个7的连乘积的个位数字是7.947的个位数字是2,即1991个9与1990个8与1989年7的连乘积的个位数字是2.
10. 9
7的连乘积,尾数(个位数字)以7,9,3,1循环出现,周期为4.因为367(4=91…3,所以,367367的尾数为3.
2的连乘积,尾数以2,4,8,6循环出现,周期为4.因为762(4=190…2,所以,762762的尾数为4.
3的连乘积,尾数以3,9,7,1循环出现,周期为4.123(4
=30…3,所以,123123的尾数为7.
所以,(367367+762762)(123123的尾数为(3+4)(7=49的尾数,所求答案为9.
11. 从1开始,将每10个数分为一组,每一组10个数从右到左第一个不等于零的数字是乘积12345678910=3628800从右到左第一个不等于零的数字是8,1~1991可分为1~10,11~20,21~30,…,1981~1990,1991;8的连乘积末位数字8、4,2,6重复出现,1994=49…3,所以199个8相乘的末位数字是2,1991个位数字是1,所以,乘积123…19901991从右到左第一个不等于零的数字是2.
12. 因为第一个数=第二个数,所以第一个数:第二个数=:=3:10.又两数互质,所以第一个数为3,第二个数为10,从而这串数为:
3,10,13,23,36,59,95,154,249,403,652,1055……
被3除所得的余数为:
0,1,1,2,0,2,2,1,0,1,1,2,……按“0,1,1,2,0,2,2,1”循环,周期为8.
因为19918=248…7,所以第1991个数被3除所得余数应是第249周期中的第7个数,即2.
[注]解答此题应注意以下两个问题:
(1)由于两个数互质,所以这两个数只能是最简整数比的两个数;
(2)求出这串数被3除所得的余数后,找出余数变化的周期,但这并不是这串数的周期.一般来说,一些有规律的数串,被某一个整数逐个去除,所得的余数也具有周期性.
13. 因为“共产党好”四个字,“社会主义好”五个字,
4与5的最小公倍数是20,所以在连续写完5个“共产党好”与4个“社会主义好”之后,将重复从头写起,出现周期现象,而且每个周期是20组数.
因为34020=17,所以第340组正好写完第17个周期,第340组是(好,好).
[注]此题从题面上看是一个文字游戏,其实质是一个周期的问题:
四个四个地数
0 1 2 3 4 5 6 7 8 9 10
五个五个地数
14. 根据题意甲、乙从同一端点开始涂色,甲按黑、白,黑、白……交替进行;乙按白、黑,白、黑……交替进行,如下图所示.
由上图可知,甲黑、乙白从同一端点起,到再一次甲黑、乙白同时出现,应是5与6的最小公倍数的2倍,即562=60厘米,也就是它们按60厘米为周期循环出现.并且在每一个周期中没有涂色的部分是
1+3+5+4+2=15(厘米)
所以,在3米的木棍上没有涂黑色的部分长度总和是
15((300(60)=75(厘米)
[注]请注意这里的周期是5与6最小公倍数的2倍,而不是5与6的最小公倍数.这是同学们容易犯的错误.
年级 班 姓名 得分
一、填空题
1. 某年的二月份有五个星期日,这年六月一日是星期_____.
2. 1989年12月5日是星期二,那么再过十年的12月5日是星期_____.
3. 按下面摆法摆80个三角形,有_____个白色的.
……
4.节日的校园内挂起了一盏盏小电灯,小明看出每两个白灯之间有红、黄、绿各一盏彩灯.也就是说,从第一盏白灯起,每一盏白灯后面都紧接着有3盏彩灯,小明想第73盏灯是_____灯.
5. 时针现在表示的时间是14时正,那么分针旋转1991周后,时针表示的时间是_____.
6. 把自然数1,2,3,4,5……如表依次排列成5列,那么数“1992”在_____列.
第一列
第二列
第三列
第四列
第五列
1
2
3
4
5
9
8
7
6
10
11
12
13
14
18
17
16
15
…
…
…
…
…
…
…
…
…
7. 把分数化成小数后,小数点第110位上的数字是_____.
8. 循环小数与.这两个循环小数在小数点后第_____位,首次同时出现在该位中的数字都是7.
9. 一串数: 1,9,9,1,4,1, 4,1,9,9,1,4,1,4,1,9,9,1,4,……共有1991个数.
(1)其中共有_____个1,_____个9_____个4;
(2)这些数字的总和是_____.
10. 所得积末位数是_____.
二、解答题
11. 紧接着1989后面一串数字,写下的每个数字都是它前面两个数字的乘积的个位数.例如89=72,在9后面写2,92=18,在2后面写8,……得到一串数字:
1 9 8 9 2 8 6……
这串数字从1开始往右数,第1989个数字是什么?
12. 1991个1990相乘所得的积与1990个1991相乘所得的积,再相加的和末两位数是多少?
13. 设,那么n的末两位数字是多少?
14.在一根长100厘米的木棍上,自左至右每隔6厘米染一个红点,同时自右至左每隔5厘米也染一个红点,然后沿红点处将木棍逐段锯开,那么长度是1厘米的短木棍有多少根?
八 周期性问题(B)
年级 班 姓名 得分
一、填空题
1. 1992年1月18日是星期六,再过十年的1月18日是星期_____.
2. 黑珠、白珠共102颗,穿成一串,排列如下图:
……
这串珠子中,最后一颗珠子应该是_____色的,这种颜色的珠子在这串中共有_____颗.
3. 流水线上生产小木珠涂色的次序是:先5个红,再4个黄,再3个绿,再2个黑,再1个白,然后再依次是5红,4黄,3绿,2黑,1白,……继续下去第1993个小珠的颜色是_____色.
4. 把珠子一个一个地如下图按顺序往返不断投入A、B、C、D、E、F袋中.第1992粒珠子投在_____袋中.
5. 将数列1,4,7,10,13…依次如图排列成6行,如果把最左边的一列叫做第一列,从左到右依次编号,那么数列中的数349应排在第_____行第_____列.
1 4 7 10 13
28 25 22 19 16
31 34 37 40 43
58 55 52 49 46
………………………………
………………………………
6.分数化成小数后,小数点后面第1993位上的数字是_____.
7. 化成小数后,小数点后面1993位上的数字是_____.
8. 在一个循环小数0.1234567中,如果要使这个循环小数第100位的数字是5,那么表示循环节的两个小圆点,应分别在_____和_____这两个数字上.
9. 1991个9与1990个8与1989个7的连乘积的个位数是_____.
10. 算式(367367+762762) 123123的得数的尾数是_____.
二、解答题
11. 乘积1234……19901991是一个多位数,而且末尾有许多零,从右到左第一个不等于零的数是多少?
12.有串自然数,已知第一个数与第二个数互质,而且第一个数的恰好是第二个数的,从第三个数开始,每个数字正好是前两个数的和,问这串数的第1991个数被3除所得的余数是几?
共产党好共产党好共产党好……
社会主义好社会主义好社会主义好……
上表中,将每列上下两个字组成一组,例如第一组为(共社),第二组为(产会),那么第340组是_____.
14. 甲、乙二人对一根3米长的木棍涂色.首先,甲从木棍端点开始涂黑5厘米,间隔5厘米不涂色,接着再涂黑5厘米,这样交替做到底.然后,乙从木棍同一端点开始留出6厘米不涂色,接着涂黑6厘米,再间隔6厘米不涂色,交替做到底.最后,木棍上没有被涂黑部分的长度总和为_____厘米.
———————————————答 案——————————————————————
1. 二
因为74=28,由某年二月份有五个星期日,所以这年二月份应是29天,且2月1日与2月29日均为星期日,3月1日是星期一,所以从这年3月1日起到这年6月1日共经过了
31+30+31+1=93(天).
因为93(7=13…2,所以这年6月1日是星期二.
2. 日
依题意知,这十年中1992年、1996年都是闰年,因此,这十年之中共有
36510+2=3652(天)
因为(3652+1)7=521…6,所以再过十年的12月5日是星期日.
[注]上述两题(题1—题2)都是推断若干天、若干月或若干年后某一天为星期几,解答这类问题主要依据每周为七天循环的规律,运用周期性解答.在计算天数时,要根据“四年一闰,整百不闰,四百年才又一闰”的规定,即公历年份不是整百数时,只要是4的倍数就是闰年,公历年数为整百数时,必须是400的倍数才是闰年.
3. 39
从图中可以看出,三角形按“二黑二白一黑一白”的规律重复排列,也就是这一排列的周期为6,并且每一周期有3个白色三角形.
因为806=13…2,而第十四期中前两个三角形都是黑色的,所以共有白色三角形133=39(个).
4. 白
依题意知,电灯的安装排列如下:
白,红,黄,绿,白,红,黄,绿,白,……这一排列是按“白,红,黄,绿”交替循环出现的,也就是这一排列的周期为4.
由734=18…1,可知第73盏灯是白灯.
5. 13时.
分针旋转一周为1小时,旋转1991周为1991小时.一天24小时,199124=82…23,1991小时共82天又23小时.现在是14时正,经过82天仍然是14时正,再过23小时,正好是13时.
[注]在圆面上,沿着圆周把1到12的整数等距排成一个圈,再加上一根长针和一根短针,就组成了我们天天见到的钟面.钟面虽然是那么的简单平常,但在钟面上却包含着十分有趣的数学问题,周期现象就是其中的一个重要方面.
6. 3
仔细观察题中数表.
1 2 3 4 5 (奇数排)
第一组
8 7 6 (偶数排)
10 11 12 13 14 (奇数排)
第二组
18 17 16 15 (偶数排)
19 20 21 22 23 (奇数排)
第三组
27 26 25 24 (偶数排)
可发现规律如下:
(1)连续自然数按每组9个数,且奇数排自左往右五个数,偶数排自右往左四个数的规律循环排列;
(2)观察第二组,第三组,发现奇数排的数如果用9除有如下规律:第1列用9除余数为1,第2列用9除余数为2,…,第5列用9除余数为5.
(3)109=1…1,10在1+1组,第1列
199=2…1,19在2+1组,第1列
因为19929=221…3,所以1992应排列在(221+1)=222组中奇数排第3列数的位置上.
7. 7
=0.57142857……
它的循环周期是6,具体地六个数依次是
5,7,1,4,2,8
1106=18…2
因为余2,第110个数字是上面列出的六个数中的第2个,就是7.
8. 35
因为0.1992517的循环周期是7,0.34567的循环周期为5,又5和7的最小公倍数是35,所以两个循环小数在小数点后第35位,首次同时出现在该位上的数字都是7.
9. 853,570,568,8255.
不难看出,这串数每7个数即1,9,9,1,4,1,4为一个循环,即周期为7,且每个周期中有3个1,2个9,2个4.因为1991(7=284…3,所以这串数中有284个周期,加上第285个周期中的前三个数1,9,9.其中1的个数是:3(284+1=853(个),9的个数是2(284+2=570(个),4的个数是2(284=568(个).这些数字的总和为
1(853+9(570+4(568=8255.
10. 9
先找出积的末位数的变化规律:
71末位数为7,72末位数为9,73末位数为3, 74末位数1;75=74+1末位数为7,76=74+2末位数为9,77=74+3末位数为3,78=末位数为1……
由此可见,积的末位依次为7,9,3,1,7,9,3,1……,以4为周期循环出现.
因为504=12…2,即750=,所以750与72末位数相同,也就是积的末位数是9.
11. 依照题述规则多写几个数字:
1989286884286884……
可见1989后面的数总是不断循环重复出现286884,每6个一组,即循环周期为6.因为(1989-4)6=330…5,所以所求数字是8.
12. 1991个1990相乘所得的积末两位是0,我们只需考察1990个1991相乘的积末两位数即可.1个1991末两位数是91,2个1991相乘的积末两位数是81,3个1991相乘的积末两位数是71,4个至10个1991相乘的积的末两位数分别是61,51,41,31,21,11,01,11个1991相乘积的末两位数字是91,……,由此可见,每10个1991相乘的末两位数字重复出现,即周期为10.因为199010=199,所以1990个1991相乘积的末两位数是01,即所求结果是01.
13. n是1991个2的连乘积,可记为n=21991,首先从2的较低次幂入手寻找规律,列表如下:
n
n的十位数字
n的个位数字
n
n的十位数字
n的个位数字
21
0
2
212
9
6
22
0
4
213
9
2
23
0
8
214
8
4
24
1
6
215
6
8
25
3
2
216
3
6
26
6
4
217
7
2
27
2
8
218
4
4
28
5
6
219
8
8
29
1
2
220
7
6
210
2
4
221
5
2
211
4
8
222
0
4
观察上表,容易发现自22开始每隔20个2的连乘积,末两位数字就重复出现,周期为20.因为199020=99…10,所以21991与211的末两位数字相同,由上表知211的十位数字是4,个位数字是8.所以,n的末两位数字是48.
14. 因为100能被5整除,所以自右至左染色也就是自左至右染色.于是我们可以看作是从同一端点染色.
6与5的最小公倍数是30,即在30厘米的地方,同时染上红色,这样染色就会出现循环,每一周的长度是30厘米,如下图所示.
由图示可知长1厘米的短木棍,每一周期中有两段,如第1周期中,6-5=1,55-64=1.剩余10厘米中有一段.所以锯开后长1厘米的短木棍共有7段.综合算式为:
2[(100-10)30]+1
=23+1
=7(段)
[注]解决这一问题的关键是根据整除性把自右向左每隔5厘米的染色,转化为自左向右的染色,便于利用最小公倍数发现周期现象,化难为易.
———————————————答 案——————————————————————
1. 五
在这十年中有3个闰年,所以这10年的总天数是36510+3,365被7除余1,所以总天数被7除的余数是(13-7=)6,因此10年后的1月18日是星期五.
2. 黑,26
根据图示可知,若去掉第一颗白珠后它们的排列是按“一黑三色”交替循环出现的,也就是这一排列的周期为4.
由(102-1)4=25…1,可知循环25个周期,最后一颗珠子是黑色的.黑色珠子共有
125+1=26(颗).
3. 黑
小木球是依次按5红,4黄,3绿,2黑和1白的规律涂色的,把它看成周期性问题,每个周期为15.
由199315=132…13知,第1993个小球是第133周期中的第13个,按规律涂色应该是黑色,所以第1993个小球的颜色是黑色.
4. B
通过观察可以发现,第11次到第20次投进的袋子依次与第1次到第10次投进的袋子相同,即当投的次数被10除余1,2,3,…,8,9,0,分别投进A,B,C,……D,C,B袋中,1992被10除余2,所以第1992粒珠子投在B袋中.
5. 24,2
这个数列从第2项起,每一项都比前一项多3,(349-1)3+1=117,所以349是这列数中的第117个数.
从排列可以看出,每两排为一个周期,每一周期有10个数.
因为11710=11…7,所以数“349”是第11个周期的第7个数,也就是在第24行第2列.
6. 6
=
它的循环周期是6,因为1993=6332+1,所以化成小数后,其小数点后面第1993位上的数字是6.
7. 7
=
它的循环周期是6,因为(1993-1)6=332,则循环节“142857”恰好重复出现332次.所以小数点后面第1993位上的数字是7.
8. 3,7
表示循环小数的两个小圆点中,后一个小圆点显然应加在7的上面,且数字“5”肯定包含在循环节中,设前一个小圆点加在“5”的上面,这时循环周期是3,(100-4)3=32,第100位数字是7.设前一个小圆点加在“4”的上面,这时循环周期是4,(100-3)4=24…1,第100位数字是4.设前一个小圆点加在“3”的上面,这时的循环周期是5,(100-2)5=19…3,第100位数字正好是5.
[注]拿到此题后容易看出后一个小圆点应加在7的上面,但前一个圆点应加在哪个数字上,一下子难以确定,怎么办?唯一的办法就是“试”.因为循环节肯定要包含5,就从数字5开始试.逐步向前移动,直到成功为止.这就像我们在迷宫中行走,不知道该走哪条道才能走出迷宫,唯一的办法就是探索:先试一试这条,再试一试那条.
9. 2
由特例不难归纳出:
(1)9的连乘积的个位数字按9,1循环出现,周期为2;
(2)8的连乘积的个位数字按8,4,2,6循环出现,周期为4;
(3)7的连乘积的个位数字按7,9,3,1循环出现,周期为4.
因为1991=9952+1,所以1991个9的连乘积的个位数字是9;因为1990=4974+2,所以1990个8的连乘积的个位数字是4;因为1989=4974+1,所以1989个7的连乘积的个位数字是7.947的个位数字是2,即1991个9与1990个8与1989年7的连乘积的个位数字是2.
10. 9
7的连乘积,尾数(个位数字)以7,9,3,1循环出现,周期为4.因为367(4=91…3,所以,367367的尾数为3.
2的连乘积,尾数以2,4,8,6循环出现,周期为4.因为762(4=190…2,所以,762762的尾数为4.
3的连乘积,尾数以3,9,7,1循环出现,周期为4.123(4
=30…3,所以,123123的尾数为7.
所以,(367367+762762)(123123的尾数为(3+4)(7=49的尾数,所求答案为9.
11. 从1开始,将每10个数分为一组,每一组10个数从右到左第一个不等于零的数字是乘积12345678910=3628800从右到左第一个不等于零的数字是8,1~1991可分为1~10,11~20,21~30,…,1981~1990,1991;8的连乘积末位数字8、4,2,6重复出现,1994=49…3,所以199个8相乘的末位数字是2,1991个位数字是1,所以,乘积123…19901991从右到左第一个不等于零的数字是2.
12. 因为第一个数=第二个数,所以第一个数:第二个数=:=3:10.又两数互质,所以第一个数为3,第二个数为10,从而这串数为:
3,10,13,23,36,59,95,154,249,403,652,1055……
被3除所得的余数为:
0,1,1,2,0,2,2,1,0,1,1,2,……按“0,1,1,2,0,2,2,1”循环,周期为8.
因为19918=248…7,所以第1991个数被3除所得余数应是第249周期中的第7个数,即2.
[注]解答此题应注意以下两个问题:
(1)由于两个数互质,所以这两个数只能是最简整数比的两个数;
(2)求出这串数被3除所得的余数后,找出余数变化的周期,但这并不是这串数的周期.一般来说,一些有规律的数串,被某一个整数逐个去除,所得的余数也具有周期性.
13. 因为“共产党好”四个字,“社会主义好”五个字,
4与5的最小公倍数是20,所以在连续写完5个“共产党好”与4个“社会主义好”之后,将重复从头写起,出现周期现象,而且每个周期是20组数.
因为34020=17,所以第340组正好写完第17个周期,第340组是(好,好).
[注]此题从题面上看是一个文字游戏,其实质是一个周期的问题:
四个四个地数
0 1 2 3 4 5 6 7 8 9 10
五个五个地数
14. 根据题意甲、乙从同一端点开始涂色,甲按黑、白,黑、白……交替进行;乙按白、黑,白、黑……交替进行,如下图所示.
由上图可知,甲黑、乙白从同一端点起,到再一次甲黑、乙白同时出现,应是5与6的最小公倍数的2倍,即562=60厘米,也就是它们按60厘米为周期循环出现.并且在每一个周期中没有涂色的部分是
1+3+5+4+2=15(厘米)
所以,在3米的木棍上没有涂黑色的部分长度总和是
15((300(60)=75(厘米)
[注]请注意这里的周期是5与6最小公倍数的2倍,而不是5与6的最小公倍数.这是同学们容易犯的错误.
同课章节目录
