沪教版(五四学制)六上册:4.3 圆的面积 学案(无答案)
文档属性
| 名称 | 沪教版(五四学制)六上册:4.3 圆的面积 学案(无答案) |
|
|
| 格式 | zip | ||
| 文件大小 | 17.5KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 沪教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-04 00:00:00 | ||
图片预览

文档简介
圆的面积
【学习目标】
1.使学生理解圆面积的含义,理解圆面积计算公式的推导过程,掌握圆面积的计算公式。
2.培养学生动手操作、抽象概括的能力,运用所学知识解决简单实际问题。
3.渗透转化的数学思想。
【学习重难点】
1.圆面积的含义;圆面积的推导过程。
2.圆面积的推导过程。
【学习过程】
一、预习任务:
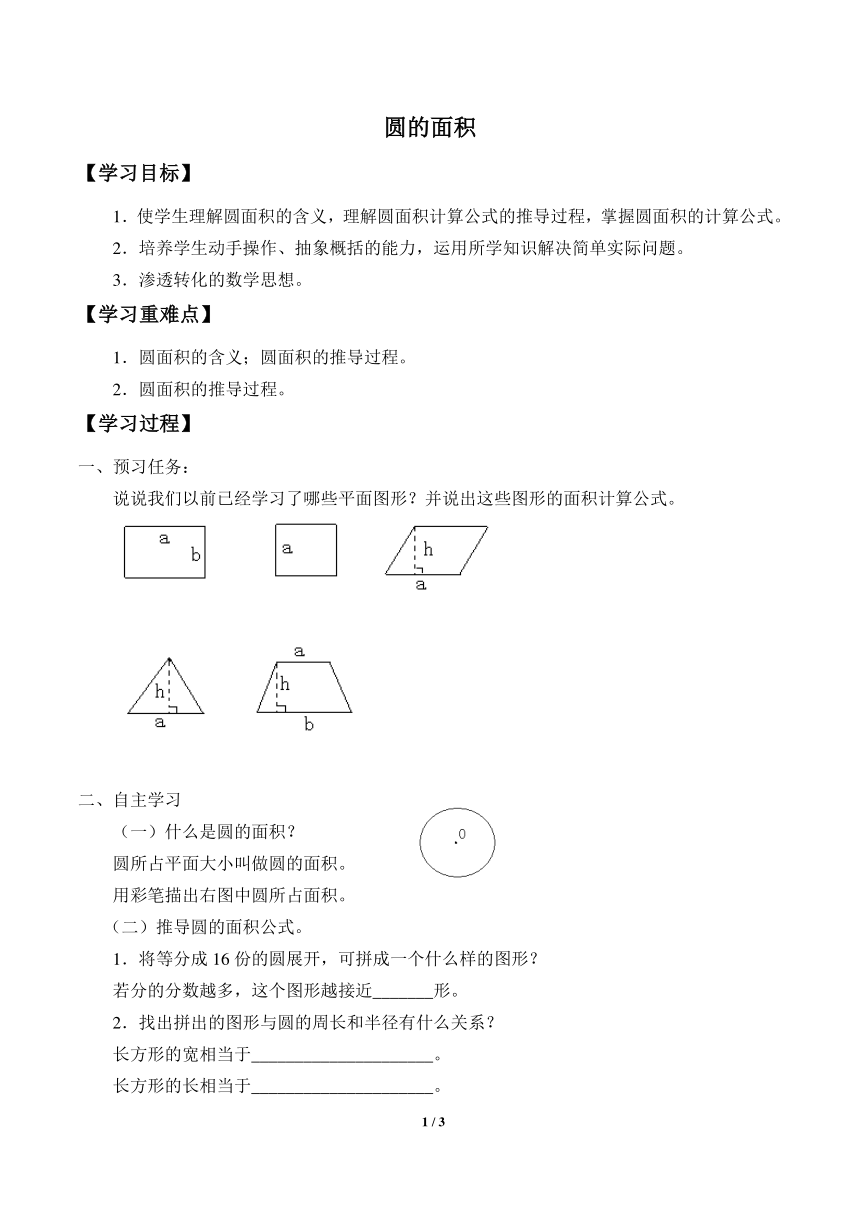
说说我们以前已经学习了哪些平面图形?并说出这些图形的面积计算公式。
二、自主学习
(一)什么是圆的面积?
圆所占平面大小叫做圆的面积。
用彩笔描出右图中圆所占面积。
(二)推导圆的面积公式。
1.将等分成16份的圆展开,可拼成一个什么样的图形?
若分的分数越多,这个图形越接近_______形。
2.找出拼出的图形与圆的周长和半径有什么关系?
长方形的宽相当于_____________________。
长方形的长相当于_____________________。
长方形面积=_____________________。
所以:圆的面积=_____________________。
公式:S =_____________________=_____________________=_____________________。
(三)圆环的面积
光盘的银色部分是一个圆环,内圆半径是2cm,外圆半径是6cm。它的面积是多少?
总结计算圆环面积的方法:
__________________________________________。
(四)应用
一个圆形花坛的直径是20m,它的面积是多少平方米?
_____________________。
三、当堂检测
(一)填空。
1.C=____________________=____________________;
S=____________________=____________________。
2.圆的半径扩大2倍,直径就扩大_________倍,周长就扩大_________倍,面积就扩大_________倍。
3.大圆半径是小圆半径的4倍,大圆周长是小圆周长的_________倍,小圆面积是大圆面积的_________。
4.圆的半径增加1/4,圆的周长增加_________,圆的面积增加_________。
5.用圆规画一个周长50.24厘米的圆,圆规两脚尖之间的距离应是_________厘米,画出的这个圆的面积是_________平方厘米。
6.大圆半径是小圆半径的2倍,大圆面积比小圆面积多12平方厘米,小圆面积是_________平方厘米。
7.一个半圆的周长是20.56分米,这个半圆的面积是_________平方分米。
8.将一个圆平均分成1000个完全相同的小扇形,割拼成近似的长方形的周长比原来圆周长长10厘米,这个长方形的面积是_________平方厘米。
(二)判断对错。
(1)通过圆心的线段,叫做圆的直径。(?? ?)
(2)周长是所在圆直径的3.14倍。(? ??)
(3)半径是直径的一半。(? ??)
(4)任何圆的圆周率都是( 。(?? ?)
(三)解决问题。
1.根据下面所给的条件,求圆的面积。
(1)r=5cm;???
???
(2)d =0.8dm;??????
(3)C=6.28m
2.公园草地上一个自动旋转喷灌装置的射程是10m。它能喷灌的面积是多少?
____________________________________________________。
3.校园圆形花池的半径是6米,在花池的周围修一条1米宽的水泥路,求水泥路的面积是多少平方米?
____________________________________________________。
4.自行车轮胎外直径71厘米,每分钟滚动100圈。通过一座1000米的大桥约需几分钟?
____________________________________________________。
【学习目标】
1.使学生理解圆面积的含义,理解圆面积计算公式的推导过程,掌握圆面积的计算公式。
2.培养学生动手操作、抽象概括的能力,运用所学知识解决简单实际问题。
3.渗透转化的数学思想。
【学习重难点】
1.圆面积的含义;圆面积的推导过程。
2.圆面积的推导过程。
【学习过程】
一、预习任务:
说说我们以前已经学习了哪些平面图形?并说出这些图形的面积计算公式。
二、自主学习
(一)什么是圆的面积?
圆所占平面大小叫做圆的面积。
用彩笔描出右图中圆所占面积。
(二)推导圆的面积公式。
1.将等分成16份的圆展开,可拼成一个什么样的图形?
若分的分数越多,这个图形越接近_______形。
2.找出拼出的图形与圆的周长和半径有什么关系?
长方形的宽相当于_____________________。
长方形的长相当于_____________________。
长方形面积=_____________________。
所以:圆的面积=_____________________。
公式:S =_____________________=_____________________=_____________________。
(三)圆环的面积
光盘的银色部分是一个圆环,内圆半径是2cm,外圆半径是6cm。它的面积是多少?
总结计算圆环面积的方法:
__________________________________________。
(四)应用
一个圆形花坛的直径是20m,它的面积是多少平方米?
_____________________。
三、当堂检测
(一)填空。
1.C=____________________=____________________;
S=____________________=____________________。
2.圆的半径扩大2倍,直径就扩大_________倍,周长就扩大_________倍,面积就扩大_________倍。
3.大圆半径是小圆半径的4倍,大圆周长是小圆周长的_________倍,小圆面积是大圆面积的_________。
4.圆的半径增加1/4,圆的周长增加_________,圆的面积增加_________。
5.用圆规画一个周长50.24厘米的圆,圆规两脚尖之间的距离应是_________厘米,画出的这个圆的面积是_________平方厘米。
6.大圆半径是小圆半径的2倍,大圆面积比小圆面积多12平方厘米,小圆面积是_________平方厘米。
7.一个半圆的周长是20.56分米,这个半圆的面积是_________平方分米。
8.将一个圆平均分成1000个完全相同的小扇形,割拼成近似的长方形的周长比原来圆周长长10厘米,这个长方形的面积是_________平方厘米。
(二)判断对错。
(1)通过圆心的线段,叫做圆的直径。(?? ?)
(2)周长是所在圆直径的3.14倍。(? ??)
(3)半径是直径的一半。(? ??)
(4)任何圆的圆周率都是( 。(?? ?)
(三)解决问题。
1.根据下面所给的条件,求圆的面积。
(1)r=5cm;???
???
(2)d =0.8dm;??????
(3)C=6.28m
2.公园草地上一个自动旋转喷灌装置的射程是10m。它能喷灌的面积是多少?
____________________________________________________。
3.校园圆形花池的半径是6米,在花池的周围修一条1米宽的水泥路,求水泥路的面积是多少平方米?
____________________________________________________。
4.自行车轮胎外直径71厘米,每分钟滚动100圈。通过一座1000米的大桥约需几分钟?
____________________________________________________。
