6.4 数据的离散程度 同步练习(解析版)
文档属性
| 名称 | 6.4 数据的离散程度 同步练习(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.1MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-03 09:17:04 | ||
图片预览


文档简介
初中数学北师大版八年级上学期 第六章 6.4 数据的离散程度
一、单选题
1.方差是刻画数据波动程度的量,对于一组数据x·x1·…xn , 可用如下算式计算方差s2= [(x1-5)2+(x2-5)2+.…+(xn-5)2],其中“5”是这组数据的(?? ) 21教育网
A.?最小值?????????????????????????????????B.?平均数?????????????????????????????????C.?中位数?????????????????????????????????D.?众数
2.已知一组数据的方差是3,则这组数据的标准差是( ??)
A.???????????????????????????????????????????B.?3??????????????????????????????????????????C.???????????????????????????????????????????D.?9
3.甲,乙,丙,丁四名同学在学校演讲选拔赛的成绩平均数 与方差s2如下表所示:
甲
乙
丙
丁
平均数
8.0
8.0
8.5
8.5
方差s2
3.5
15.5
3.5
16.5
根据表中数据,要从中选一名成绩好又发挥稳定的同学参加市演讲比赛,应该选择(??? )
A.?甲?????????????????????????????????????????B.?乙?????????????????????????????????????????C.?丙?????????????????????????????????????????D.?丁
4.为了考察甲、乙两块地小麦的长势,分别从中抽出10株苗,测出苗高,以下统计量中可以比较出两地长势哪一块更整齐的是(??? ) 21cnjy.com
?
A.?平均数??????????????????????????????????B.?中位数??????????????????????????????????C.?方差??????????????????????????????????D.?众数
5.下表记录了甲、乙、丙、丁四名运动员参加男子跳高选拔赛成绩的平均数x与方差S2:
甲
乙
丙
丁
平均数 (cm)
175
173
175
174
方差S2(cm2)
3.5
3.5
12.5
15
根据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择(?? )
A.?甲?????????????????????????????????????????B.?乙?????????????????????????????????????????C.?丙?????????????????????????????????????????D.?丁
二、填空题
6.已知一组数据5,8,10,x,9的众数是8,那么这组数据的方差是________?。
7.为了考察甲、乙两块地小麦的长势,分别从中随机抽出10株苗,测得苗高如图所示.若 和 分别表示甲、乙两块地苗高数据的方差,则 ________ .(填“>”、“<”或“=”).
8.若八个数据x1 , x2 , x3 , ……x8 , 的平均数为8,方差为1,增加一个数据8后所得的九个数据x1 , x2 , x3 , …x8;8的平均数 ?________8,方差为S2 ________1.(填“>”、“=”、“<”)
三、综合题
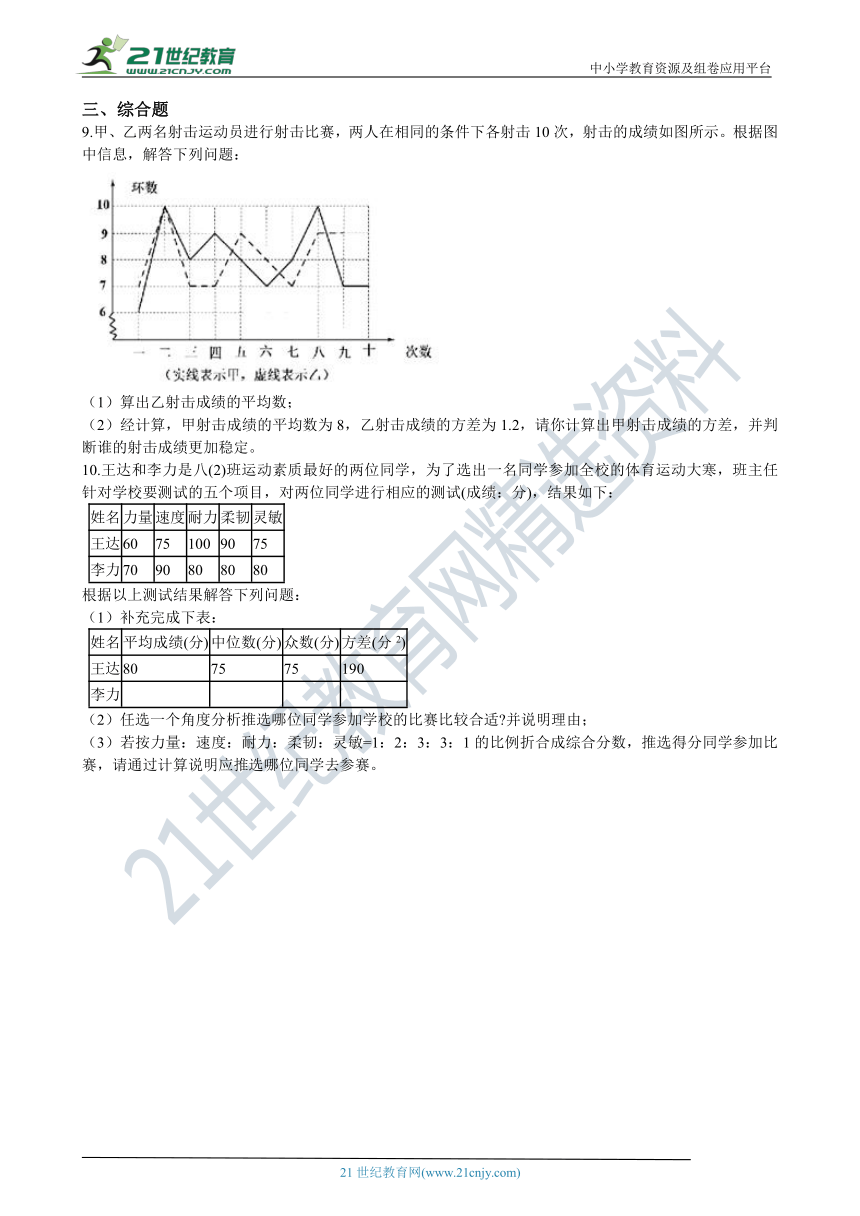
9.甲、乙两名射击运动员进行射击比赛,两人在相同的条件下各射击10次,射击的成绩如图所示。根据图中信息,解答下列问题: 21·cn·jy·com
(1)算出乙射击成绩的平均数;
(2)经计算,甲射击成绩的平均数为8,乙射击成绩的方差为1.2,请你计算出甲射击成绩的方差,并判断谁的射击成绩更加稳定。 21·世纪*教育网
10.王达和李力是八(2)班运动素质最好的两位同学,为了选出一名同学参加全校的体育运动大寒,班主任针对学校要测试的五个项目,对两位同学进行相应的测试(成绩:分),结果如下:
姓名
力量
速度
耐力
柔韧
灵敏
王达
60
75
100
90
75
李力
70
90
80
80
80
根据以上测试结果解答下列问题:
(1)补充完成下表:
姓名
平均成绩(分)
中位数(分)
众数(分)
方差(分2)
王达
80
75
75
190
李力
(2)任选一个角度分析推选哪位同学参加学校的比赛比较合适?并说明理由;
(3)若按力量:速度:耐力:柔韧:灵敏=1:2:3:3:1的比例折合成综合分数,推选得分同学参加比赛,请通过计算说明应推选哪位同学去参赛。 21世纪教育网版权所有
答案解析部分
一、单选题
1. B
解:依题可得:
5为这组数据的平均数.
故答案为:B.
【分析】方差公式:S2= [(x1- )2+(x2- )2+……+(xn- )2],其中 表示平均数,从而可得答案.
2. A
解:∵方差为3,∴标准差是, 故答案为:A.
【分析】根据标准差是方差的算术平方根解答即可。
3. C
解:丙丁平均成绩较高为8.5, 但丙的方差较小,成绩发挥稳定,应选丁. 故答案为:C. 【分析】根据要求,应选平均数较高,但方差较小的同学参加比赛。www.21-cn-jy.com
4. C
?解:方差可以比较出两地长势哪一块更整齐,方差越小,长势越整齐,方差越大,长势越不整齐。 故答案为:C 【分析】方差的定义是方差是各变量值与其均值离差平方的平均数,它是测算数值型数据离散程度的最重要的方法。据此定义分析可以判断。2·1·c·n·j·y
5. A
∵S甲2=3.5,S乙2=3.5,S丙2=12.5,S丁2=15,
∴S甲2=S乙2<S丙2<S丁2 ,
∵ 甲=175, 乙=173,
∴ 甲= 乙,
∴从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择甲;
故答案为:A. 【分析】根据平均数可知甲、丙成绩高,从方差看甲的方差小,成绩较稳定,据此判断即可.
二、填空题
6. 2.6
解:∵众数是8, 即8出现的次数最多, ∴x=8, 故答案为:2.6. 【来源:21·世纪·教育·网】
【分析】先根据众数的定理确定x的值,再由平均数公式求出这组数据的平均数,最后根据方差公式求出这组数据的方差即可.www-2-1-cnjy-com
7. <
解:由图可知,甲、乙两块地的苗高皆在12cm上下波动,但乙的波动幅度比甲大,
∴ 则??< 【分析】 方差用来计算每一个变量(观察值)与总体均数之间的差异,所以从图像看苗高的波动幅度, 可以大致估计甲、乙两块地苗高数据的方差。21*cnjy*com
8. =;<
解:∵ 八个数据x1 , x2 , x3 , ……x8 , 的平均数为8, ∴ ∴ ∵增加一个数8后,九个数据x1 , x2 , x3 , 8…x8的平均数为: ; ∵ 八个数据x1 , x2 , x3 , ……x8 , 的方差为1, ∴ ∴ ∵增加一个数8后,九个数据x1 , x2 , x3 , 8…x8的方差为: ; 故答案为:=,< 【来源:21cnj*y.co*m】
【分析】根据 八个数据x1 , x2 , x3 , ……x8 , 的平均数为8,方差为1 ,利用平均数和方差的计算方法,可求出, , 再分别求出9个数的平均数和方差,然后比较大小就可得出结果。【出处:21教育名师】
三、综合题
9. (1)解: (2)解: ,
∵ ;
∴乙的射击成绩更稳定.
故答案为:(1)8;(2)乙.
【分析】(1)根据平均数的计算公式得到答案即可。 (2)根据方差的计算公式计算得到方差,根据方差的性质计算得到答案即可。【版权所有:21教育】
10. (1)解:李力的平均成绩为:; 将5个数排序70,80,80,80,90, 最中间的数是80, ∴李力的测试成绩的中位数为80; ∵80出现了3次,是这组数据中出现次数最多的数, ∴这组数据的众数是80; 李力测试成绩的方差为: 填表如下21教育名师原创作品
姓名
平均成绩(分)
中位数(分)
众数(分)
方差(分2)
王达
80
75
75
190
李力
80
80
80
40
(2)解:根据表中数据可知,两人的平均成绩相同,从中位数和众数看,李力的成绩比王达的成绩好,从方差看,李力测试成绩的方差比王达次数成绩的方差小,可知李力的成绩比王达的成绩稳定,因此应该推选李力参加比赛。 (3)解: ∵ 按力量:速度:耐力:柔韧:灵敏=1:2:3:3:1的比例折合成综合分数, ∴王达的成绩为:60×1+75×2+100×3+90×3+75×1=855; 李力的成绩为:70×1+90×2+80×3+80×3+80×1=910; 910>855 ∴选李力去参加比赛. 21*cnjy*com
【分析】(1)利用平均数的计算方法求出李力测试成绩的平均数,再求出中位数和众数,然后利用方差公式求出李力测试成绩的方差,填表即可。
(2)可以根据表中数据,从两人的平均数,中位数,众数,方差进行分析,可得出结果。 (3)根据已知力量:速度:耐力:柔韧:灵敏=1:2:3:3:1的比例折合成综合分数,分别算出两人的综合分数,再比较大小即可得出去参加比赛的选手。2-1-c-n-j-y
一、单选题
1.方差是刻画数据波动程度的量,对于一组数据x·x1·…xn , 可用如下算式计算方差s2= [(x1-5)2+(x2-5)2+.…+(xn-5)2],其中“5”是这组数据的(?? ) 21教育网
A.?最小值?????????????????????????????????B.?平均数?????????????????????????????????C.?中位数?????????????????????????????????D.?众数
2.已知一组数据的方差是3,则这组数据的标准差是( ??)
A.???????????????????????????????????????????B.?3??????????????????????????????????????????C.???????????????????????????????????????????D.?9
3.甲,乙,丙,丁四名同学在学校演讲选拔赛的成绩平均数 与方差s2如下表所示:
甲
乙
丙
丁
平均数
8.0
8.0
8.5
8.5
方差s2
3.5
15.5
3.5
16.5
根据表中数据,要从中选一名成绩好又发挥稳定的同学参加市演讲比赛,应该选择(??? )
A.?甲?????????????????????????????????????????B.?乙?????????????????????????????????????????C.?丙?????????????????????????????????????????D.?丁
4.为了考察甲、乙两块地小麦的长势,分别从中抽出10株苗,测出苗高,以下统计量中可以比较出两地长势哪一块更整齐的是(??? ) 21cnjy.com
?
A.?平均数??????????????????????????????????B.?中位数??????????????????????????????????C.?方差??????????????????????????????????D.?众数
5.下表记录了甲、乙、丙、丁四名运动员参加男子跳高选拔赛成绩的平均数x与方差S2:
甲
乙
丙
丁
平均数 (cm)
175
173
175
174
方差S2(cm2)
3.5
3.5
12.5
15
根据表中数据,要从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择(?? )
A.?甲?????????????????????????????????????????B.?乙?????????????????????????????????????????C.?丙?????????????????????????????????????????D.?丁
二、填空题
6.已知一组数据5,8,10,x,9的众数是8,那么这组数据的方差是________?。
7.为了考察甲、乙两块地小麦的长势,分别从中随机抽出10株苗,测得苗高如图所示.若 和 分别表示甲、乙两块地苗高数据的方差,则 ________ .(填“>”、“<”或“=”).
8.若八个数据x1 , x2 , x3 , ……x8 , 的平均数为8,方差为1,增加一个数据8后所得的九个数据x1 , x2 , x3 , …x8;8的平均数 ?________8,方差为S2 ________1.(填“>”、“=”、“<”)
三、综合题
9.甲、乙两名射击运动员进行射击比赛,两人在相同的条件下各射击10次,射击的成绩如图所示。根据图中信息,解答下列问题: 21·cn·jy·com
(1)算出乙射击成绩的平均数;
(2)经计算,甲射击成绩的平均数为8,乙射击成绩的方差为1.2,请你计算出甲射击成绩的方差,并判断谁的射击成绩更加稳定。 21·世纪*教育网
10.王达和李力是八(2)班运动素质最好的两位同学,为了选出一名同学参加全校的体育运动大寒,班主任针对学校要测试的五个项目,对两位同学进行相应的测试(成绩:分),结果如下:
姓名
力量
速度
耐力
柔韧
灵敏
王达
60
75
100
90
75
李力
70
90
80
80
80
根据以上测试结果解答下列问题:
(1)补充完成下表:
姓名
平均成绩(分)
中位数(分)
众数(分)
方差(分2)
王达
80
75
75
190
李力
(2)任选一个角度分析推选哪位同学参加学校的比赛比较合适?并说明理由;
(3)若按力量:速度:耐力:柔韧:灵敏=1:2:3:3:1的比例折合成综合分数,推选得分同学参加比赛,请通过计算说明应推选哪位同学去参赛。 21世纪教育网版权所有
答案解析部分
一、单选题
1. B
解:依题可得:
5为这组数据的平均数.
故答案为:B.
【分析】方差公式:S2= [(x1- )2+(x2- )2+……+(xn- )2],其中 表示平均数,从而可得答案.
2. A
解:∵方差为3,∴标准差是, 故答案为:A.
【分析】根据标准差是方差的算术平方根解答即可。
3. C
解:丙丁平均成绩较高为8.5, 但丙的方差较小,成绩发挥稳定,应选丁. 故答案为:C. 【分析】根据要求,应选平均数较高,但方差较小的同学参加比赛。www.21-cn-jy.com
4. C
?解:方差可以比较出两地长势哪一块更整齐,方差越小,长势越整齐,方差越大,长势越不整齐。 故答案为:C 【分析】方差的定义是方差是各变量值与其均值离差平方的平均数,它是测算数值型数据离散程度的最重要的方法。据此定义分析可以判断。2·1·c·n·j·y
5. A
∵S甲2=3.5,S乙2=3.5,S丙2=12.5,S丁2=15,
∴S甲2=S乙2<S丙2<S丁2 ,
∵ 甲=175, 乙=173,
∴ 甲= 乙,
∴从中选择一名成绩好又发挥稳定的运动员参加比赛,应该选择甲;
故答案为:A. 【分析】根据平均数可知甲、丙成绩高,从方差看甲的方差小,成绩较稳定,据此判断即可.
二、填空题
6. 2.6
解:∵众数是8, 即8出现的次数最多, ∴x=8, 故答案为:2.6. 【来源:21·世纪·教育·网】
【分析】先根据众数的定理确定x的值,再由平均数公式求出这组数据的平均数,最后根据方差公式求出这组数据的方差即可.www-2-1-cnjy-com
7. <
解:由图可知,甲、乙两块地的苗高皆在12cm上下波动,但乙的波动幅度比甲大,
∴ 则??< 【分析】 方差用来计算每一个变量(观察值)与总体均数之间的差异,所以从图像看苗高的波动幅度, 可以大致估计甲、乙两块地苗高数据的方差。21*cnjy*com
8. =;<
解:∵ 八个数据x1 , x2 , x3 , ……x8 , 的平均数为8, ∴ ∴ ∵增加一个数8后,九个数据x1 , x2 , x3 , 8…x8的平均数为: ; ∵ 八个数据x1 , x2 , x3 , ……x8 , 的方差为1, ∴ ∴ ∵增加一个数8后,九个数据x1 , x2 , x3 , 8…x8的方差为: ; 故答案为:=,< 【来源:21cnj*y.co*m】
【分析】根据 八个数据x1 , x2 , x3 , ……x8 , 的平均数为8,方差为1 ,利用平均数和方差的计算方法,可求出, , 再分别求出9个数的平均数和方差,然后比较大小就可得出结果。【出处:21教育名师】
三、综合题
9. (1)解: (2)解: ,
∵ ;
∴乙的射击成绩更稳定.
故答案为:(1)8;(2)乙.
【分析】(1)根据平均数的计算公式得到答案即可。 (2)根据方差的计算公式计算得到方差,根据方差的性质计算得到答案即可。【版权所有:21教育】
10. (1)解:李力的平均成绩为:; 将5个数排序70,80,80,80,90, 最中间的数是80, ∴李力的测试成绩的中位数为80; ∵80出现了3次,是这组数据中出现次数最多的数, ∴这组数据的众数是80; 李力测试成绩的方差为: 填表如下21教育名师原创作品
姓名
平均成绩(分)
中位数(分)
众数(分)
方差(分2)
王达
80
75
75
190
李力
80
80
80
40
(2)解:根据表中数据可知,两人的平均成绩相同,从中位数和众数看,李力的成绩比王达的成绩好,从方差看,李力测试成绩的方差比王达次数成绩的方差小,可知李力的成绩比王达的成绩稳定,因此应该推选李力参加比赛。 (3)解: ∵ 按力量:速度:耐力:柔韧:灵敏=1:2:3:3:1的比例折合成综合分数, ∴王达的成绩为:60×1+75×2+100×3+90×3+75×1=855; 李力的成绩为:70×1+90×2+80×3+80×3+80×1=910; 910>855 ∴选李力去参加比赛. 21*cnjy*com
【分析】(1)利用平均数的计算方法求出李力测试成绩的平均数,再求出中位数和众数,然后利用方差公式求出李力测试成绩的方差,填表即可。
(2)可以根据表中数据,从两人的平均数,中位数,众数,方差进行分析,可得出结果。 (3)根据已知力量:速度:耐力:柔韧:灵敏=1:2:3:3:1的比例折合成综合分数,分别算出两人的综合分数,再比较大小即可得出去参加比赛的选手。2-1-c-n-j-y
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
