7.5 三角形内角和定理 同步练习(解析版)
文档属性
| 名称 | 7.5 三角形内角和定理 同步练习(解析版) |  | |
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 北师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-03 09:24:41 | ||
图片预览


文档简介
初中数学北师大版八年级上学期 第七章 7.5 三角形内角和定理
一、单选题
1.在 ABC中, A: B: C=2:3:5,则 ABC是(???? )
A.?锐角三角形????????????????????????B.?钝角三角形????????????????????????C.?直角三角形????????????????????????D.?不能确定
2.如图,是一块三角形木板的残余部分,量得∠A=100°,∠B=40°,这块三角形木板另外一个角∠C的度数为(?? ) 21教育网
A.?30°???????????????????????????????????????B.?40°???????????????????????????????????????C.?50°???????????????????????????????????????D.?60°
3.如图,一把直尺的边缘AB 经过一块三角板 DCB 的直角顶点B,交斜边CD 于点A,直尺的边缘EF 分别交CD、BD 于点E、F,若∠D=60°,∠ABC=20°,则∠1 的度数为(? ) 21cnjy.com
A.?25°???????????????????????????????????????B.?40°???????????????????????????????????????C.?50°???????????????????????????????????????D.?80°
4.如图,墙上钉着三根木条,a,b,c,量得∠1=70°,∠2=100°,那么木条a,b所在直线所夹的锐角是( ??)
A.?5°???????????????????????????????????????B.?10°???????????????????????????????????????C.?30°???????????????????????????????????????D.?70°
二、填空题
5.如图,求∠A+∠B+∠C+∠D+∠E的度数:________.
6.已知△ABC中,∠A∶∠B∶∠C=2∶3∶5,则△ABC是________三角形.
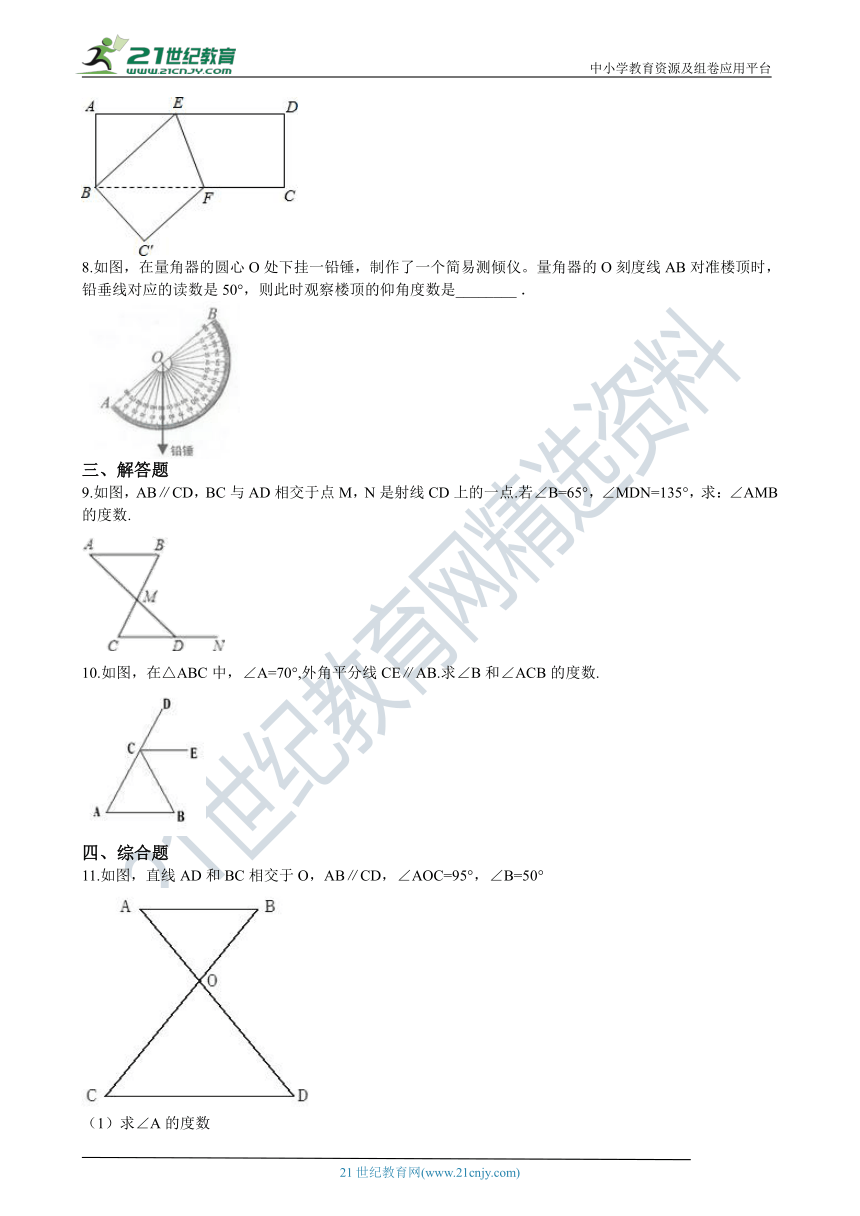
7.如图,将一张矩形纸片ABCD沿EF折叠,使点D与点B重合,点C落在C'的位置上,若∠BFE=67°,则∠ABE的度数为________. 21·世纪*教育网
8.如图,在量角器的圆心O处下挂一铅锤,制作了一个简易测倾仪。量角器的O刻度线AB对准楼顶时,铅垂线对应的读数是50°,则此时观察楼顶的仰角度数是________?. 2-1-c-n-j-y
三、解答题
9.如图,AB∥CD,BC与AD相交于点M,N是射线CD上的一点.若∠B=65°,∠MDN=135°,求:∠AMB的度数. 【来源:21cnj*y.co*m】
10.如图,在△ABC中,∠A=70°,外角平分线CE∥AB.求∠B和∠ACB的度数.
四、综合题
11.如图,直线AD和BC相交于O,AB∥CD,∠AOC=95°,∠B=50°
(1)求∠A的度数
(2)求∠D的度数
12.下列语句中,正确的是(?? )
A.?三角形的外角大于任何一个内角?????????????????????????B.?三角形的外角等于这个三角形的两个内角之和 C.?三角形的外角中,至少有两个钝角??????????????????????D.?三角形的外角中,至少有一个钝角
答案解析部分
一、单选题
1. C
解:由题意得:三角形的最大角为:180°×=90°, 故答案为:C. 【分析】根据三角形内角和定理,结合比例的关系,求出最大角,即可确定三角形的形状。
2. B
解:∵△ABC中,∠A=100°,∠B=40°,
∴∠C=180°-∠A-∠B=180°-100°-40°=40°.
故答案为:B.
【分析】根据三角形的内角和,由∠C=180°-∠A-∠B即可算出答案。
3. C
解:∵∠CBD=90°,
∴∠ABD=90°﹣∠ABC==90°-20°=70°,
∵EF∥AB,
∴∠DFE=∠ABD=70°,
∴∠DEF=180°﹣∠D﹣∠DFE=50°,
∴∠1=∠DEF=50°,
故答案为:C.
【分析】根据角的和差算出∠ABD的度数,根据二直线平行,同位角相等得出∠DFE=∠ABD=70°,根据三角形的内角和算出∠DEF的度数,最后根据对顶角相等算出∠1的度数。【来源:21·世纪·教育·网】
4. B
解:如图,
∵∠2=∠3=100°,∠1=70°
∴a、b两直线所夹的锐角为:180°-∠1-∠3=180°-70°-100°=10°
故答案为:B
【分析】根据对顶角相等,可求出∠3的度数,再利用三角形内角和定理就可求出a、b两直线所夹的锐角的度数。www-2-1-cnjy-com
二、填空题
5. 180°
解:连接AC,如图所示:
∵∠E+∠D+∠EFD=∠1+∠2+∠AFC=180°,
又∵∠EFD=∠AFC,
∴∠E+∠D=∠1+∠2,
∴∠A+∠B+∠C+∠D+∠E
=∠FAB+∠B+∠FCB+∠1+∠2
=∠BAC+∠B+∠ACB
=180゜.
故答案是:180°.
【分析】连接AC,如图所示:根据三角形的内角和定理、对顶角相等及等式的性质得出∠E+∠D=∠1+∠2,从而根据角的和差及等量代换、三角形的内角和定理即可算出答案.21*cnjy*com
6. 直角
解:设三角形三个角的度数分别为2x,3x,5x ∴2x+3x+5x=180° ∴10x=180° x=18° ∴∠A=36°,∠B=54°,∠C=90° ∴△ABC为直角三角形。 【分析】根据三角形三边的度数的比,根据三角形的内角度数和求出答案即可。【出处:21教育名师】
7. 44°
∵AD∥BC,
∴∠DEF=∠BFE=67°;
又∵∠BEF=∠DEF=67°,
∴∠AEB=180°﹣∠BEF﹣∠DEF=180°﹣67°﹣67°=46°,
∵∠A=90°,
∴∠ABE=90°﹣46°=44°,
故答案为44°.
【分析】根据直线平行的性质,即可得到∠DEF的数值,根据三角形的内角和定理求出答案即可。
8. 40°
如图,
依题可得:∠AOC=50°,
∴∠OAC=40°,
即观察楼顶的仰角度数为40°.
故答案为:40°.
【分析】根据题意可得∠AOC=50°,由三角形内角和定理得∠OAC=40°,∠OAC即为观察楼顶的仰角度数.
三、解答题
9. 解:∵AB∥CD,
∴∠A+∠MDN=180°,
∴∠A=180°﹣∠MDN=45°,
在△ABM中,∠AMB=180°﹣∠A﹣∠B=70°
【分析】根据二直线平行同旁内角互补得出 ∠A=180°﹣∠MDN=45°, 从而根据三角形的内角和定理,由 ∠AMB=180°﹣∠A﹣∠B 即可算出答案.21世纪教育网版权所有
10. 解:∵ CE∥AB , ∴∠DCE=∠CAB=70°, ∴∠DCB=140°, ∴∠ACB=180°-∠DCB=180°-140°=40°, ∴∠B=180°-∠A-∠ACB=180°-40°-70°=70°. www.21-cn-jy.com
【分析】由CE∥AB,利用平行线的性质求得∠DCE的度数,再由CE平分∠DCB,求得∠DCB的度数,利用邻补角的性质即可求出∠ACB的度数,最后利用三角形的内角和定理即可求出∠B的度数。
四、综合题
11. (1)∵∠AOC=95° ∴∠AOB=180°-95°=85° ∴∠A=180°-∠AOB-∠B=180°-85°-50°=45° (2)∵AB∥CD ∴∠A=∠D=45° 21·cn·jy·com
【分析】(1)根据平角的性质计算得到∠AOB的度数,在三角形AOB中,根据三角形的内角和定理即可得到∠A的度数。 (2)根据两直线平行,内错角相等即可计算得到∠D的度数。2·1·c·n·j·y
12. C
解:A、三角形的外角大于任何一个不相邻的内角,不符合题意; B、三角形的一个外角等于这个三角形的不相邻两个内角之和,不符合题意; CD、?因为三角形的内角至少有两个是锐角,则三个外角中,至少有两个钝角,C符合题意,D不符合题意; 故答案为:C. 【分析】三角形的一个外角等于这个三角形的不相邻两个内角之和,则三角形的外角大于任何一个不相邻的内角;?因为三角形的内角至少有两个是锐角,则三个外角中,至少有两个钝角;据此分析判断即知答案。【版权所有:21教育】
一、单选题
1.在 ABC中, A: B: C=2:3:5,则 ABC是(???? )
A.?锐角三角形????????????????????????B.?钝角三角形????????????????????????C.?直角三角形????????????????????????D.?不能确定
2.如图,是一块三角形木板的残余部分,量得∠A=100°,∠B=40°,这块三角形木板另外一个角∠C的度数为(?? ) 21教育网
A.?30°???????????????????????????????????????B.?40°???????????????????????????????????????C.?50°???????????????????????????????????????D.?60°
3.如图,一把直尺的边缘AB 经过一块三角板 DCB 的直角顶点B,交斜边CD 于点A,直尺的边缘EF 分别交CD、BD 于点E、F,若∠D=60°,∠ABC=20°,则∠1 的度数为(? ) 21cnjy.com
A.?25°???????????????????????????????????????B.?40°???????????????????????????????????????C.?50°???????????????????????????????????????D.?80°
4.如图,墙上钉着三根木条,a,b,c,量得∠1=70°,∠2=100°,那么木条a,b所在直线所夹的锐角是( ??)
A.?5°???????????????????????????????????????B.?10°???????????????????????????????????????C.?30°???????????????????????????????????????D.?70°
二、填空题
5.如图,求∠A+∠B+∠C+∠D+∠E的度数:________.
6.已知△ABC中,∠A∶∠B∶∠C=2∶3∶5,则△ABC是________三角形.
7.如图,将一张矩形纸片ABCD沿EF折叠,使点D与点B重合,点C落在C'的位置上,若∠BFE=67°,则∠ABE的度数为________. 21·世纪*教育网
8.如图,在量角器的圆心O处下挂一铅锤,制作了一个简易测倾仪。量角器的O刻度线AB对准楼顶时,铅垂线对应的读数是50°,则此时观察楼顶的仰角度数是________?. 2-1-c-n-j-y
三、解答题
9.如图,AB∥CD,BC与AD相交于点M,N是射线CD上的一点.若∠B=65°,∠MDN=135°,求:∠AMB的度数. 【来源:21cnj*y.co*m】
10.如图,在△ABC中,∠A=70°,外角平分线CE∥AB.求∠B和∠ACB的度数.
四、综合题
11.如图,直线AD和BC相交于O,AB∥CD,∠AOC=95°,∠B=50°
(1)求∠A的度数
(2)求∠D的度数
12.下列语句中,正确的是(?? )
A.?三角形的外角大于任何一个内角?????????????????????????B.?三角形的外角等于这个三角形的两个内角之和 C.?三角形的外角中,至少有两个钝角??????????????????????D.?三角形的外角中,至少有一个钝角
答案解析部分
一、单选题
1. C
解:由题意得:三角形的最大角为:180°×=90°, 故答案为:C. 【分析】根据三角形内角和定理,结合比例的关系,求出最大角,即可确定三角形的形状。
2. B
解:∵△ABC中,∠A=100°,∠B=40°,
∴∠C=180°-∠A-∠B=180°-100°-40°=40°.
故答案为:B.
【分析】根据三角形的内角和,由∠C=180°-∠A-∠B即可算出答案。
3. C
解:∵∠CBD=90°,
∴∠ABD=90°﹣∠ABC==90°-20°=70°,
∵EF∥AB,
∴∠DFE=∠ABD=70°,
∴∠DEF=180°﹣∠D﹣∠DFE=50°,
∴∠1=∠DEF=50°,
故答案为:C.
【分析】根据角的和差算出∠ABD的度数,根据二直线平行,同位角相等得出∠DFE=∠ABD=70°,根据三角形的内角和算出∠DEF的度数,最后根据对顶角相等算出∠1的度数。【来源:21·世纪·教育·网】
4. B
解:如图,
∵∠2=∠3=100°,∠1=70°
∴a、b两直线所夹的锐角为:180°-∠1-∠3=180°-70°-100°=10°
故答案为:B
【分析】根据对顶角相等,可求出∠3的度数,再利用三角形内角和定理就可求出a、b两直线所夹的锐角的度数。www-2-1-cnjy-com
二、填空题
5. 180°
解:连接AC,如图所示:
∵∠E+∠D+∠EFD=∠1+∠2+∠AFC=180°,
又∵∠EFD=∠AFC,
∴∠E+∠D=∠1+∠2,
∴∠A+∠B+∠C+∠D+∠E
=∠FAB+∠B+∠FCB+∠1+∠2
=∠BAC+∠B+∠ACB
=180゜.
故答案是:180°.
【分析】连接AC,如图所示:根据三角形的内角和定理、对顶角相等及等式的性质得出∠E+∠D=∠1+∠2,从而根据角的和差及等量代换、三角形的内角和定理即可算出答案.21*cnjy*com
6. 直角
解:设三角形三个角的度数分别为2x,3x,5x ∴2x+3x+5x=180° ∴10x=180° x=18° ∴∠A=36°,∠B=54°,∠C=90° ∴△ABC为直角三角形。 【分析】根据三角形三边的度数的比,根据三角形的内角度数和求出答案即可。【出处:21教育名师】
7. 44°
∵AD∥BC,
∴∠DEF=∠BFE=67°;
又∵∠BEF=∠DEF=67°,
∴∠AEB=180°﹣∠BEF﹣∠DEF=180°﹣67°﹣67°=46°,
∵∠A=90°,
∴∠ABE=90°﹣46°=44°,
故答案为44°.
【分析】根据直线平行的性质,即可得到∠DEF的数值,根据三角形的内角和定理求出答案即可。
8. 40°
如图,
依题可得:∠AOC=50°,
∴∠OAC=40°,
即观察楼顶的仰角度数为40°.
故答案为:40°.
【分析】根据题意可得∠AOC=50°,由三角形内角和定理得∠OAC=40°,∠OAC即为观察楼顶的仰角度数.
三、解答题
9. 解:∵AB∥CD,
∴∠A+∠MDN=180°,
∴∠A=180°﹣∠MDN=45°,
在△ABM中,∠AMB=180°﹣∠A﹣∠B=70°
【分析】根据二直线平行同旁内角互补得出 ∠A=180°﹣∠MDN=45°, 从而根据三角形的内角和定理,由 ∠AMB=180°﹣∠A﹣∠B 即可算出答案.21世纪教育网版权所有
10. 解:∵ CE∥AB , ∴∠DCE=∠CAB=70°, ∴∠DCB=140°, ∴∠ACB=180°-∠DCB=180°-140°=40°, ∴∠B=180°-∠A-∠ACB=180°-40°-70°=70°. www.21-cn-jy.com
【分析】由CE∥AB,利用平行线的性质求得∠DCE的度数,再由CE平分∠DCB,求得∠DCB的度数,利用邻补角的性质即可求出∠ACB的度数,最后利用三角形的内角和定理即可求出∠B的度数。
四、综合题
11. (1)∵∠AOC=95° ∴∠AOB=180°-95°=85° ∴∠A=180°-∠AOB-∠B=180°-85°-50°=45° (2)∵AB∥CD ∴∠A=∠D=45° 21·cn·jy·com
【分析】(1)根据平角的性质计算得到∠AOB的度数,在三角形AOB中,根据三角形的内角和定理即可得到∠A的度数。 (2)根据两直线平行,内错角相等即可计算得到∠D的度数。2·1·c·n·j·y
12. C
解:A、三角形的外角大于任何一个不相邻的内角,不符合题意; B、三角形的一个外角等于这个三角形的不相邻两个内角之和,不符合题意; CD、?因为三角形的内角至少有两个是锐角,则三个外角中,至少有两个钝角,C符合题意,D不符合题意; 故答案为:C. 【分析】三角形的一个外角等于这个三角形的不相邻两个内角之和,则三角形的外角大于任何一个不相邻的内角;?因为三角形的内角至少有两个是锐角,则三个外角中,至少有两个钝角;据此分析判断即知答案。【版权所有:21教育】
同课章节目录
- 第一章 勾股定理
- 1 探索勾股定理
- 2 一定是直角三角形吗
- 3 勾股定理的应用
- 第二章 实数
- 1 认识无理数
- 2 平方根
- 3 立方根
- 4 估算
- 5 用计算器开方
- 6 实数
- 7 二次根式
- 第三章 位置与坐标
- 1 确定位置
- 2 平面直角坐标系
- 3 轴对称与坐标变化
- 第四章 一次函数
- 1 函数
- 2 一次函数与正比例函数
- 3 一次函数的图象
- 4 一次函数的应用
- 第五章 二元一次方程组
- 1 认识二元一次方程组
- 2 求解二元一次方程组
- 3 应用二元一次方程组——鸡免同笼
- 4 应用二元一次方程组——增收节支
- 5 应用二元一次方程组——里程碑上的数
- 6 二元一次方程与一次函数
- 7 用二元一次方程组确定一次函数表达式
- 8*三元一次方程组
- 第六章 数据的分析
- 1 平均数
- 2 中位数与众数
- 3 从统计图分析数据的集中趋势
- 4 数据的离散程度
- 第七章 平行线的证明
- 1 为什么要证明
- 2 定义与命题
- 3 平行线的判定
- 4 平行线的性质
- 5 三角形的内角和定理
