5.2.2 平行线的判定 同步练习(解析版)
文档属性
| 名称 | 5.2.2 平行线的判定 同步练习(解析版) |

|
|
| 格式 | zip | ||
| 文件大小 | 1.2MB | ||
| 资源类型 | 试卷 | ||
| 版本资源 | 华东师大版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-03 09:32:52 | ||
图片预览


文档简介
初中数学华师大版七年级上学期 第5章 5.2.2 平行线的判定
一、单选题
1.如图所示,在下列四组条件中,能判定AB∥CD的是( ??)
A.?∠1=∠2???????????????????B.?∠ABD=∠BDC???????????????????C.?∠3=∠4???????????????????D.?∠BAD+∠ABC=180°
2.如图所示,下列条件中,不能判断AD∥BC的是(?? )
A.?∠1=∠4??????????????????????B.?∠3=∠4??????????????????????C.?∠2+∠3=180°??????????????????????D.?∠1+∠D=180°
3.如图,不能作为判断AE∥CD的条件的是(??? )
A.?∠FEB=∠ECD??????????????B.?∠AEC=∠ECD??????????????C.?∠BEC+∠ECD=180°??????????????D.?∠AEG=∠DCH??
4.如图,下列能判定AB∥EF的条件有(?? )
①∠B+∠BFE=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5.
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
5.如图,能判断 的条件是(?? )
A.?????????????????????B.?????????????????????C.?????????????????????D.?以上都对
6.下列命题属于真命题的是(??? )
A.?同旁内角相等,两直线平行????????????????????????????????B.?相等的角是对顶角 C.?平行于同一条直线的两条直线平行??????????????????????D.?同位角相等21·cn·jy·com
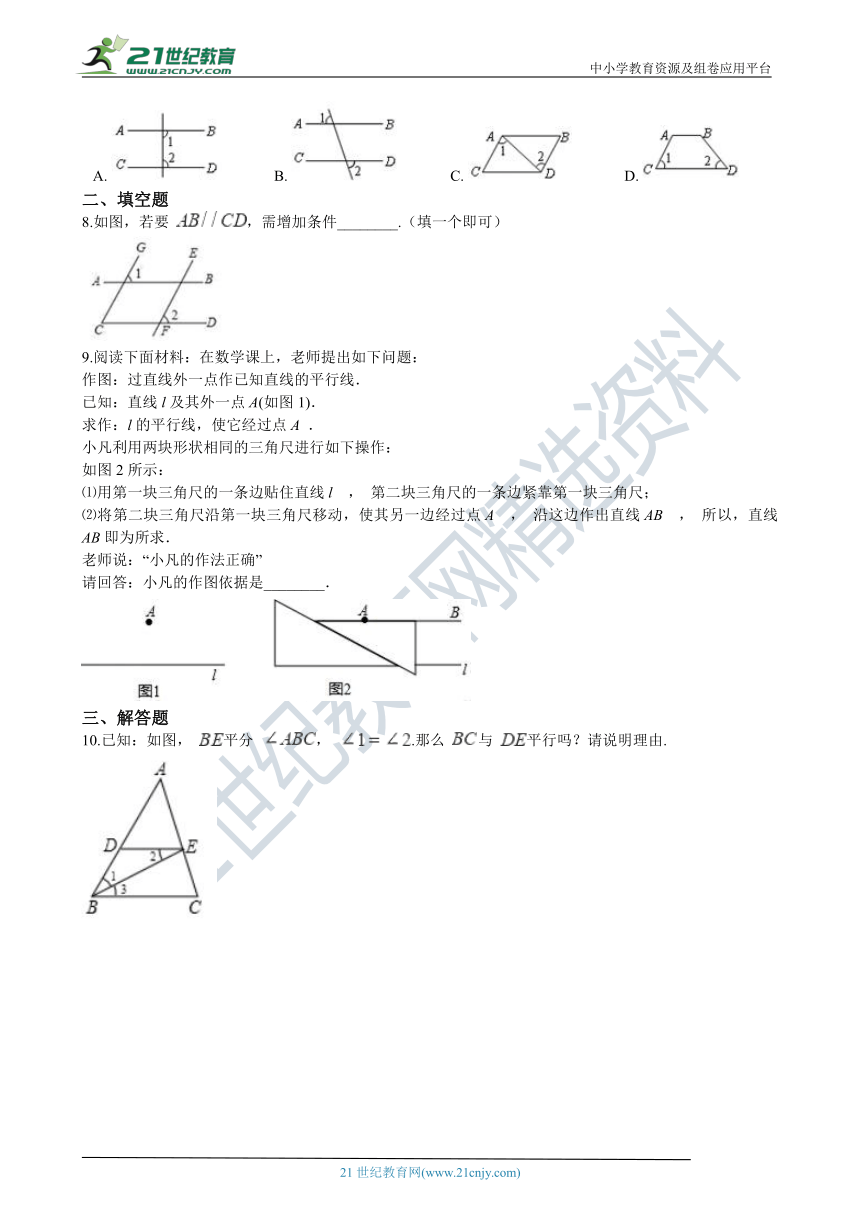
7.下列图形中,由 ,能得到 的是(??? )
A.???????????????B.???????????????C.???????????????D.?
二、填空题
8.如图,若要 ,需增加条件________.(填一个即可)
9.阅读下面材料:在数学课上,老师提出如下问题:
作图:过直线外一点作已知直线的平行线.
已知:直线l及其外一点A(如图1).
求作:l的平行线,使它经过点A .
小凡利用两块形状相同的三角尺进行如下操作:
如图2所示:
⑴用第一块三角尺的一条边贴住直线l , 第二块三角尺的一条边紧靠第一块三角尺;
⑵将第二块三角尺沿第一块三角尺移动,使其另一边经过点A , 沿这边作出直线AB , 所以,直线AB即为所求.www.21-cn-jy.com
老师说:“小凡的作法正确”
请回答:小凡的作图依据是________.
三、解答题
10.已知:如图, 平分 , .那么 与 平行吗?请说明理由.
答案解析部分
一、单选题
1. B
解:A、∵∠1=∠2,∴ AD∥BC,不符合题意; B、??∵∠ABD=∠BDC?,∴AB∥CD,符合题意; C、∵ ∠3=∠4 ,∴ AD∥BC,不符合题意; D、∵ ∠BAD+∠ABC=180°?,∴AD∥BC,不符合题意; 故答案为:B. 【分析】根据平行线的性质,即同位角相等两直线平行,内错角相等两直线平行,同旁内角互补两直线平行,逐项分析判断即可.2·1·c·n·j·y
2. A
解:A、∵∠1=∠4,∴AB∥CD(内错角相等,两直线平行),但不能判定AD∥BC;
B、∵∠3=∠4,∴AD∥BC(同位角相等,两直线平行);
C、∵∠2+∠3=180°,∴AD∥BC(同旁内角互补,两直线平行);
D、∵∠1+∠D=180°,∴AD∥BC(同旁内角互补,两直线平行);
故答案为:A.
【分析】A、∠1与∠4是直线DC,AB被BC所截的一对内错角,根据内错角相等,二直线平行得出AB∥CD,但不能判定AD∥BC,A符合题意; B、∠3与∠4是直线DA,CB被BA所截的一对同位角,根据同位角相等,二直线平行得出AD∥CB,B不符合题意; C、∠3与∠2是直线DA,CB被BA所截的一对同旁内角,根据同旁内角互补,二直线平行得出AD∥CB,B不符合题意; D、∠1与∠D是直线DA,CB被DC所截的一对同旁内角,根据同旁内角互补,二直线平行得出AD∥CB,B不符合题意,综上所述就可得出答案.21教育网
3. D
解:A、 ∠FEB=∠ECD ,则AE∥CD(同位角相等两直线平行),正确,不符合题意; B、 ∠AEC=∠ECD ,则AE∥CD(内错角相等两直线平行),正确,不符合题意; C、 ∠BEC+∠ECD=180° ,则AE∥CD(同旁内角互补两直线平行),正确,不符合题意; D、 ∠AEG和∠DCH不属于三线八角当中的一组角,不能用来判断是否平行,错误,符合题意; 故答案为:D. 【分析】利用平行线的判定定理,即同位角相等两直线平行,内错角相等两直线平行,同旁内角互补两直线平行,逐一判断即可。【来源:21·世纪·教育·网】
4. C
解:当∠B+∠BFE=180°,AB∥EF;当∠1=∠2时,DE∥BC;当∠3=∠4时,AB∥EF;当∠B=∠5时,AB∥EF. 21·纪*教育网
故答案为:C.
【分析】根据同旁内角互补两直线平行可得AB∥EF;根据内错角相等两直线平行可得DE∥BC,AB∥EF;根据同位角相等两直线平行可得AB∥EF.据此判断即可.www-2-1-cnjy-com
5. B
解:A. 与 既不是同位角又不是内错角,因而A选项无法判断 ;
B选项:如图:
由因为∠1+∠6=180°,∠6=∠2;所以当∠1+∠2=180°时,所以AB//CD,故B符合.
C. 与 既不是同位角又不是内错角,因而C选项无法判断 ;
D选项也不对.
故答案为:B.
【分析】平行线的判定方法:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补两直线平行;如图“三线八角”中,利用同角的补角相等可得∠6=∠2,利用同位角相等,两直线平行可得AB∥CD,据此判断即可.2-1-c-n-j-y
6. C
解:A、同旁内角互补,两直线平行,是假命题;
B、相等的角不一定是对顶角,是假命题;
C、平行于同一条直线的两条直线平行,是真命题;
D、两直线平行,同位角相等,是假命题。
故答案为:C。
【分析】根据平行线的判定方法,同旁内角互补,二直线平行;根据对顶角的性质,对顶角相等,但相等的角不一定是对顶角;根据平行线的传递性,平行于同一条直线的两条直线平行;根据平行线的性质,两直线平行,同位角相等,从而即可一一判断得出答案。21*cnjy*com
7. B
解:A.∵∠1=∠2是同旁内角,∴不能判断 ,故不符合题意;
B.作∠3如下图,
∵∠1=∠3,∠1=∠2,∴∠2=∠3,∴
故∠1=∠2,则 ,故符合题意;
C. ∠1=∠2可得 不能得到 ,故不符合题意;
D. ∠1=∠2不能得到 ,故不符合题意. 故答案为:B. 【分析】A、∠1=∠2是同旁内角,即使相等,也判断不出 ,故A不符合题意;
B、首先根据对顶角相等判断出∠1=∠3,再根据等量代换得出∠2=∠3,然后根据同位角相等,二直线平行得出, 故B正确,符合题意; C、根据内错角相等,二直线平行,由 ∠1=∠2可得 , 不能得到 ,故C错误,不符合题意; D、∠1=∠2是同旁内角,即使相等,也判断不出 ,故D错误,不符合题意。 ?21世纪教育网版权所有
二、填空题
8.
解: ,
(同位角相等,两直线平行),
故答案为: .
【分析】根据同位角相等,两直线平行进行填空即可.
9. 内错角相等,两直线平行
由图可知, 与 是一对内错角,且 ,
直线 (内错角相等,两直线平行).
故答案为:内错角相等,两直线平行.
【分析】这是一道阅读理解题。认真读题,发现其中的原理和依据:内错角相等,两直线平行.
三、解答题
10. 解: .
理由如下:
∵ 平分 ,
∴ ,
∵ ,
∴ ,
∴ .
【分析】 ,理由如下:根据角平分线的定义得出 , 又 ,故 , 根据内错角相等,二直线平行得出结论:。21cnjy.com
一、单选题
1.如图所示,在下列四组条件中,能判定AB∥CD的是( ??)
A.?∠1=∠2???????????????????B.?∠ABD=∠BDC???????????????????C.?∠3=∠4???????????????????D.?∠BAD+∠ABC=180°
2.如图所示,下列条件中,不能判断AD∥BC的是(?? )
A.?∠1=∠4??????????????????????B.?∠3=∠4??????????????????????C.?∠2+∠3=180°??????????????????????D.?∠1+∠D=180°
3.如图,不能作为判断AE∥CD的条件的是(??? )
A.?∠FEB=∠ECD??????????????B.?∠AEC=∠ECD??????????????C.?∠BEC+∠ECD=180°??????????????D.?∠AEG=∠DCH??
4.如图,下列能判定AB∥EF的条件有(?? )
①∠B+∠BFE=180°;②∠1=∠2;③∠3=∠4;④∠B=∠5.
A.?1个???????????????????????????????????????B.?2个???????????????????????????????????????C.?3个???????????????????????????????????????D.?4个
5.如图,能判断 的条件是(?? )
A.?????????????????????B.?????????????????????C.?????????????????????D.?以上都对
6.下列命题属于真命题的是(??? )
A.?同旁内角相等,两直线平行????????????????????????????????B.?相等的角是对顶角 C.?平行于同一条直线的两条直线平行??????????????????????D.?同位角相等21·cn·jy·com
7.下列图形中,由 ,能得到 的是(??? )
A.???????????????B.???????????????C.???????????????D.?
二、填空题
8.如图,若要 ,需增加条件________.(填一个即可)
9.阅读下面材料:在数学课上,老师提出如下问题:
作图:过直线外一点作已知直线的平行线.
已知:直线l及其外一点A(如图1).
求作:l的平行线,使它经过点A .
小凡利用两块形状相同的三角尺进行如下操作:
如图2所示:
⑴用第一块三角尺的一条边贴住直线l , 第二块三角尺的一条边紧靠第一块三角尺;
⑵将第二块三角尺沿第一块三角尺移动,使其另一边经过点A , 沿这边作出直线AB , 所以,直线AB即为所求.www.21-cn-jy.com
老师说:“小凡的作法正确”
请回答:小凡的作图依据是________.
三、解答题
10.已知:如图, 平分 , .那么 与 平行吗?请说明理由.
答案解析部分
一、单选题
1. B
解:A、∵∠1=∠2,∴ AD∥BC,不符合题意; B、??∵∠ABD=∠BDC?,∴AB∥CD,符合题意; C、∵ ∠3=∠4 ,∴ AD∥BC,不符合题意; D、∵ ∠BAD+∠ABC=180°?,∴AD∥BC,不符合题意; 故答案为:B. 【分析】根据平行线的性质,即同位角相等两直线平行,内错角相等两直线平行,同旁内角互补两直线平行,逐项分析判断即可.2·1·c·n·j·y
2. A
解:A、∵∠1=∠4,∴AB∥CD(内错角相等,两直线平行),但不能判定AD∥BC;
B、∵∠3=∠4,∴AD∥BC(同位角相等,两直线平行);
C、∵∠2+∠3=180°,∴AD∥BC(同旁内角互补,两直线平行);
D、∵∠1+∠D=180°,∴AD∥BC(同旁内角互补,两直线平行);
故答案为:A.
【分析】A、∠1与∠4是直线DC,AB被BC所截的一对内错角,根据内错角相等,二直线平行得出AB∥CD,但不能判定AD∥BC,A符合题意; B、∠3与∠4是直线DA,CB被BA所截的一对同位角,根据同位角相等,二直线平行得出AD∥CB,B不符合题意; C、∠3与∠2是直线DA,CB被BA所截的一对同旁内角,根据同旁内角互补,二直线平行得出AD∥CB,B不符合题意; D、∠1与∠D是直线DA,CB被DC所截的一对同旁内角,根据同旁内角互补,二直线平行得出AD∥CB,B不符合题意,综上所述就可得出答案.21教育网
3. D
解:A、 ∠FEB=∠ECD ,则AE∥CD(同位角相等两直线平行),正确,不符合题意; B、 ∠AEC=∠ECD ,则AE∥CD(内错角相等两直线平行),正确,不符合题意; C、 ∠BEC+∠ECD=180° ,则AE∥CD(同旁内角互补两直线平行),正确,不符合题意; D、 ∠AEG和∠DCH不属于三线八角当中的一组角,不能用来判断是否平行,错误,符合题意; 故答案为:D. 【分析】利用平行线的判定定理,即同位角相等两直线平行,内错角相等两直线平行,同旁内角互补两直线平行,逐一判断即可。【来源:21·世纪·教育·网】
4. C
解:当∠B+∠BFE=180°,AB∥EF;当∠1=∠2时,DE∥BC;当∠3=∠4时,AB∥EF;当∠B=∠5时,AB∥EF. 21·纪*教育网
故答案为:C.
【分析】根据同旁内角互补两直线平行可得AB∥EF;根据内错角相等两直线平行可得DE∥BC,AB∥EF;根据同位角相等两直线平行可得AB∥EF.据此判断即可.www-2-1-cnjy-com
5. B
解:A. 与 既不是同位角又不是内错角,因而A选项无法判断 ;
B选项:如图:
由因为∠1+∠6=180°,∠6=∠2;所以当∠1+∠2=180°时,所以AB//CD,故B符合.
C. 与 既不是同位角又不是内错角,因而C选项无法判断 ;
D选项也不对.
故答案为:B.
【分析】平行线的判定方法:同位角相等,两直线平行;内错角相等,两直线平行;同旁内角互补两直线平行;如图“三线八角”中,利用同角的补角相等可得∠6=∠2,利用同位角相等,两直线平行可得AB∥CD,据此判断即可.2-1-c-n-j-y
6. C
解:A、同旁内角互补,两直线平行,是假命题;
B、相等的角不一定是对顶角,是假命题;
C、平行于同一条直线的两条直线平行,是真命题;
D、两直线平行,同位角相等,是假命题。
故答案为:C。
【分析】根据平行线的判定方法,同旁内角互补,二直线平行;根据对顶角的性质,对顶角相等,但相等的角不一定是对顶角;根据平行线的传递性,平行于同一条直线的两条直线平行;根据平行线的性质,两直线平行,同位角相等,从而即可一一判断得出答案。21*cnjy*com
7. B
解:A.∵∠1=∠2是同旁内角,∴不能判断 ,故不符合题意;
B.作∠3如下图,
∵∠1=∠3,∠1=∠2,∴∠2=∠3,∴
故∠1=∠2,则 ,故符合题意;
C. ∠1=∠2可得 不能得到 ,故不符合题意;
D. ∠1=∠2不能得到 ,故不符合题意. 故答案为:B. 【分析】A、∠1=∠2是同旁内角,即使相等,也判断不出 ,故A不符合题意;
B、首先根据对顶角相等判断出∠1=∠3,再根据等量代换得出∠2=∠3,然后根据同位角相等,二直线平行得出, 故B正确,符合题意; C、根据内错角相等,二直线平行,由 ∠1=∠2可得 , 不能得到 ,故C错误,不符合题意; D、∠1=∠2是同旁内角,即使相等,也判断不出 ,故D错误,不符合题意。 ?21世纪教育网版权所有
二、填空题
8.
解: ,
(同位角相等,两直线平行),
故答案为: .
【分析】根据同位角相等,两直线平行进行填空即可.
9. 内错角相等,两直线平行
由图可知, 与 是一对内错角,且 ,
直线 (内错角相等,两直线平行).
故答案为:内错角相等,两直线平行.
【分析】这是一道阅读理解题。认真读题,发现其中的原理和依据:内错角相等,两直线平行.
三、解答题
10. 解: .
理由如下:
∵ 平分 ,
∴ ,
∵ ,
∴ ,
∴ .
【分析】 ,理由如下:根据角平分线的定义得出 , 又 ,故 , 根据内错角相等,二直线平行得出结论:。21cnjy.com
同课章节目录
- 第1章 走进数学世界
- 数学伴我们成长
- 人类离不开数学
- 人人都能学会数学
- 第2章 有理数
- 2.1 有理数
- 2.2 数轴
- 2.3 相反数
- 2.4 绝对值
- 2.5 有理数的大小比较
- 2.6 有理数的加法
- 2.7 有理数的减法
- 2.8 有理数加减混合运算
- 2.9 有理数的乘法
- 2.10 有理数的除法
- 2.11 有理数的乘方
- 2.12 科学记数法
- 2.13 有理数的混合运算
- 2.14 近似数
- 2.15 用计算器进行计算
- 第3章 整式的加减
- 3.1 列代数式
- 3.2 代数式的值
- 3.3 整式
- 3.4 整式的加减
- 第4章 图形的初步认识
- 4.1 生活中的立体图形
- 4.2 立体图形的视图
- 4.3 立体图形的表面展开图
- 4.4 平面图形
- 4.5 最基本的图形——点和线
- 4.6 角
- 第5章 相交线与平行线
- 5.1 相交线
- 5.2 平行线
