人教版八年级上数学教学讲义,复习补习资料(含知识讲解,巩固练习):22作轴对称图形含答案
文档属性
| 名称 | 人教版八年级上数学教学讲义,复习补习资料(含知识讲解,巩固练习):22作轴对称图形含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 195.8KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-03 07:46:41 | ||
图片预览


文档简介
作轴对称图形 知识讲解
【学习目标】
1.理解轴对称变换,能作出已知图形关于某条直线的对称图形.
2.能利用轴对称变换,设计一些图案,解决简单的实际问题.
3.运用所学的轴对称知识,认识和掌握在平面直角坐标系中,与已知点关于x轴或y轴对称点的坐标的规律,进而能在平面直角坐标系中作出与一个图形关于x轴或y轴对称的图形.
4.能运用轴对称的性质,解决简单的数学问题或实际问题,提高分析问题和解决问题的能力.
【要点梳理】
要点一、对称轴的作法 若两个图形成轴对称,其对称轴就是任何一对对应点所连线段的垂直平分线.因此只要找到一对对应点,再作出连接它们的线段的垂直平分线就可以得到这两个图形的对称轴.轴对称图形的对称轴作法相同.
要点诠释:
在轴对称图形和成轴对称的两个图形中,对应线段、对应角相等.成轴对称的两个图形,如果它们的对应线段或延长线相交,那么交点一定在对称轴上.如果两个图形的对应点连线被同一条直线垂直平分,那么这两个图形关于这条直线对称.
【 作轴对称图形,用坐标表示轴对称】
要点二、 用坐标表示轴对称 1.关于x轴对称的两个点的横(纵)坐标的关系 已知P点坐标,则它关于轴的对称点的坐标为,如下图所示:
即关于轴的对称的两点,坐标的关系是:横坐标相同,纵坐标互为相反数. 2.关于y轴对称的两个点横(纵)坐标的关系 已知P点坐标为,则它关于轴对称点的坐标为,如上图所示. 即关于轴对称的两点坐标关系是:纵坐标相同,横坐标互为相反数. 3.关于与x轴(y轴)平行的直线对称的两个点横(纵)坐标的关系 P点坐标关于直线的对称点的坐标为.
P点坐标关于直线的对称点的坐标为.
【典型例题】
类型一、作轴对称图形
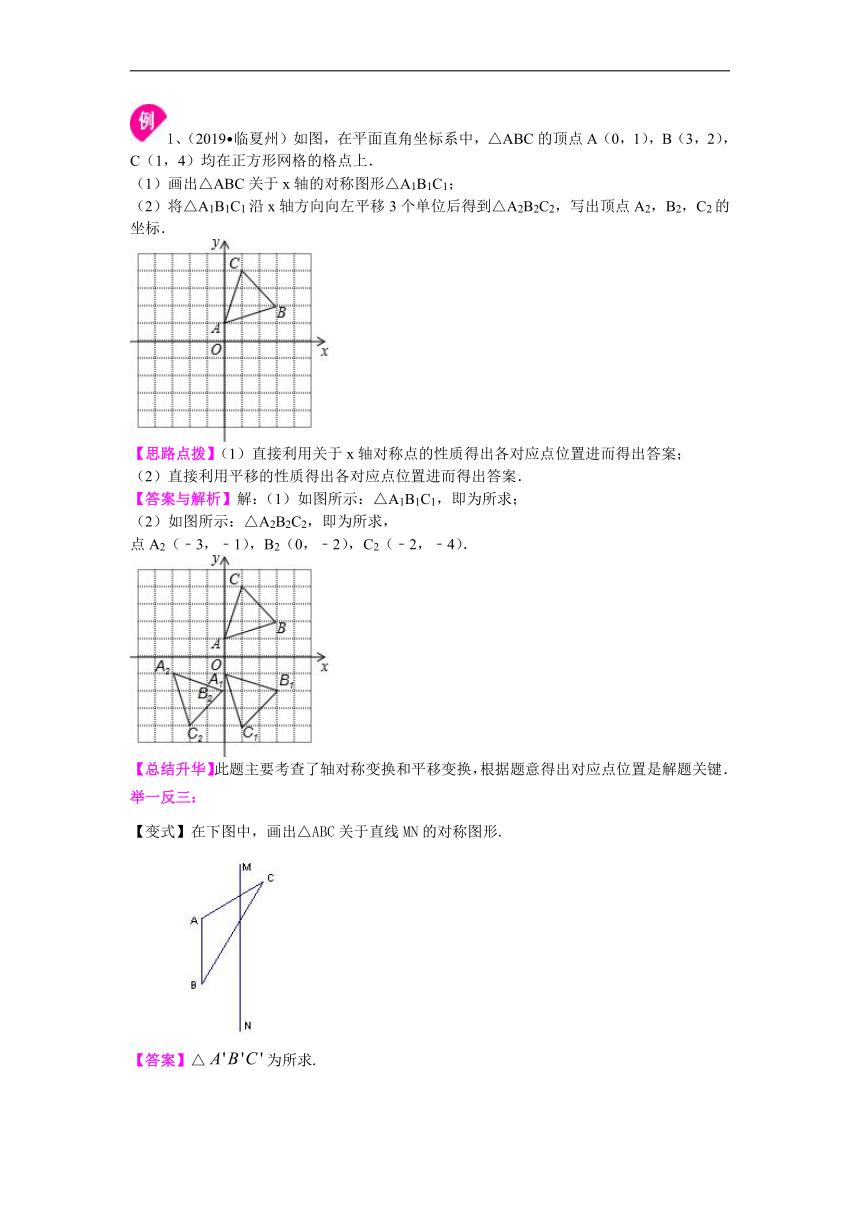
1、(2019?临夏州)如图,在平面直角坐标系中,△ABC的顶点A(0,1),B(3,2),C(1,4)均在正方形网格的格点上.
(1)画出△ABC关于x轴的对称图形△A1B1C1;
(2)将△A1B1C1沿x轴方向向左平移3个单位后得到△A2B2C2,写出顶点A2,B2,C2的坐标.
【思路点拨】(1)直接利用关于x轴对称点的性质得出各对应点位置进而得出答案;
(2)直接利用平移的性质得出各对应点位置进而得出答案.
【答案与解析】解:(1)如图所示:△A1B1C1,即为所求;
(2)如图所示:△A2B2C2,即为所求,
点A2(﹣3,﹣1),B2(0,﹣2),C2(﹣2,﹣4).
【总结升华】此题主要考查了轴对称变换和平移变换,根据题意得出对应点位置是解题关键.
举一反三:
【变式】在下图中,画出△ABC关于直线MN的对称图形.
【答案】△为所求.
类型二、轴对称变换的应用(将军饮马问题)
【 作轴对称图形,例4】
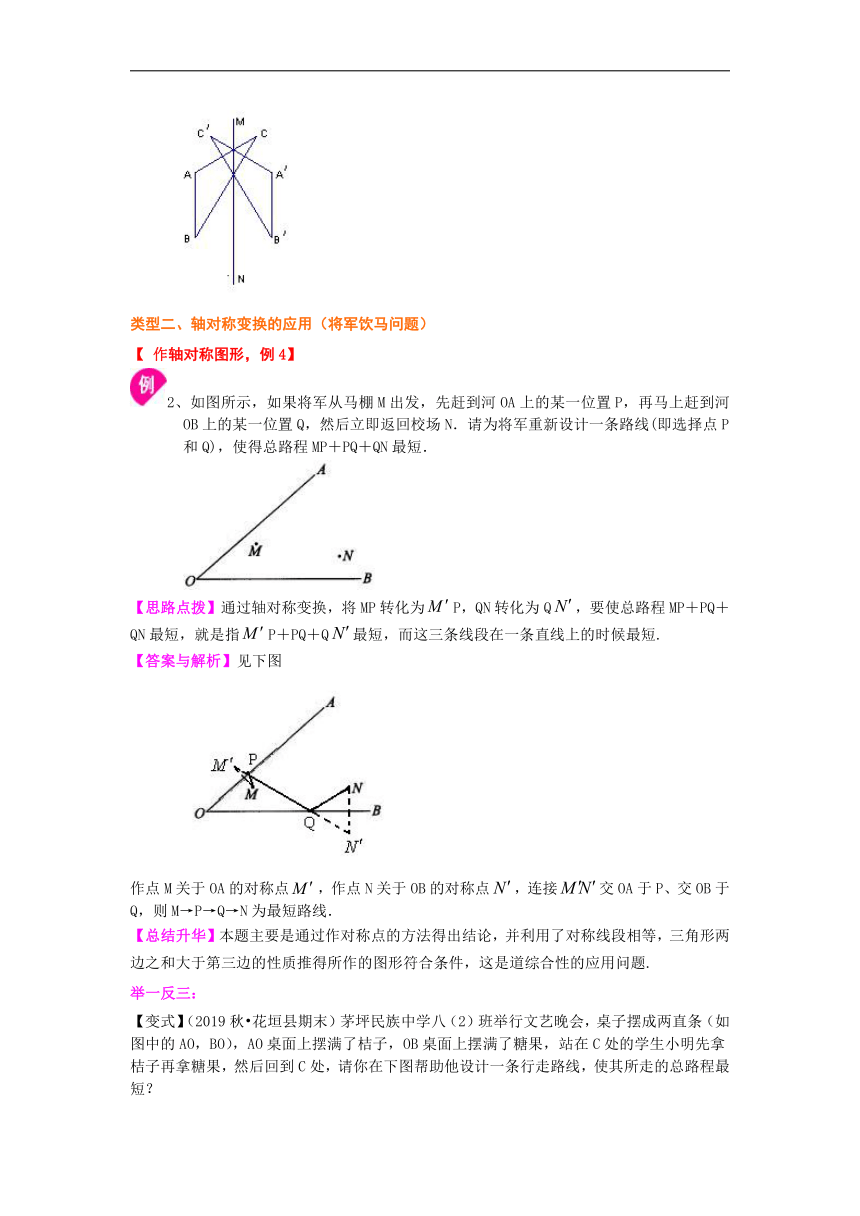
2、如图所示,如果将军从马棚M出发,先赶到河OA上的某一位置P,再马上赶到河OB上的某一位置Q,然后立即返回校场N.请为将军重新设计一条路线(即选择点P和Q),使得总路程MP+PQ+QN最短.
【思路点拨】通过轴对称变换,将MP转化为P,QN转化为Q,要使总路程MP+PQ+QN最短,就是指P+PQ+Q最短,而这三条线段在一条直线上的时候最短.
【答案与解析】见下图
作点M关于OA的对称点,作点N关于OB的对称点,连接交OA于P、交OB于Q,则M→P→Q→N为最短路线.
【总结升华】本题主要是通过作对称点的方法得出结论,并利用了对称线段相等,三角形两边之和大于第三边的性质推得所作的图形符合条件,这是道综合性的应用问题.
举一反三:
【变式】(2019秋?花垣县期末)茅坪民族中学八(2)班举行文艺晚会,桌子摆成两直条(如图中的AO,BO),AO桌面上摆满了桔子,OB桌面上摆满了糖果,站在C处的学生小明先拿桔子再拿糖果,然后回到C处,请你在下图帮助他设计一条行走路线,使其所走的总路程最短?
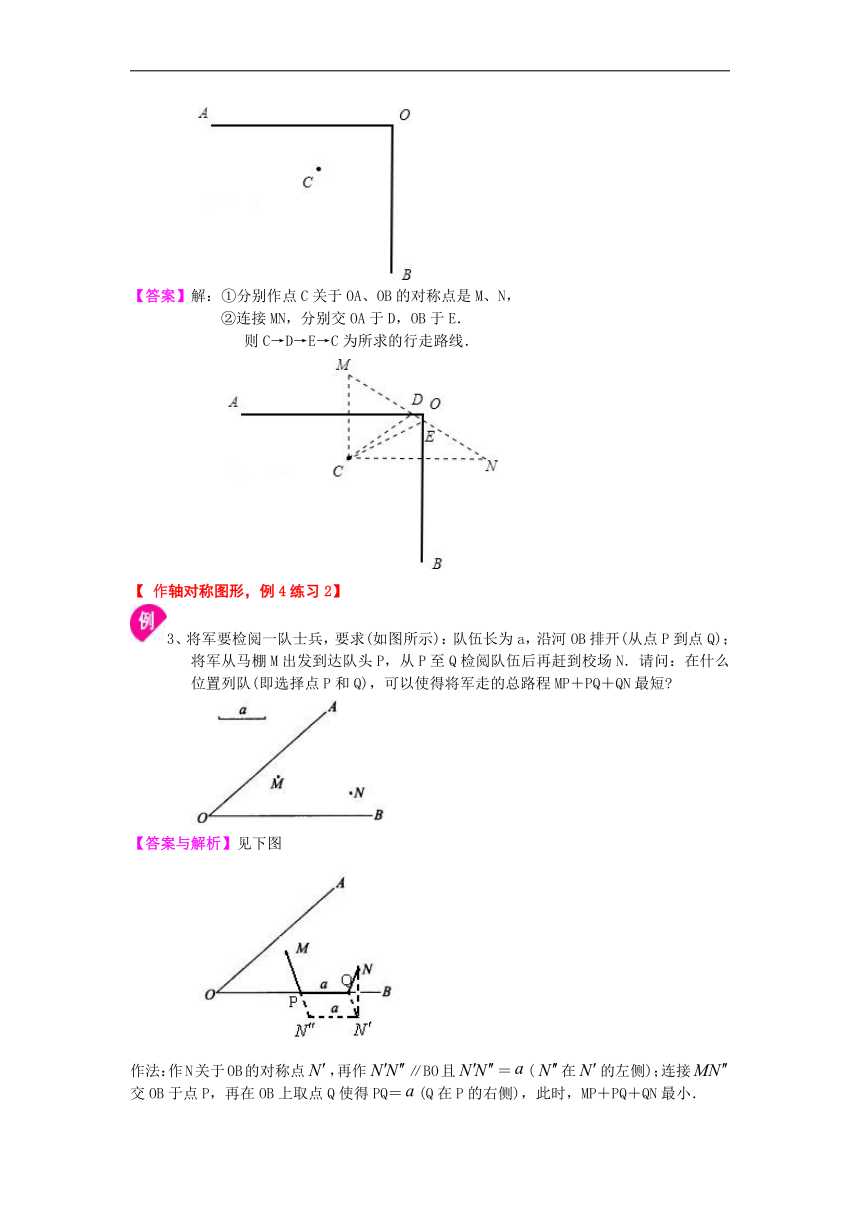
【答案】解:①分别作点C关于OA、OB的对称点是M、N,
②连接MN,分别交OA于D,OB于E.
则C→D→E→C为所求的行走路线.
【 作轴对称图形,例4练习2】
3、将军要检阅一队士兵,要求(如图所示):队伍长为a,沿河OB排开(从点P到点Q);将军从马棚M出发到达队头P,从P至Q检阅队伍后再赶到校场N.请问:在什么位置列队(即选择点P和Q),可以使得将军走的总路程MP+PQ+QN最短?
【答案与解析】见下图
作法:作N关于OB的对称点,再作∥BO且=(在的左侧);连接交OB于点P,再在OB上取点Q使得PQ=(Q在P的右侧),此时,MP+PQ+QN最小.
【总结升华】MP+PQ+QN最小,其中PQ是定值,问题转化为MP+QN最小.因为将军要沿河走一段线段,如果能把这段提前走掉就可以转化为熟悉的问题了,于是考虑从沿平行的方向走至,连接即可.
类型三、用坐标表示轴对称
4、(2019秋?江津区期中)已知点A(2a﹣b,5+a),B(2b﹣1,﹣a+b).
(1)若点A、B关于x轴对称,求a、b的值;
(2)若A、B关于y轴对称,求﹙4a+b﹚2019的值.
【思路点拨】
(1)根据关于x轴对称点的坐标特点:横坐标不变,纵坐标互为相反数可得2a﹣b=2b﹣1,5+a﹣a+b=0,解可得a、b的值;
(2)根据关于y轴对称点的坐标特点:横坐标互为相反数,纵坐标不变可得2a﹣b+2b﹣1=0,5+a=﹣a+b,解出a、b的值,进而可得答案.
【答案与解析】
解:(1)∵点A、B关于x轴对称,
∴2a﹣b=2b﹣1,5+a﹣a+b=0,
解得:a=﹣8,b=﹣5;
(2)∵A、B关于y轴对称,
∴2a﹣b+2b﹣1=0,5+a=﹣a+b,
解得:a=﹣1,b=3,
﹙4a+b﹚2019=1.
【总结升华】此题主要考查了关于x、y轴对称的点的坐标,关键是掌握点的坐标的变化规律.
举一反三:
【变式1】已知点A(,)关于轴对称的点的坐标为点B(,),则的值为( ).
A. B. C. D.
【答案】B;
提示:2=2,+=3, 解得=2, =1,选B.
【变式2】如图,ΔABC中,点A的坐标为(0,1),点C的坐标为(4,3),点B的坐标为(3,1),如果要使ΔABD与ΔABC全等,求点D的坐标.
【答案】共3个满足条件的点:(4,-1),(-1,3),(-1,-1).
【巩固练习】
一.选择题
1. 下列说法中,正确的是( )
A.关于某直线对称的两个三角形是全等三角形
B.全等三角形是关于某直线对称的
C.两个图形关于某条直线对称,这两个图形一定分别位于这条直线的两侧
D.若点A、B关于直线MN对称,则AB垂直平分MN
2.(2019春?岳池县期末)如果点A(x﹣y,x+y)与点B(5,﹣3)关于y轴对称,那么x,y的值是( )
A.x=4,y=﹣1 B.x=﹣4,y=﹣1 C.x=4,y=1 D.x=﹣4,y=1
3. 如图,△ABC与△关于直线MN对称,P为MN上任一点,下列结论中错误的是( )
A.△是等腰三角形 B.MN垂直平分,
C.△ABC与△面积相等 D.直线AB、的交点不一定在MN上
4. 已知点(,5)与(2,-1)关于轴的对称,则的值为( )
A.0 B.-1 C.1 D.
5. (2019?赤峰)平面直角坐标系内的点A(﹣1,2)与点B(﹣1,﹣2)关于( )
A.y轴对称 B.x轴对称 C.原点对称 D.直线y=x对称
6. 如图,六边形ABCDEF是轴对称图形,CF所在的直线是它的对称轴,若∠AFC+∠BCF
=150°,则∠AFE+∠BCD的大小是( )
A.150° B.300° C.210° D.330°
二.填空题
7. 已知△ABC和△关于MN对称,并且AB=5,BC=3,则的取值范围是_________.
8. 已知点A(,2),B(-3,).若A,B关于轴对称,则=_____,=_____.若A,B关于轴对称,则=_____,=_________.
9. 若点P(,)关于轴的对称点是,关于轴对称点为,且坐标为(-3,4)则=________,=_______.
10.(2019?南京)在平面直角坐标系中,点A的坐标是(2,﹣3),作点A关于x轴的对称点,得到点A′,再作点A′关于y轴的对称点,得到点A″,则点A″的坐标是( , ).
11. 如图,这是小龙制作的风筝,为了平衡做成轴对称图形,已知OC所在的直线为对称轴,且∠A=32°,∠ACO=24°,则∠BOC=________.
12. (2019?富顺县校级模拟)平面直角坐标系中的点P关于x轴的对称点在第四象限,则m的取值范围为 .
三.解答题
13. 如图,在正方形网格中,阴影部分是由5个小正方形组成的一个图形,请你用两种方法分别在下图方格内添涂2个小正方形,使这7个小正方形组成的图形是轴对称图形.
14. 如图,点M在锐角∠AOB内部,在OB边上求作一点P,使点P到点M的距离与点P到OA边的距离之和最小
15. (2019春?沙坪坝区期末)如图所示的正方形网格中,每个小正方形的边长均为1个单位,△ABC的三个顶点都在格点上.
(1)在网格中画出△ABC向下平移3个单位得到的△A1B1C1;
(2)在网格中画出△A1B1C1关于直线m对称的△A2B2C2;
(3)在直线m上画一点P,使得C1P+C2P的值最小.
【答案与解析】
一.选择题
1. 【答案】A;
【解析】C项这两个图形有可能相交,D项是MN垂直平分AB.
2. 【答案】D;
【解析】解:∵点A(x﹣y,x+y)与点B(5,﹣3)关于y轴对称,
∴,解得:,
故选:D.
3. 【答案】D ;
【解析】对应线段所在直线的交点一定在对称轴上或平行于对称轴.
4. 【答案】B;
【解析】=3, =-4, +=-1.
5. 【答案】B;
6. 【答案】B;
【解析】对称轴两边的图形全等,∠AFE+∠BCD=2(∠AFC+∠BCF)=300°.
二.填空题
7. 【答案】2<<8;
【解析】△ABC和△关于MN对称,∴△ABC≌△,大于两边之差,小于两边之和.
8. 【答案】-3,-2; 3, 2;
【解析】关于轴对称的点横坐标一样,纵坐标相反;关于轴对称的点,横坐标相反,纵坐标一样.
9. 【答案】3,-4;
【解析】(-3,-4),P(3,-4).
10.【答案】-2,3;
【解析】解:∵点A的坐标是(2,﹣3),作点A关于x轴的对称点,得到点A′,
∴A′的坐标为:(2,3),
∵点A′关于y轴的对称点,得到点A″,
∴点A″的坐标是:(﹣2,3).
故答案为:﹣2;3.
11.【答案】124°;
【解析】成轴对称的图形全等,∠BOC=180°-32°-24°=124°.
12.【答案】0<m<2;
【解析】∵P1(2﹣m,﹣m)在第四象限,∴,解得0<m<2,
∴m的取值范围为 0<m<2.
三.解答题
13.【解析】
答案不唯一,参见下图.
14.【解析】
作法如下:
作M点关于OB的对称点,过作⊥于OA于H,交OB于P,点P为所求.
15.【解析】
解:(1)如图,△A1B1C1即为所求;
(2)如图,△A2B2C2即为所求;
(3)连接C1C2交直线m于点P,则点P即为所求点.
【学习目标】
1.理解轴对称变换,能作出已知图形关于某条直线的对称图形.
2.能利用轴对称变换,设计一些图案,解决简单的实际问题.
3.运用所学的轴对称知识,认识和掌握在平面直角坐标系中,与已知点关于x轴或y轴对称点的坐标的规律,进而能在平面直角坐标系中作出与一个图形关于x轴或y轴对称的图形.
4.能运用轴对称的性质,解决简单的数学问题或实际问题,提高分析问题和解决问题的能力.
【要点梳理】
要点一、对称轴的作法 若两个图形成轴对称,其对称轴就是任何一对对应点所连线段的垂直平分线.因此只要找到一对对应点,再作出连接它们的线段的垂直平分线就可以得到这两个图形的对称轴.轴对称图形的对称轴作法相同.
要点诠释:
在轴对称图形和成轴对称的两个图形中,对应线段、对应角相等.成轴对称的两个图形,如果它们的对应线段或延长线相交,那么交点一定在对称轴上.如果两个图形的对应点连线被同一条直线垂直平分,那么这两个图形关于这条直线对称.
【 作轴对称图形,用坐标表示轴对称】
要点二、 用坐标表示轴对称 1.关于x轴对称的两个点的横(纵)坐标的关系 已知P点坐标,则它关于轴的对称点的坐标为,如下图所示:
即关于轴的对称的两点,坐标的关系是:横坐标相同,纵坐标互为相反数. 2.关于y轴对称的两个点横(纵)坐标的关系 已知P点坐标为,则它关于轴对称点的坐标为,如上图所示. 即关于轴对称的两点坐标关系是:纵坐标相同,横坐标互为相反数. 3.关于与x轴(y轴)平行的直线对称的两个点横(纵)坐标的关系 P点坐标关于直线的对称点的坐标为.
P点坐标关于直线的对称点的坐标为.
【典型例题】
类型一、作轴对称图形
1、(2019?临夏州)如图,在平面直角坐标系中,△ABC的顶点A(0,1),B(3,2),C(1,4)均在正方形网格的格点上.
(1)画出△ABC关于x轴的对称图形△A1B1C1;
(2)将△A1B1C1沿x轴方向向左平移3个单位后得到△A2B2C2,写出顶点A2,B2,C2的坐标.
【思路点拨】(1)直接利用关于x轴对称点的性质得出各对应点位置进而得出答案;
(2)直接利用平移的性质得出各对应点位置进而得出答案.
【答案与解析】解:(1)如图所示:△A1B1C1,即为所求;
(2)如图所示:△A2B2C2,即为所求,
点A2(﹣3,﹣1),B2(0,﹣2),C2(﹣2,﹣4).
【总结升华】此题主要考查了轴对称变换和平移变换,根据题意得出对应点位置是解题关键.
举一反三:
【变式】在下图中,画出△ABC关于直线MN的对称图形.
【答案】△为所求.
类型二、轴对称变换的应用(将军饮马问题)
【 作轴对称图形,例4】
2、如图所示,如果将军从马棚M出发,先赶到河OA上的某一位置P,再马上赶到河OB上的某一位置Q,然后立即返回校场N.请为将军重新设计一条路线(即选择点P和Q),使得总路程MP+PQ+QN最短.
【思路点拨】通过轴对称变换,将MP转化为P,QN转化为Q,要使总路程MP+PQ+QN最短,就是指P+PQ+Q最短,而这三条线段在一条直线上的时候最短.
【答案与解析】见下图
作点M关于OA的对称点,作点N关于OB的对称点,连接交OA于P、交OB于Q,则M→P→Q→N为最短路线.
【总结升华】本题主要是通过作对称点的方法得出结论,并利用了对称线段相等,三角形两边之和大于第三边的性质推得所作的图形符合条件,这是道综合性的应用问题.
举一反三:
【变式】(2019秋?花垣县期末)茅坪民族中学八(2)班举行文艺晚会,桌子摆成两直条(如图中的AO,BO),AO桌面上摆满了桔子,OB桌面上摆满了糖果,站在C处的学生小明先拿桔子再拿糖果,然后回到C处,请你在下图帮助他设计一条行走路线,使其所走的总路程最短?
【答案】解:①分别作点C关于OA、OB的对称点是M、N,
②连接MN,分别交OA于D,OB于E.
则C→D→E→C为所求的行走路线.
【 作轴对称图形,例4练习2】
3、将军要检阅一队士兵,要求(如图所示):队伍长为a,沿河OB排开(从点P到点Q);将军从马棚M出发到达队头P,从P至Q检阅队伍后再赶到校场N.请问:在什么位置列队(即选择点P和Q),可以使得将军走的总路程MP+PQ+QN最短?
【答案与解析】见下图
作法:作N关于OB的对称点,再作∥BO且=(在的左侧);连接交OB于点P,再在OB上取点Q使得PQ=(Q在P的右侧),此时,MP+PQ+QN最小.
【总结升华】MP+PQ+QN最小,其中PQ是定值,问题转化为MP+QN最小.因为将军要沿河走一段线段,如果能把这段提前走掉就可以转化为熟悉的问题了,于是考虑从沿平行的方向走至,连接即可.
类型三、用坐标表示轴对称
4、(2019秋?江津区期中)已知点A(2a﹣b,5+a),B(2b﹣1,﹣a+b).
(1)若点A、B关于x轴对称,求a、b的值;
(2)若A、B关于y轴对称,求﹙4a+b﹚2019的值.
【思路点拨】
(1)根据关于x轴对称点的坐标特点:横坐标不变,纵坐标互为相反数可得2a﹣b=2b﹣1,5+a﹣a+b=0,解可得a、b的值;
(2)根据关于y轴对称点的坐标特点:横坐标互为相反数,纵坐标不变可得2a﹣b+2b﹣1=0,5+a=﹣a+b,解出a、b的值,进而可得答案.
【答案与解析】
解:(1)∵点A、B关于x轴对称,
∴2a﹣b=2b﹣1,5+a﹣a+b=0,
解得:a=﹣8,b=﹣5;
(2)∵A、B关于y轴对称,
∴2a﹣b+2b﹣1=0,5+a=﹣a+b,
解得:a=﹣1,b=3,
﹙4a+b﹚2019=1.
【总结升华】此题主要考查了关于x、y轴对称的点的坐标,关键是掌握点的坐标的变化规律.
举一反三:
【变式1】已知点A(,)关于轴对称的点的坐标为点B(,),则的值为( ).
A. B. C. D.
【答案】B;
提示:2=2,+=3, 解得=2, =1,选B.
【变式2】如图,ΔABC中,点A的坐标为(0,1),点C的坐标为(4,3),点B的坐标为(3,1),如果要使ΔABD与ΔABC全等,求点D的坐标.
【答案】共3个满足条件的点:(4,-1),(-1,3),(-1,-1).
【巩固练习】
一.选择题
1. 下列说法中,正确的是( )
A.关于某直线对称的两个三角形是全等三角形
B.全等三角形是关于某直线对称的
C.两个图形关于某条直线对称,这两个图形一定分别位于这条直线的两侧
D.若点A、B关于直线MN对称,则AB垂直平分MN
2.(2019春?岳池县期末)如果点A(x﹣y,x+y)与点B(5,﹣3)关于y轴对称,那么x,y的值是( )
A.x=4,y=﹣1 B.x=﹣4,y=﹣1 C.x=4,y=1 D.x=﹣4,y=1
3. 如图,△ABC与△关于直线MN对称,P为MN上任一点,下列结论中错误的是( )
A.△是等腰三角形 B.MN垂直平分,
C.△ABC与△面积相等 D.直线AB、的交点不一定在MN上
4. 已知点(,5)与(2,-1)关于轴的对称,则的值为( )
A.0 B.-1 C.1 D.
5. (2019?赤峰)平面直角坐标系内的点A(﹣1,2)与点B(﹣1,﹣2)关于( )
A.y轴对称 B.x轴对称 C.原点对称 D.直线y=x对称
6. 如图,六边形ABCDEF是轴对称图形,CF所在的直线是它的对称轴,若∠AFC+∠BCF
=150°,则∠AFE+∠BCD的大小是( )
A.150° B.300° C.210° D.330°
二.填空题
7. 已知△ABC和△关于MN对称,并且AB=5,BC=3,则的取值范围是_________.
8. 已知点A(,2),B(-3,).若A,B关于轴对称,则=_____,=_____.若A,B关于轴对称,则=_____,=_________.
9. 若点P(,)关于轴的对称点是,关于轴对称点为,且坐标为(-3,4)则=________,=_______.
10.(2019?南京)在平面直角坐标系中,点A的坐标是(2,﹣3),作点A关于x轴的对称点,得到点A′,再作点A′关于y轴的对称点,得到点A″,则点A″的坐标是( , ).
11. 如图,这是小龙制作的风筝,为了平衡做成轴对称图形,已知OC所在的直线为对称轴,且∠A=32°,∠ACO=24°,则∠BOC=________.
12. (2019?富顺县校级模拟)平面直角坐标系中的点P关于x轴的对称点在第四象限,则m的取值范围为 .
三.解答题
13. 如图,在正方形网格中,阴影部分是由5个小正方形组成的一个图形,请你用两种方法分别在下图方格内添涂2个小正方形,使这7个小正方形组成的图形是轴对称图形.
14. 如图,点M在锐角∠AOB内部,在OB边上求作一点P,使点P到点M的距离与点P到OA边的距离之和最小
15. (2019春?沙坪坝区期末)如图所示的正方形网格中,每个小正方形的边长均为1个单位,△ABC的三个顶点都在格点上.
(1)在网格中画出△ABC向下平移3个单位得到的△A1B1C1;
(2)在网格中画出△A1B1C1关于直线m对称的△A2B2C2;
(3)在直线m上画一点P,使得C1P+C2P的值最小.
【答案与解析】
一.选择题
1. 【答案】A;
【解析】C项这两个图形有可能相交,D项是MN垂直平分AB.
2. 【答案】D;
【解析】解:∵点A(x﹣y,x+y)与点B(5,﹣3)关于y轴对称,
∴,解得:,
故选:D.
3. 【答案】D ;
【解析】对应线段所在直线的交点一定在对称轴上或平行于对称轴.
4. 【答案】B;
【解析】=3, =-4, +=-1.
5. 【答案】B;
6. 【答案】B;
【解析】对称轴两边的图形全等,∠AFE+∠BCD=2(∠AFC+∠BCF)=300°.
二.填空题
7. 【答案】2<<8;
【解析】△ABC和△关于MN对称,∴△ABC≌△,大于两边之差,小于两边之和.
8. 【答案】-3,-2; 3, 2;
【解析】关于轴对称的点横坐标一样,纵坐标相反;关于轴对称的点,横坐标相反,纵坐标一样.
9. 【答案】3,-4;
【解析】(-3,-4),P(3,-4).
10.【答案】-2,3;
【解析】解:∵点A的坐标是(2,﹣3),作点A关于x轴的对称点,得到点A′,
∴A′的坐标为:(2,3),
∵点A′关于y轴的对称点,得到点A″,
∴点A″的坐标是:(﹣2,3).
故答案为:﹣2;3.
11.【答案】124°;
【解析】成轴对称的图形全等,∠BOC=180°-32°-24°=124°.
12.【答案】0<m<2;
【解析】∵P1(2﹣m,﹣m)在第四象限,∴,解得0<m<2,
∴m的取值范围为 0<m<2.
三.解答题
13.【解析】
答案不唯一,参见下图.
14.【解析】
作法如下:
作M点关于OB的对称点,过作⊥于OA于H,交OB于P,点P为所求.
15.【解析】
解:(1)如图,△A1B1C1即为所求;
(2)如图,△A2B2C2即为所求;
(3)连接C1C2交直线m于点P,则点P即为所求点.
