人教版八年级上数学教学讲义,复习补习资料(含知识讲解,巩固练习):21轴对称含答案
文档属性
| 名称 | 人教版八年级上数学教学讲义,复习补习资料(含知识讲解,巩固练习):21轴对称含答案 |

|
|
| 格式 | zip | ||
| 文件大小 | 284.9KB | ||
| 资源类型 | 教案 | ||
| 版本资源 | 人教版 | ||
| 科目 | 数学 | ||
| 更新时间 | 2019-12-03 00:00:00 | ||
图片预览


文档简介
轴对称
【学习目标】
1.理解轴对称图形以及两个图形成轴对称的概念,弄清它们之间的区别与联系,能识别轴对称图形.
2.理解图形成轴对称的性质,会画一些简单的关于某直线对称的图形.
3.理解线段的垂直平分线的概念,掌握线段的垂直平分线的性质及判定,会画已知线段的垂直平分线.
4.能运用线段的垂直平分线的性质解决简单的数学问题及实际问题.
【要点梳理】
【 轴对称 知识要点】
要点一、轴对称图形 轴对称图形的定义
一个图形沿着某直线折叠,直线两旁的部分能完全重合,这个图形就叫做轴对称图形,该直线就是它的对称轴.
要点诠释: 轴对称图形是指一个图形,图形被对称轴分成的两部分能够互相重合.一个轴对称图形的对称轴不一定只有一条,也可能有两条或多条,因图形而定. 要点二、轴对称 1.轴对称定义
把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称(或说这两个图形成轴对称),这条直线叫做对称轴.折叠后重合的点是对应点,也叫做对称点 要点诠释: 轴对称指的是两个图形的位置关系,两个图形沿着某条直线对折后能够完全重合.成轴对称的两个图形一定全等.
2.轴对称与轴对称图形的区别与联系
轴对称与轴对称图形的区别主要是:轴对称是指两个图形,而轴对称图形是一个图形;轴对称图形和轴对称的关系非常密切,若把成轴对称的两个图形看作一个整体,则这个整体就是轴对称图形;反过来,若把轴对称图形的对称轴两旁的部分看作两个图形,则这两个图形关于这条直线(原对称轴)对称.
要点三、轴对称与轴对称图形的性质
轴对称、轴对称图形的性质 轴对称的性质:若两个图形关于某直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线;
轴对称图形的性质:轴对称图形的对称轴也是任何一对对应点所连线段的垂直平分线.
要点四、线段的垂直平分线
定义:
经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线,也叫线段的中垂线.
性质:
性质1:线段垂直平分线上的点到线段两端点的距离相等; 性质2:与一条线段两个端点距离相等的点在这条线段的垂直平分线上.
要点诠释:
线段的垂直平分线的性质是证明两线段相等的常用方法之一.同时也给出了引辅助线的方法,那就是遇见线段的垂直平分线,画出到线段两个端点的距离,这样就出现相等线段,直接或间接地为构造全等三角形创造条件.
三角形三边垂直平分线交于一点,该点到三角形三顶点的距离相等,这点是三角形外接圆的圆心——外心.
【典型例题】
类型一、判断轴对称图形
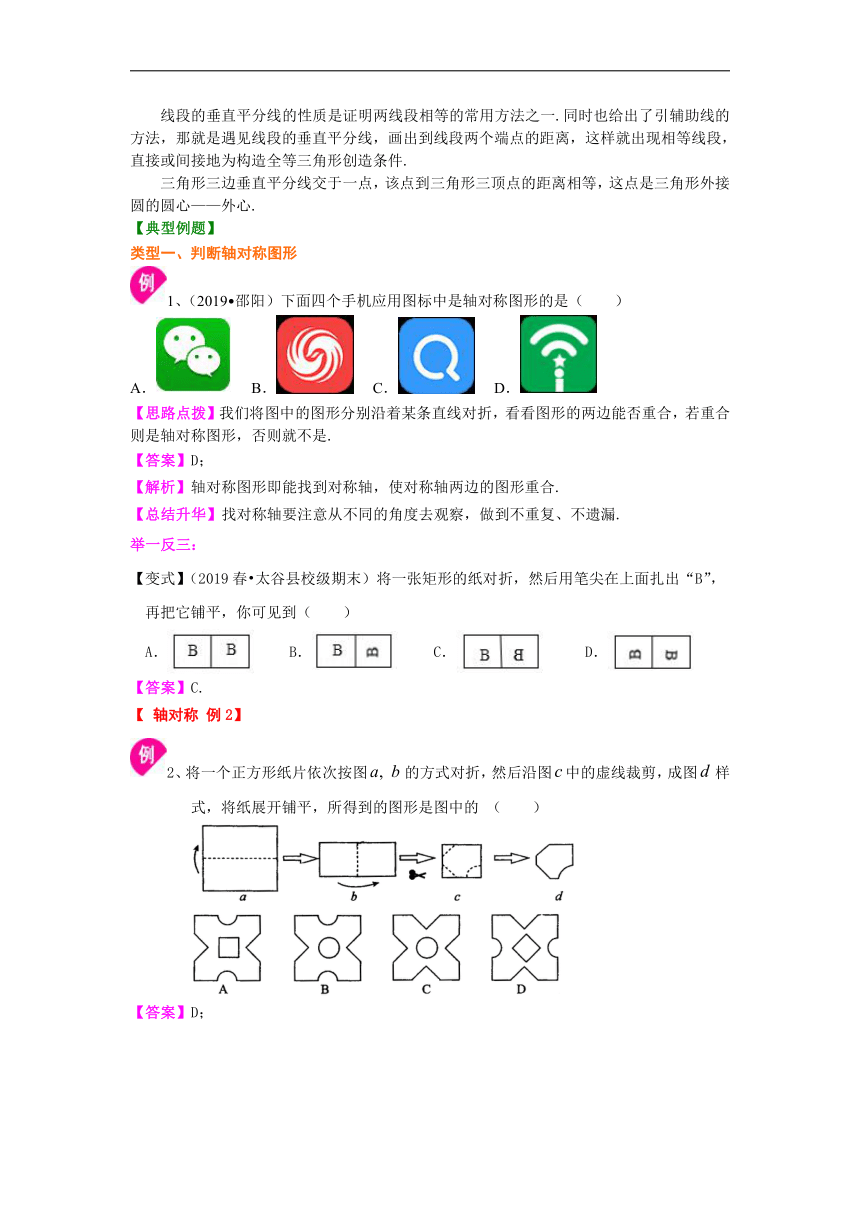
/1、(2019?邵阳)下面四个手机应用图标中是轴对称图形的是( )
A./ B./ C./ D./
【思路点拨】我们将图中的图形分别沿着某条直线对折,看看图形的两边能否重合,若重合则是轴对称图形,否则就不是.
【答案】D;
【解析】轴对称图形即能找到对称轴,使对称轴两边的图形重合.
【总结升华】找对称轴要注意从不同的角度去观察,做到不重复、不遗漏.
举一反三:
【变式】(2019春?太谷县校级期末)将一张矩形的纸对折,然后用笔尖在上面扎出“B”,再把它铺平,你可见到( )
A./ B./ C./ D./
【答案】C.
【 轴对称 例2】
/2、将一个正方形纸片依次按图/的方式对折,然后沿图/中的虚线裁剪,成图/样式,将纸展开铺平,所得到的图形是图中的 ( )
/
/
【答案】D;
【解析】/
【总结升华】只需要根据对称轴补全图形就能找到答案.
举一反三:
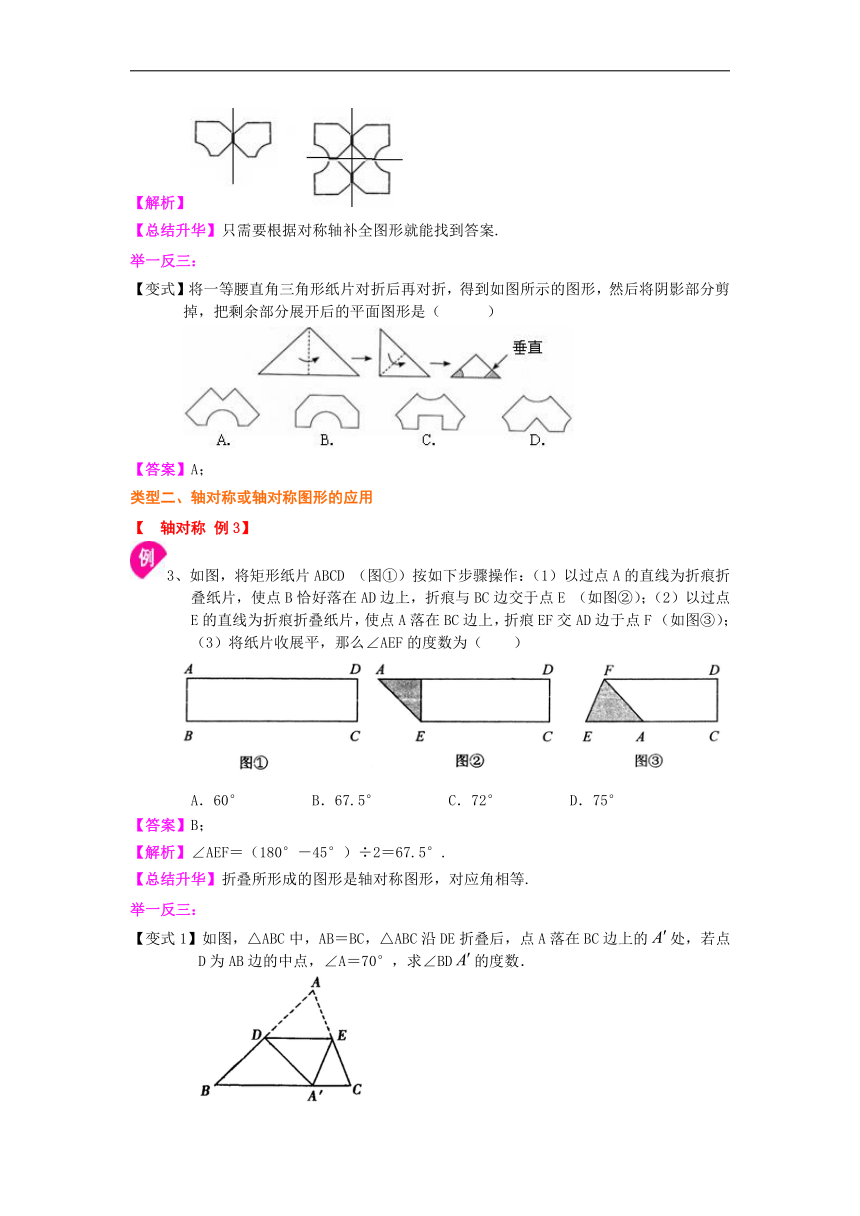
【变式】将一等腰直角三角形纸片对折后再对折,得到如图所示的图形,然后将阴影部分剪掉,把剩余部分展开后的平面图形是( )
/
【答案】A;
类型二、轴对称或轴对称图形的应用
【 轴对称 例3】
/3、如图,将矩形纸片ABCD (图①)按如下步骤操作:(1)以过点A的直线为折痕折叠纸片,使点B恰好落在AD边上,折痕与BC边交于点E (如图②);(2)以过点E的直线为折痕折叠纸片,使点A落在BC边上,折痕EF交AD边于点F (如图③); (3)将纸片收展平,那么∠AEF的度数为( )
/
A.60° B.67.5° C.72° D.75°
【答案】B;
【解析】∠AEF=(180°-45°)÷2=67.5°.
【总结升华】折叠所形成的图形是轴对称图形,对应角相等.
举一反三:
【变式1】如图,△ABC中,AB=BC,△ABC沿DE折叠后,点A落在BC边上的/处,若点D为AB边的中点,∠A=70°,求∠BD/的度数.
/
【答案】100°;
∵AB=BC,
∴∠A=∠C=70°,∠B=40°
又∵ΔABC沿DE折叠后,点A落在BC边上的/处,点D为AB边的中点,
∴BD=D/,∠B=∠D/B=40°,
∴∠BD/=180°-40°-40°=100°.
【变式2】将矩形ABCD沿AE折叠,得到如图所示图形. 若/=56°,则∠AED的大小是_______.
/
【答案】62°;
类型三、线段的垂直平分线的应用
/4、(2019?上城区校级模拟)数学来源于生活又服务于生活,利用数学中的几何知识可以帮助我们解决许多实际问题.李明准备与朋友合伙经营一个超市,经调查发现他家附近有两个大的居民区A、B,同时又有相交的两条公路,李明想把超市建在到两居民区的距离、到两公路距离分别相等的位置上,绘制了如下的居民区和公路的位置图.聪明的你一定能用所学的数学知识帮助李明在图上确定超市的位置!请用尺规作图确定超市P的位置.(作图不写作法,但要求保留作图痕迹.)
/
【思路点拨】先画角的平分线,再画出线段AB的垂直平分线,两线的交点就是P.
【答案与解析】
解:
/
【总结升华】本题考查了角的平分线、线段垂直平分线的性质.
【巩固练习】
一.选择题
1.(2019?漳州)下列图案属于轴对称图形的是( )
A./ B./ C./ D./
2.如图,ΔABC与Δ/关于直线/对称,则∠B的度数为 ( )
/
A.30° B.50° C.90° D.100°
3. 下列说法中错误的是( )
A.两个对称的图形对应点连线的垂直平分线就是它们的对称轴
B.关于某直线对称的两个图形全等
C.面积相等的两个三角形对称
D.轴对称指的是两个图形沿着某一直线对折后重合
4.(2019春?高密市校级月考)已知,如图,点P关于OA、OB的对称点分别是P1,P2,线段P1P2分别交OA、OB于D、C,P1P2=6cm,则△PCD的周长为( )
/
A.3cm B.6cm C.12cm D.无法确定
5. 如图,有A、B、C三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )
A.在AC,BC两边高线的交点处 B.在AC,BC两边中线的交点处
C.在AC,BC两边垂直平分线的交点处 D.在∠A,∠B两内角平分线的交点处
/
6.如图所示,BE⊥AC于点D,且AD=CD,BD=ED,若∠ABC=54°,则∠E=( ).
A.25° B.27° C.30° D.45°
/
二.填空题
7. ΔABC中,若AB-AC=2/,BC的垂直平分线交AB于D点,且ΔACD的周长为14/,则AB=_____,AC=_____.
8.如图,ΔABC中,AB=AC,AB的垂直平分线交AC于P点.
(1)若∠A=35°,则∠BPC=_____;
(2)若AB=5/,BC=3/,则ΔPBC的周长=_____cm.
/
9.(2019秋?淮北期末)数学在我们的生活中无处不在,就连小小的台球桌上都有数学问题.如图所示,∠1=∠2,若∠3=30°,为了使白球反弹后能将黑球直接撞入袋中,那么击打白球时,必须保证∠1等于 .
/
10.如图,CD与BE互相垂直平分,AD⊥DB,∠BDE=70°,则∠CAD=______°.
/
11. 如图,在△ABC中,∠C=90°,AB的垂直平分线MN分别交AC,AB于点D,E. 若∠CBD : ∠DBA =3:1,则∠A的度数为________.
/
12.(2019?丰台区二模)如图,在棋盘中建立直角坐标系xOy,三颗棋子A,O,B的位置分别是(﹣1,1),(0,0)和(1,0).如果在其他格点位置添加一颗棋子C,使A,O,B,C四颗棋子成为一个轴对称图形,请写出所有满足条件的棋子C的位置的坐标: .
/
三.解答题
13. 如图所示,一个算式在镜中所成的像构成的算式是正确的,但是在实际中是正确的吗?实际中这个算式是什么?
/
14. 如图所示,△ABC中,AB>AC,∠BAC的平分线与BC的垂直平分线DM相交于D,过D作DE⊥AB于E,作DF⊥AC于F,求证:BE=CF.
/
15.(2019?黄岛区校级模拟)某公园有海盗船、摩天轮、碰碰车三个娱乐项目,现要在公园内建一个售票中心,使得三个娱乐项目所处位置到售票中心的距离相等,请在图中确定售票中心的位置.
/
【答案与解析】
一.选择题
1. 【答案】A;
【解析】根据轴对称图形的定义判断.
2. 【答案】D;
【解析】成轴对称的两个图形对应线段、对应角相等.
3. 【答案】C;
【解析】面积相等不一定全等,也不一定对称.
4. 【答案】B;
【解析】解:∵点P关于OA、OB的对称点分别是P1,P2,
∴PD=P1D,PC=P2C;
∵P1P2=6(cm),
∴P1D+DC+P2C=6(cm),
∴PD+DC+PC=6(cm),
即△PCD的周长为6cm.
故选:B.
5. 【答案】C;
【解析】三角形垂直平分线的交点到三个顶点的距离相等.
6. 【答案】B;
【解析】AC,BD互为对方的中垂线,∠ABD=∠CBD=∠E=54°÷2=27°.
二.填空题
7. 【答案】8cm, 6cm;
【解析】由题意,BD=CD,AB-AC=2,AB+AC=14,解得AB=8;AC=6.
8. 【答案】70, 8;
【解析】由垂直平分线的性质,AP=BP,∠A=∠ABP=35°,∠BPA=110°,
∠BPC=70°.ΔPBC的周长=BP+PC+BC= AP+PC+BC=5+3=8/.
9. 【答案】60°;
【解析】解:∵由题意可得:∠2+∠3=90°,∠3=30°,
∴∠2=60°,
∵∠1=∠2,
∴∠1=60°.
故答案为:60°.
10.【答案】70;
【解析】∵CD与BE互相垂直平分,∴DB=DE,∵∠BDE=70°,∴∠BDC=35°,∠ABD=55°,∵AD⊥DB,∴∠BAD=90°-55°=35°,根据轴对称性,四边形ACBD关于直线AB成轴对称,∴∠CAD=∠BAC+∠BAD=35°+35°=70°.
11.【答案】18°;
【解析】∠A=∠ABD=/,∠CBD=3/,5/=90°,/=18°.
12.【答案】(﹣1,2),(2,1),(﹣1,﹣1),(0.﹣1);
【解析】如图所示,C点的位置为(﹣1,2),(2,1),A,O,B,C四颗棋子组成等腰梯形,直线l为该图形的对称轴,C点的位置为(﹣1,﹣1),x轴是对称轴,C点的位置为(0.﹣1),故答案为:(﹣1,2),(2,1),(﹣1,﹣1),(0.﹣1).
/
三.解答题
13.【解析】
在实际中的算式是:151+25+12=188;结果也是正确的.
14.【解析】
证明:连接BD、CD, ∵AD是∠BAC的平分线,DE⊥AB,DF⊥AC, ∴DE=DF(角平分线上的点到角的两边距离相等). ∵MD是BC的垂直平分线, ∴DB=DC(线段垂直平分线上的点到线段两个端点的距离相等). ∴Rt△DEB≌Rt△DFC(HL). ∴BE=CF(全等三角形对应边相等).
15.【解析】
解:如图,①连接AB,AC,
②分别作线段AB,AC的垂直平分线,两垂直平分线相较于点P,
则P即为售票中心.
/
【学习目标】
1.理解轴对称图形以及两个图形成轴对称的概念,弄清它们之间的区别与联系,能识别轴对称图形.
2.理解图形成轴对称的性质,会画一些简单的关于某直线对称的图形.
3.理解线段的垂直平分线的概念,掌握线段的垂直平分线的性质及判定,会画已知线段的垂直平分线.
4.能运用线段的垂直平分线的性质解决简单的数学问题及实际问题.
【要点梳理】
【 轴对称 知识要点】
要点一、轴对称图形 轴对称图形的定义
一个图形沿着某直线折叠,直线两旁的部分能完全重合,这个图形就叫做轴对称图形,该直线就是它的对称轴.
要点诠释: 轴对称图形是指一个图形,图形被对称轴分成的两部分能够互相重合.一个轴对称图形的对称轴不一定只有一条,也可能有两条或多条,因图形而定. 要点二、轴对称 1.轴对称定义
把一个图形沿着某一条直线折叠,如果它能够与另一个图形重合,那么就说这两个图形关于这条直线对称(或说这两个图形成轴对称),这条直线叫做对称轴.折叠后重合的点是对应点,也叫做对称点 要点诠释: 轴对称指的是两个图形的位置关系,两个图形沿着某条直线对折后能够完全重合.成轴对称的两个图形一定全等.
2.轴对称与轴对称图形的区别与联系
轴对称与轴对称图形的区别主要是:轴对称是指两个图形,而轴对称图形是一个图形;轴对称图形和轴对称的关系非常密切,若把成轴对称的两个图形看作一个整体,则这个整体就是轴对称图形;反过来,若把轴对称图形的对称轴两旁的部分看作两个图形,则这两个图形关于这条直线(原对称轴)对称.
要点三、轴对称与轴对称图形的性质
轴对称、轴对称图形的性质 轴对称的性质:若两个图形关于某直线对称,那么对称轴是任何一对对应点所连线段的垂直平分线;
轴对称图形的性质:轴对称图形的对称轴也是任何一对对应点所连线段的垂直平分线.
要点四、线段的垂直平分线
定义:
经过线段中点并且垂直于这条线段的直线,叫做这条线段的垂直平分线,也叫线段的中垂线.
性质:
性质1:线段垂直平分线上的点到线段两端点的距离相等; 性质2:与一条线段两个端点距离相等的点在这条线段的垂直平分线上.
要点诠释:
线段的垂直平分线的性质是证明两线段相等的常用方法之一.同时也给出了引辅助线的方法,那就是遇见线段的垂直平分线,画出到线段两个端点的距离,这样就出现相等线段,直接或间接地为构造全等三角形创造条件.
三角形三边垂直平分线交于一点,该点到三角形三顶点的距离相等,这点是三角形外接圆的圆心——外心.
【典型例题】
类型一、判断轴对称图形
/1、(2019?邵阳)下面四个手机应用图标中是轴对称图形的是( )
A./ B./ C./ D./
【思路点拨】我们将图中的图形分别沿着某条直线对折,看看图形的两边能否重合,若重合则是轴对称图形,否则就不是.
【答案】D;
【解析】轴对称图形即能找到对称轴,使对称轴两边的图形重合.
【总结升华】找对称轴要注意从不同的角度去观察,做到不重复、不遗漏.
举一反三:
【变式】(2019春?太谷县校级期末)将一张矩形的纸对折,然后用笔尖在上面扎出“B”,再把它铺平,你可见到( )
A./ B./ C./ D./
【答案】C.
【 轴对称 例2】
/2、将一个正方形纸片依次按图/的方式对折,然后沿图/中的虚线裁剪,成图/样式,将纸展开铺平,所得到的图形是图中的 ( )
/
/
【答案】D;
【解析】/
【总结升华】只需要根据对称轴补全图形就能找到答案.
举一反三:
【变式】将一等腰直角三角形纸片对折后再对折,得到如图所示的图形,然后将阴影部分剪掉,把剩余部分展开后的平面图形是( )
/
【答案】A;
类型二、轴对称或轴对称图形的应用
【 轴对称 例3】
/3、如图,将矩形纸片ABCD (图①)按如下步骤操作:(1)以过点A的直线为折痕折叠纸片,使点B恰好落在AD边上,折痕与BC边交于点E (如图②);(2)以过点E的直线为折痕折叠纸片,使点A落在BC边上,折痕EF交AD边于点F (如图③); (3)将纸片收展平,那么∠AEF的度数为( )
/
A.60° B.67.5° C.72° D.75°
【答案】B;
【解析】∠AEF=(180°-45°)÷2=67.5°.
【总结升华】折叠所形成的图形是轴对称图形,对应角相等.
举一反三:
【变式1】如图,△ABC中,AB=BC,△ABC沿DE折叠后,点A落在BC边上的/处,若点D为AB边的中点,∠A=70°,求∠BD/的度数.
/
【答案】100°;
∵AB=BC,
∴∠A=∠C=70°,∠B=40°
又∵ΔABC沿DE折叠后,点A落在BC边上的/处,点D为AB边的中点,
∴BD=D/,∠B=∠D/B=40°,
∴∠BD/=180°-40°-40°=100°.
【变式2】将矩形ABCD沿AE折叠,得到如图所示图形. 若/=56°,则∠AED的大小是_______.
/
【答案】62°;
类型三、线段的垂直平分线的应用
/4、(2019?上城区校级模拟)数学来源于生活又服务于生活,利用数学中的几何知识可以帮助我们解决许多实际问题.李明准备与朋友合伙经营一个超市,经调查发现他家附近有两个大的居民区A、B,同时又有相交的两条公路,李明想把超市建在到两居民区的距离、到两公路距离分别相等的位置上,绘制了如下的居民区和公路的位置图.聪明的你一定能用所学的数学知识帮助李明在图上确定超市的位置!请用尺规作图确定超市P的位置.(作图不写作法,但要求保留作图痕迹.)
/
【思路点拨】先画角的平分线,再画出线段AB的垂直平分线,两线的交点就是P.
【答案与解析】
解:
/
【总结升华】本题考查了角的平分线、线段垂直平分线的性质.
【巩固练习】
一.选择题
1.(2019?漳州)下列图案属于轴对称图形的是( )
A./ B./ C./ D./
2.如图,ΔABC与Δ/关于直线/对称,则∠B的度数为 ( )
/
A.30° B.50° C.90° D.100°
3. 下列说法中错误的是( )
A.两个对称的图形对应点连线的垂直平分线就是它们的对称轴
B.关于某直线对称的两个图形全等
C.面积相等的两个三角形对称
D.轴对称指的是两个图形沿着某一直线对折后重合
4.(2019春?高密市校级月考)已知,如图,点P关于OA、OB的对称点分别是P1,P2,线段P1P2分别交OA、OB于D、C,P1P2=6cm,则△PCD的周长为( )
/
A.3cm B.6cm C.12cm D.无法确定
5. 如图,有A、B、C三个居民小区的位置成三角形,现决定在三个小区之间修建一个购物超市,使超市到三个小区的距离相等,则超市应建在( )
A.在AC,BC两边高线的交点处 B.在AC,BC两边中线的交点处
C.在AC,BC两边垂直平分线的交点处 D.在∠A,∠B两内角平分线的交点处
/
6.如图所示,BE⊥AC于点D,且AD=CD,BD=ED,若∠ABC=54°,则∠E=( ).
A.25° B.27° C.30° D.45°
/
二.填空题
7. ΔABC中,若AB-AC=2/,BC的垂直平分线交AB于D点,且ΔACD的周长为14/,则AB=_____,AC=_____.
8.如图,ΔABC中,AB=AC,AB的垂直平分线交AC于P点.
(1)若∠A=35°,则∠BPC=_____;
(2)若AB=5/,BC=3/,则ΔPBC的周长=_____cm.
/
9.(2019秋?淮北期末)数学在我们的生活中无处不在,就连小小的台球桌上都有数学问题.如图所示,∠1=∠2,若∠3=30°,为了使白球反弹后能将黑球直接撞入袋中,那么击打白球时,必须保证∠1等于 .
/
10.如图,CD与BE互相垂直平分,AD⊥DB,∠BDE=70°,则∠CAD=______°.
/
11. 如图,在△ABC中,∠C=90°,AB的垂直平分线MN分别交AC,AB于点D,E. 若∠CBD : ∠DBA =3:1,则∠A的度数为________.
/
12.(2019?丰台区二模)如图,在棋盘中建立直角坐标系xOy,三颗棋子A,O,B的位置分别是(﹣1,1),(0,0)和(1,0).如果在其他格点位置添加一颗棋子C,使A,O,B,C四颗棋子成为一个轴对称图形,请写出所有满足条件的棋子C的位置的坐标: .
/
三.解答题
13. 如图所示,一个算式在镜中所成的像构成的算式是正确的,但是在实际中是正确的吗?实际中这个算式是什么?
/
14. 如图所示,△ABC中,AB>AC,∠BAC的平分线与BC的垂直平分线DM相交于D,过D作DE⊥AB于E,作DF⊥AC于F,求证:BE=CF.
/
15.(2019?黄岛区校级模拟)某公园有海盗船、摩天轮、碰碰车三个娱乐项目,现要在公园内建一个售票中心,使得三个娱乐项目所处位置到售票中心的距离相等,请在图中确定售票中心的位置.
/
【答案与解析】
一.选择题
1. 【答案】A;
【解析】根据轴对称图形的定义判断.
2. 【答案】D;
【解析】成轴对称的两个图形对应线段、对应角相等.
3. 【答案】C;
【解析】面积相等不一定全等,也不一定对称.
4. 【答案】B;
【解析】解:∵点P关于OA、OB的对称点分别是P1,P2,
∴PD=P1D,PC=P2C;
∵P1P2=6(cm),
∴P1D+DC+P2C=6(cm),
∴PD+DC+PC=6(cm),
即△PCD的周长为6cm.
故选:B.
5. 【答案】C;
【解析】三角形垂直平分线的交点到三个顶点的距离相等.
6. 【答案】B;
【解析】AC,BD互为对方的中垂线,∠ABD=∠CBD=∠E=54°÷2=27°.
二.填空题
7. 【答案】8cm, 6cm;
【解析】由题意,BD=CD,AB-AC=2,AB+AC=14,解得AB=8;AC=6.
8. 【答案】70, 8;
【解析】由垂直平分线的性质,AP=BP,∠A=∠ABP=35°,∠BPA=110°,
∠BPC=70°.ΔPBC的周长=BP+PC+BC= AP+PC+BC=5+3=8/.
9. 【答案】60°;
【解析】解:∵由题意可得:∠2+∠3=90°,∠3=30°,
∴∠2=60°,
∵∠1=∠2,
∴∠1=60°.
故答案为:60°.
10.【答案】70;
【解析】∵CD与BE互相垂直平分,∴DB=DE,∵∠BDE=70°,∴∠BDC=35°,∠ABD=55°,∵AD⊥DB,∴∠BAD=90°-55°=35°,根据轴对称性,四边形ACBD关于直线AB成轴对称,∴∠CAD=∠BAC+∠BAD=35°+35°=70°.
11.【答案】18°;
【解析】∠A=∠ABD=/,∠CBD=3/,5/=90°,/=18°.
12.【答案】(﹣1,2),(2,1),(﹣1,﹣1),(0.﹣1);
【解析】如图所示,C点的位置为(﹣1,2),(2,1),A,O,B,C四颗棋子组成等腰梯形,直线l为该图形的对称轴,C点的位置为(﹣1,﹣1),x轴是对称轴,C点的位置为(0.﹣1),故答案为:(﹣1,2),(2,1),(﹣1,﹣1),(0.﹣1).
/
三.解答题
13.【解析】
在实际中的算式是:151+25+12=188;结果也是正确的.
14.【解析】
证明:连接BD、CD, ∵AD是∠BAC的平分线,DE⊥AB,DF⊥AC, ∴DE=DF(角平分线上的点到角的两边距离相等). ∵MD是BC的垂直平分线, ∴DB=DC(线段垂直平分线上的点到线段两个端点的距离相等). ∴Rt△DEB≌Rt△DFC(HL). ∴BE=CF(全等三角形对应边相等).
15.【解析】
解:如图,①连接AB,AC,
②分别作线段AB,AC的垂直平分线,两垂直平分线相较于点P,
则P即为售票中心.
/
